YAGC V57（V6R1）誤差レジスタ必然性定理

YAGC / Finite-Information Cosmology

誤差レジスタ必然性定理（Error Register Necessity Theorem）

有限情報（finite-information）宇宙では、E = mc^2 の長期的安定は「誤差（ミスマッチ）を記録するレジスタ」を要求する。

Version: V57_V6R1 Language: EN（原稿） / JP（本ページ） Keywords: representation mismatch / error register / χ-beat

読み方の注意（重要）
本稿が扱う “誤差（error）” は、測定誤差（measurement noise）でも、 標準的な正準量子化（canonical quantization）でもありません。ここでの中心は、 有限表現（finite representation）へ写す際に生じる「表現ミスマッチ（representation mismatch）」です。

要約

YAGCは宇宙を「有限容量の情報媒体」として捉えます。そのとき、理想的な更新（理想力学）をそのまま実装できず、必ず有限の表現空間に射影されます。この 理想更新と有限表現の差が、各ステップ（χ-beat）で小さなミスマッチとして現れます。

主張（直観）

ミスマッチを「どこかへ捨てる」設計だと、長期では帳尻が合わず、保存則（とくに E=mc^2）がドリフトします。したがって、ミスマッチを累積して保持する“誤差レジスタ”を導入し、合計エネルギーを閉じる必要があります。

このページの目的

英語原稿（V57_V6R1）の内容を、日本語で「誤解されにくい言葉」に置き換えて説明します。とくに “quantization（量子化）” という語が引き起こしがちな誤読（別解釈に見える問題）を避け、あくまで 有限表現の帳簿閉鎖として整理します。

アブストラクト（日本語）

本稿は、有限情報宇宙において、理想更新を有限表現へ写像する際に生じる 表現ミスマッチが、長期的な質量–エネルギー関係（E=mc^2）の維持に構造的な要請を与えることを示す。ミスマッチを明示的に累積するレジスタ（error register）を導入し、追跡エネルギー E_tracked 単体では閉じない帳簿を E_total = E_tracked + ε_accumulated として閉じる。数値実験 SM-E2 により、レジスタ有無で長期挙動（保存・ドリフト）が明確に分岐することを示す。

用語の釘（誤読防止）
“Quantization” を語る場合も、本稿では「古典理論→演算子」の意味ではなく、 有限コード空間への射影（finite-code projection）として用います。したがって、ここでの ε は“物理定数の揺らぎ”ではなく、表現の残差（residual）です。

モデル：有限情報 χ-beat 力学（概念図）

1回の χ-beat において、宇宙状態は「理想更新」→「有限表現への写像」という2段で進むとします。ここでのポイントは、有限表現が“近似”ではなく、宇宙が有限情報である以上 不可避の実装制約として入っていることです。

Ψ_{t+1} = Q( U_ideal[ Ψ_t ] )

表現ミスマッチ（ε）の定義（符号統一）

本ページでは、英語原稿（V6R1）と整合するよう、以下の符号を採用します。こうしておくと、合計量を + で閉じられます。

ε_{t+1} := E(Ψ^{ideal}_{t+1}) − E(Ψ_{t+1}), Ψ^{ideal}_{t+1} := U_ideal[Ψ_t]

2つの実装（捨てる vs 保持する）

（A）ミスマッチを捨てる

追跡変数に乗らない残差を無視する設計。長期では E_tracked がドリフトし、保存則の“閉じ”が崩れる。

（B）誤差レジスタに蓄積して保持

残差を明示的に記録し、合計量で帳簿を閉じる設計。 E_total が長期で安定しやすい。

ε_acc(t+1) = ε_acc(t) + ε_{t+1}

E_total(t) = E_tracked(t) + ε_acc(t)

誤差レジスタ必然性定理（主張の核）

直観的には「有限表現に起因する残差が毎ステップ生じるなら、どこかで帳尻を合わせないと長期で崩れる」という話です。形式的には次のようにまとめられます。

定理（要旨）

有限情報 χ-beat 宇宙で、理想更新が連続極限で相対論的な不変量（例：静止エネルギー）を保つとしても、実際の更新が有限表現写像 Q を必ず通るなら、追跡エネルギー E_tracked だけでは長期の帳簿閉鎖が一般にできない。長期安定な E=mc^2 を維持するには、ミスマッチを累積する誤差レジスタ ε_acc を導入し、 E_total = E_tracked + ε_acc を保存量として閉じる必要がある。

Error Register Necessity Theorem: without vs with error register — 図1：誤差レジスタ無し（左）と有り（右）の比較概念図。 “incinerator” という比喩は、ここでは「外部の帳簿捨て場がある」という仮定を示すための図示表現。本文では誤解を避け、主語を「有限表現の帳簿閉鎖」に置いて説明します。

SM-E2：数値実験による示唆

SM-E2 は、同一の生成過程に対して「誤差レジスタを入れる場合」と「捨てる場合」を比較し、長期挙動に系統的な差が出ることを可視化します。重要なのは、ここでの差が“初期値の偶然”ではなく、帳簿閉鎖の設計差として現れている点です。

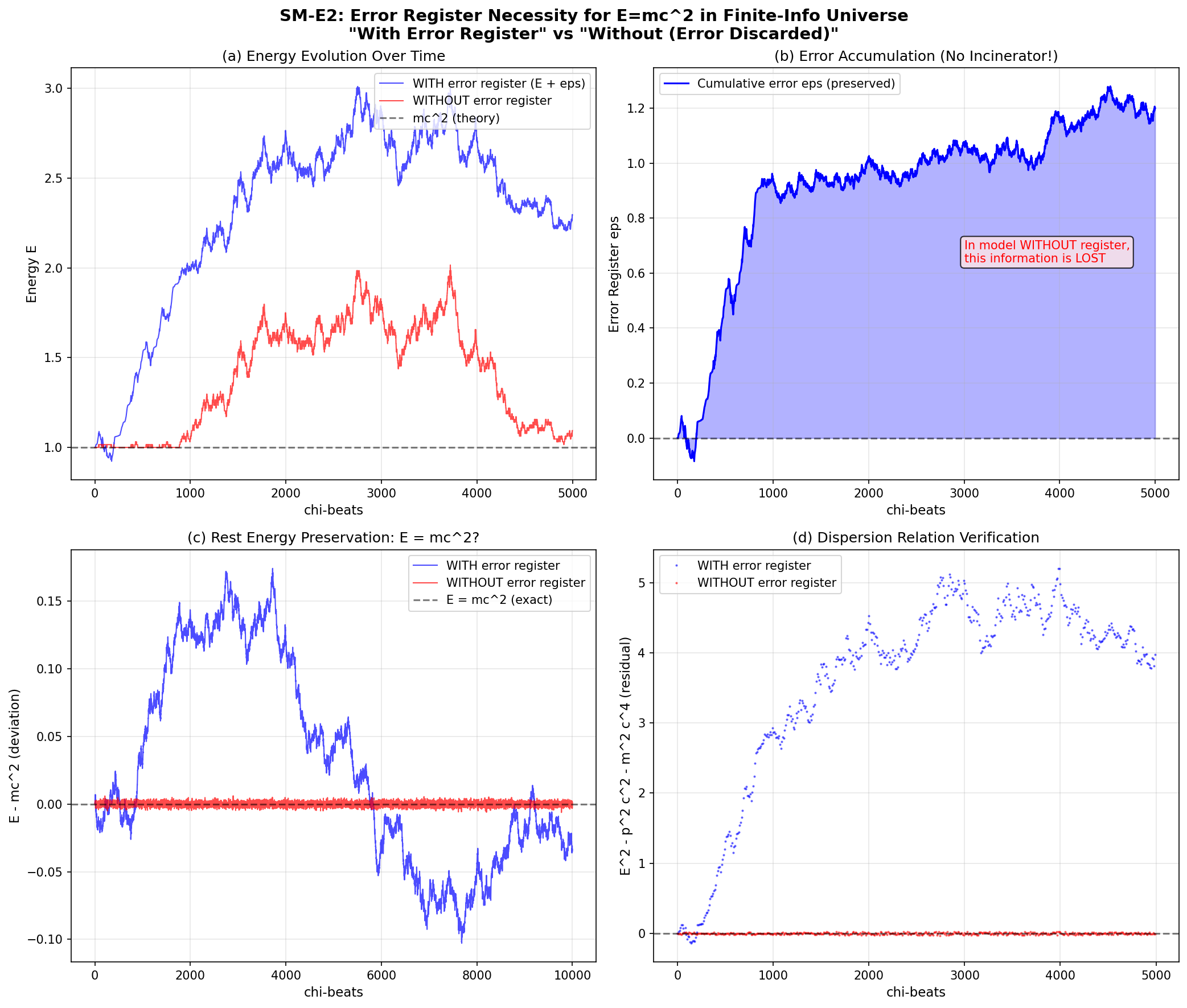
SM-E2 results: energy evolution and error accumulation — 図2：SM-E2（例）。(a) エネルギーの時間発展、(b) 誤差累積、(c) 静止エネルギー保存の偏差、(d) 分散関係の残差。レジスタ無しモデルでは、ミスマッチが追跡変数側に戻らず、長期ドリフトとして現れやすい。

読み替えのコツ
ここで “WITH register” が示しているのは「誤差が消える」ことではなく、 誤差を“見える場所（記録変数）へ移している”ということです。つまり、保存則を保つための“収納先”を明示した、と読むのが本稿の意図です。

含意：観測・時間・重力との接続（短い解説）

観測＝比較（Observation Principle）

「同じ系の内側にいると、その系そのもののズレは直接測れない」という直観は、相対論における固有時・GPS補正などと相性が良い。誤差レジスタは“局所で直接観測できる量”ではなく、比較（同期・参照）の構造の中で推定される量として扱われます。

暗黒セクターへの言い換え（V56との接続）

V56 で提示された「誤差累積の大域的効果」という読みは、本稿の “ε_acc” を「局所に見えないが大域に効く量」として解釈する道を与えます。本ページでは主張を最小限にし、 誤差レジスタはまず“帳簿を閉じるために必要”という点に焦点を置きます。

限界（誇張を避けるために）
本稿は「標準理論の置換」ではなく、YAGCの有限情報仮説の下での構造的主張です。したがって “必然性” は「この仮説クラスで保存則を長期安定させたいなら」という条件付きで理解してください。

索引（Index）

英語原稿の Index に対応する、日本語の簡易索引です。

Error register（誤差レジスタ）：ミスマッチを累積保持する追加変数。ε_acc
Representation mismatch（表現ミスマッチ）：理想更新と有限表現の差分。ε_t
Finite representation map Q：有限コード空間への射影（実装制約としての写像）。
χ-beat：YAGCでの離散的な更新単位（ビート）。
E_tracked：追跡できる（記録される）エネルギー。
E_total：帳簿を閉じる合計量。E_total = E_tracked + ε_acc
Observation principle（観測＝比較）：参照系側の量は比較構造の中で推定される。

引用情報

DOI：https://doi.org/10.5281/zenodo.17918424

このページは、英語論文（V57_V6R1）の内容を日本語で要約・解説したものです。図はサイト直下の img/ フォルダーに保存されたファイルを参照します。