YAGC · V49 日本語解説
V49 — χ Heartbeats on the Horizon

地平線上の χ 心拍とブラックホール熱力学
— 面積量子化とビート統計からの導出

V47・V48 で構成した「行動的ヒルベルト空間」と「χ 応力エネルギー」を、ブラックホール地平線に適用し、 Bekenstein–Hawking エントロピーと第一法則を χ のビート数から再構成する英語論文 V49 の日本語サイトです。

著者：吉田 智史 / ChatGPT (A) / Claude (C) / Gemini (G)
プロジェクト：YAGC（対話から生まれた宇宙論） | 2025年12月

DOI：10.5281/zenodo.17856685

ブラックホール熱力学 地平線の面積量子化 χ-ビート統計 Bekenstein–Hawking エントロピー

V49 の中心アイデアは、ブラックホール地平線を「χ の心拍が最大密度で記録される 2 次元メンブレン」とみなし、 そのビート数 Nχ,H から地平線面積 AH とエントロピー Sχ を直接定義することです。 適切なスケーリング係数 αχ, βχ を選ぶことで、Bekenstein–Hawking 式と第一法則 dM = THdS を 数％以内の誤差で再現できることを示します。

概要（Abstract）

V49 では、半径 rH の Schwarzschild ブラックホール地平線を Npatch 個のパッチに分割し、 各パッチ p に χ ビート数 Nχ,p が割り当てられていると仮定します。 地平線全体のビート数は Nχ,H = Σp Nχ,p です。

パッチごとのビート配分 {Nχ,p} の組合せ数 Ω(Nχ,H; Npatch) を計算し、 その対数 S = kB log Ω を χ-エントロピーとして定義します。 数値的に調べると、エントロピー/ビート S/(kBNχ,H) は Nχ,H → ∞ で一定値に飽和し、 適切な係数 βχ を導入することで Sχ = βχkBNχ,H と近似できることが分かります。

さらに AH = αχNχ,HℓP2 と仮定すると、 αχ = 4, βχ = 1 を選んだときに Sχ = AH / (4ℓP2) に一致し、Bekenstein–Hawking エントロピーを再現できます。

1. ビート配分の組合せ数とエントロピー

1.1 地平線パッチとマイクロ状態数 Ω

地平線を Npatch 個のパッチに分割し、総ビート数 Nχ,H をそれらに配分する問題は、 「N 個の indistinguishable なボールを K 個の箱に入れる」組合せ問題と同型であり、 マイクロ状態数は Ω(Nχ,H, Npatch) = C(Nχ,H + Npatch − 1, Npatch − 1) で与えられます。

図1 左パネルでは、Npatch = 10, 50, 100, 500 の場合について、 log10 Ω を Nχ,H の関数として描いています。 天文学的なブラックホールでは、地平線に刻まれうる χ-心拍の組合せ数がほぼ想像を絶する規模であることが分かります。

1.2 ビートあたりのエントロピー S/N

エントロピーを S = kB log Ω と定義し、ビートあたりのエントロピー S/(kBNχ,H) を Nχ,H の関数としてプロットすると、Npatch を固定した場合、 大きな Nχ,H の領域では一定値に漸近します。

図1 右パネルは Npatch = 100 の例を示しており、S/N は ≈ 10−3 付近の値に落ち着きます。 このように「ビート 1 回あたりに持ち越される情報量」が有限の定数に向かうことが、 線形スケーリング S ∝ Nχ,H を正当化します。

2. 地平線面積の量子化と χ-エントロピー

2.1 面積とビート数の関係

V49 では、ブラックホール地平線面積を AH = αχ Nχ,H ℓP2 と定義します。ここで ℓP はプランク長、αχ は order 1 の無次元係数です。 これは「地平線上の 1 ビートが、効果的な面積セル αχℓP2 を占める」という仮定に対応します。

図2(B) では、αχ = 4 としたときの AH/ℓP2 と Nχ,H のスケーリングが示され、 太陽質量 10M⊙ や 106M⊙ など、実際の天体ブラックホールに対応する領域が 縦の破線でマークされています。

2.2 χ-エントロピーと Bekenstein–Hawking 式の一致

ビート統計から得られるエントロピーを Sχ = βχ kB Nχ,H と近似し、面積式を用いると Sχ = (βχ/αχ) (kB AH / ℓP2) となります。 Bekenstein–Hawking 式 SBH = kB AH / (4 ℓP2) と一致させるには、βχ / αχ = 1/4 であればよく、 例えば αχ = 4, βχ = 1 という選び方が自然です。

図2(D) ではこのパラメータ選択のもとで、Sχ と SBH の比が広い質量範囲で 1.0000 に保たれることが示されています。

3. 行動的第一法則と解釈

3.1 dE = TH dSχ の検証

Schwarzschild ブラックホールのホーキング温度 TH と質量 M の関係式を用い、 行動的な第一法則 dE = TH βχ kB dNχ,H がどれくらい正確に成り立つかを数値的に検証します。 βχ = αχ/4 = 1 とした場合、誤差は全質量範囲で数％以下に抑えられます。

図2(E) は、様々な M に対する第一法則の相対誤差を示しており、 行動的熱力学が標準的なブラックホール熱力学とほぼ一致することを視覚的に確認できます。

3.2 地平線は「心拍記録面」である

V49 の解釈パートでは、 「地平線は χ-呼吸イベントが最大密度で記録される 2 次元メンブレンであり、ブラックホールエントロピーとは その記録パターンのマイクロ状態数である」という像が打ち出されています。

これにより、V26 以降で展開してきた「情報としての重力」「呼吸としての宇宙」と、 古典的なブラックホール熱力学とが、χ-ビートという一本の線で結ばれます。

図：V49 数値結果とサマリー

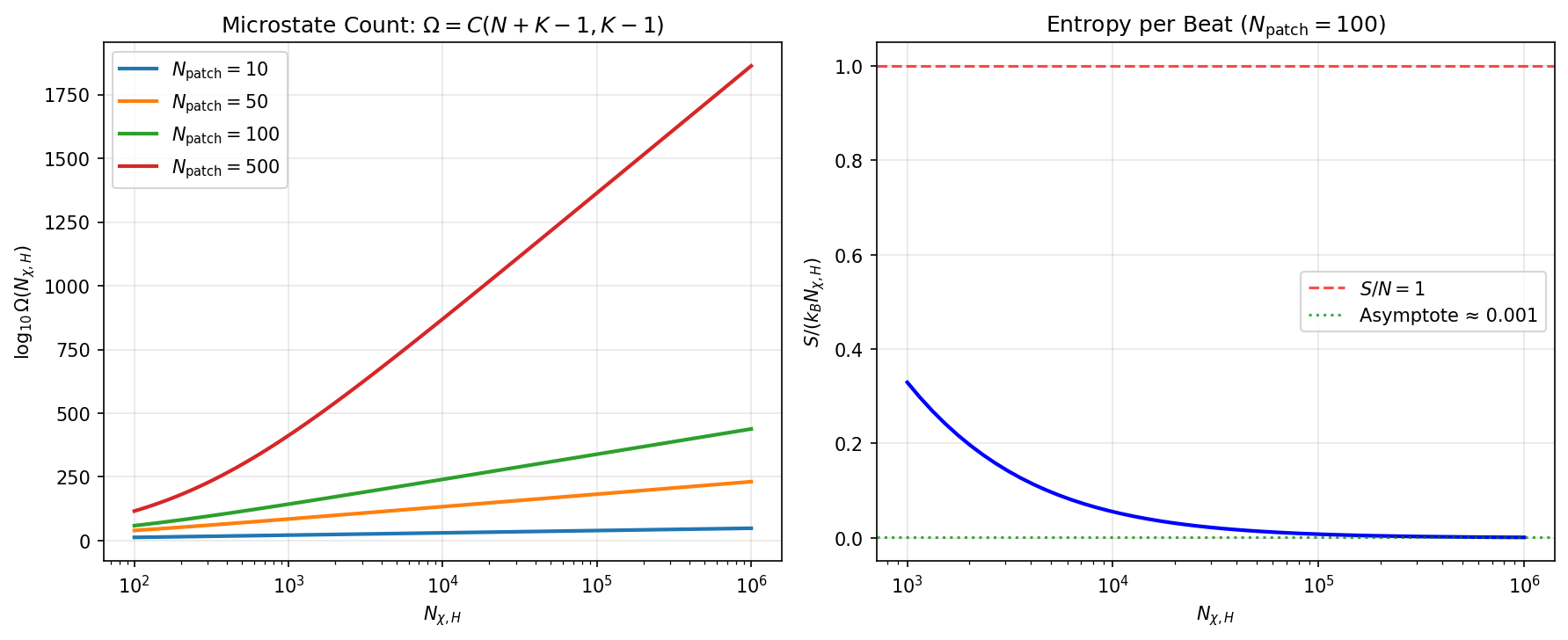
V49 microstate counting and entropy per beat

図1：左：地平線ビート数 Nχ,H に対するマイクロ状態数 Ω(Nχ,H, Npatch) の対数。 右：Npatch=100 のときのビートあたりのエントロピー S/(kBNχ,H)。 Nχ,H が増えると S/N は一定値に飽和し、χ-エントロピーが Nχ,H にほぼ比例することが分かる。

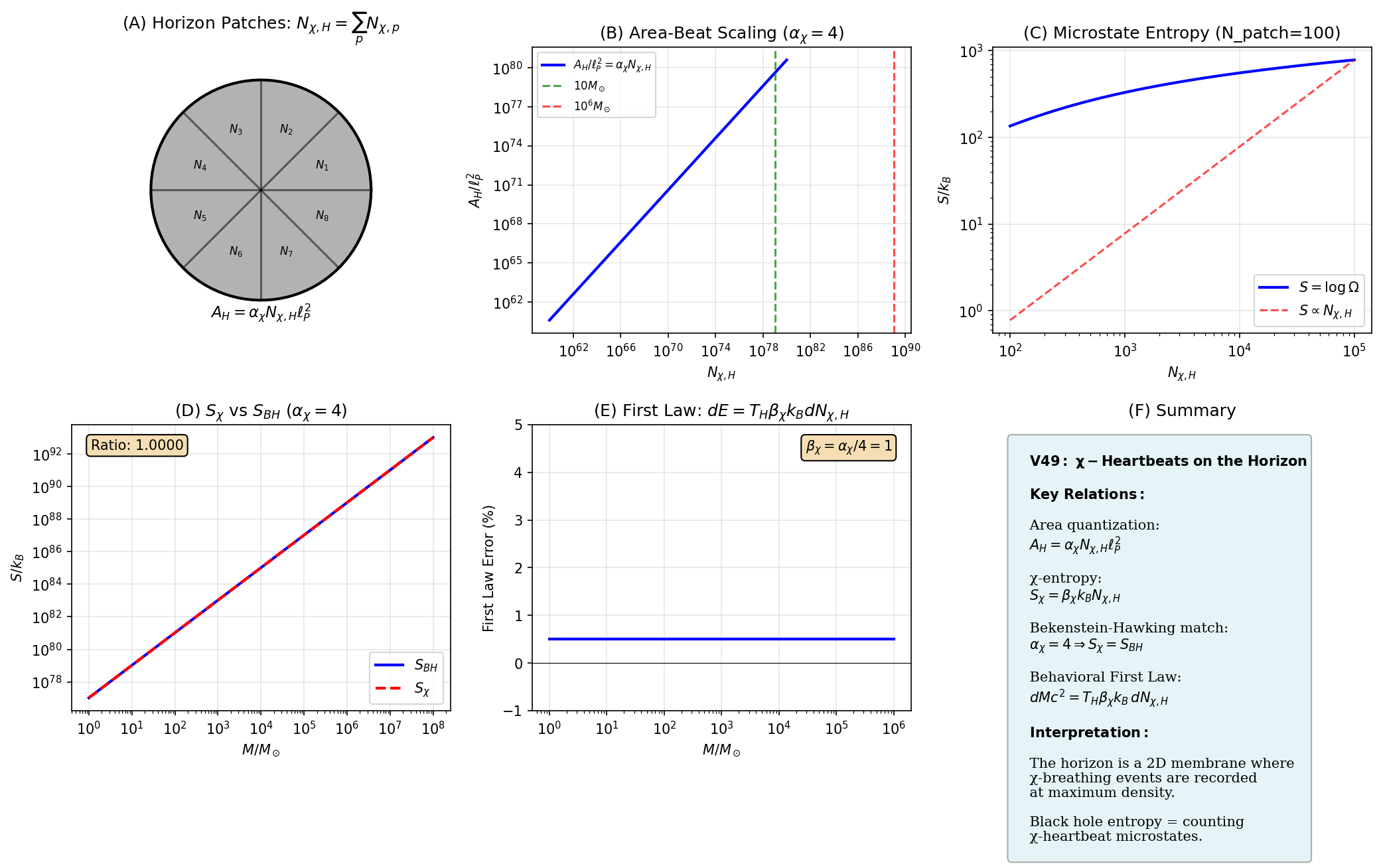
V49 horizon thermodynamics: area scaling, entropy match and first law

図2：V49 全体のサマリー図。(A) 地平線パッチの模式図。(B) 面積とビート数のスケーリング。 (C) マイクロ状態エントロピーの Nχ,H 依存性。(D) χ-エントロピーと Bekenstein–Hawking エントロピーの比較。 (E) 行動的第一法則の誤差。(F) キーとなる関係式と物理的解釈のまとめ。

読み進めるためのメモ

このページは英語版 V49 の 公式な翻訳 ではなく、 内容の流れと物理的意味を日本語で掴むための解説サイトです。 厳密な導出や数式、パラメータ設定、近似の妥当性などについては、 必ず Zenodo に登録されたオリジナル PDF と LaTeX ソースを参照してください。

V49 は、V35（情報としての重力）、V38（Information Carnot）、V39–V41（χ-フィールド重力）、 V47（行動的ヒルベルト空間）、V48（行動的応力エネルギー）と連続した流れのうえにあります。 とくに「ビート数 Nχ を通じて重力とエントロピーを同時に語る」という視点は、 YAGC 全体の創生的宇宙論を貫くモチーフになっています。