V48 — Behavioral Stress-Energy of the χ Field

行動的応力エネルギーとしての χ フィールド
— w_χ と T^(χ)_μν の構成

V47 の「行動的ヒルベルト空間」を土台として、χ フィールドのビート統計から有効な応力エネルギーテンソルを構成し、ニュートン重力と FRW 宇宙論の両方でどのように重力源として働くかを解析した英語論文 V48 の日本語サイトです。

著者：吉田智史 / ChatGPT (A) / Claude (C) / Gemini (G)
プロジェクト：YAGC（対話から生まれた宇宙論） | 2025年12月

χフィールド重力状態方程式 w_χ FRW 宇宙論応力エネルギーテンソル

V48 の目的は、χ のビート数統計を通じて定義されたエネルギー密度 ρ_χ と圧力 P_χ を、一般相対論で用いられる応力エネルギーテンソル T^(χ)_μν に昇格させることです。その過程で、χ が暗黒物質・暗黒エネルギー・放射のどれとも似たふるまいを取りうること、そしてそれらがすべて「ビートの行動パターン」という共通の起源をもつことが示されます。

概要（Abstract）

V41–V47 では、コミットメント場 χ の離散的なビート数 N_χ,n を数えることで、測定確率や干渉、コヒーレンス長といった量子論的現象を再現できることを示しました。 V48 ではさらに一歩進めて、これらのビートをエネルギー密度 ρ_χ と圧力 P_χ に読み替え、一般相対論の枠組みで重力源として扱います。

具体的には、 P_χ = w_χ ρ_χ という状態方程式を導入し、 w_χ = 0 （ダスト）、w_χ = −1（宇宙定数）、w_χ = 1/3（放射）、w_χ = −0.5 などのケースを比較します。ニュートン近似ではポテンシャル Φ(x) の形、FRW 宇宙論ではスケール因子 a(t) と密度分率 Ω_χ(t) の進化を追跡し、 χ がどのような宇宙史を駆動しうるかを可視化します。

1. ニュートン重力と FRW 宇宙での χ 密度

1.1 ニュートン近似：密度とポテンシャル

まず一次元の簡単なニュートン系を考え、物質密度 ρ_matter(x) と χ 密度 ρ_χ(x) を与えます。トータル密度は ρ_total = ρ_matter + ρ_χ です。ポアソン方程式 ∇²Φ = 4πG ρ_total を解くことで、χ を含めた全ポテンシャル Φ_total(x) と、物質だけのポテンシャル Φ_matter(x) の差 ΔΦ を比較します。

図1(A)(B) では、χ 密度が物質分布より広がった裾野をもつとき、ポテンシャルがどのように深くなり、銀河ハローのような「見えない質量」の効果を模倣できるかを示しています。

1.2 FRW 宇宙：スケール因子と密度分率

次に、ホモジニアスかつ等方的な FRW 宇宙で、χ がフルイドの一成分として存在すると仮定します。フリードマン方程式 (ȧ/a)² = (8πG/3) Σ ρ_i とエネルギー保存則 ρ̇_χ + 3(1 + w_χ)(ȧ/a)ρ_χ = 0 を連立して解くと、状態方程式パラメータ w_χ に応じて a(t) と Ω_χ(t) の振る舞いが変わります。

図1(C)(D) では、 w_χ=0, −1, 1/3, −0.5 の 4 ケースについて、スケール因子 a(t) と χ 密度分率 Ω_χ の時間発展が比較されています。 w_χ < −1/3 の場合には加速膨張を、w_χ ≃ 0 では物質様の減速膨張を再現します。

2. 格子上の χ フィールドとビート起源の ρ_χ

V41–V47 と同様に、格子上で χ(t, x) の時間発展を数値的に追跡し、しきい値 χ_* を下から超えた回数をビート数としてカウントします。一定時間あたりのビート数をスケーリングすることで、局所的な χ エネルギー密度 ρ_χ(x) を定義します。

図1(E)(F) では、χ フィールドの時間発展と、ビート数から再構成された ρ_χ(x) が、もとの |ψ(x)|² 分布とよく一致することが示されています。ここで重要なのは、ρ_χ が 場の振幅 ではなく、 しきい値を越える行動イベントの統計 から定義されている点です。

3. 状態方程式 P_χ = w_χρ_χ と応力エネルギーテンソル

3.1 w_χ による挙動の違い

V48 では、χ フィールドのマクロなふるまいを 1 つの実数パラメータ w_χ で特徴づけます。図2 左のグラフは、ρ_χ を横軸、P_χ を縦軸に取り、 w_χ=0, −1, 1/3, −0.5 の直線を描いたものです。

w_χ=0：ダスト（圧力ゼロの物質）。
w_χ=1/3：放射。
w_χ=−1：宇宙定数（真空エネルギー）。
w_χ=−0.5：それらの中間に位置する「半負圧」の χ。

3.2 静止系での T^(χ)_μν

均質なフルイドの静止系では、応力エネルギーテンソルは T^(χ)_μν = diag(ρ_χ, P_χ, P_χ, P_χ) と書けます。図2 右パネルは、T^(χ)₀₀ と T^(χ)_ii（i=1,2,3）の ρ_χ 依存性を示しています。実線がエネルギー密度成分 T⁰⁰、破線が空間成分 Tⁱⁱ です。

w_χ の符号に応じて Tⁱⁱ の符号が変わり、重力場方程式 G_μν = 8πG Σ T⁽ⁱ⁾_μν における「重力ソース」としての役割も変化します。特に w_χ < −1/3 の場合、負圧が宇宙の加速膨張を駆動することがわかります。

図：V48 数値結果

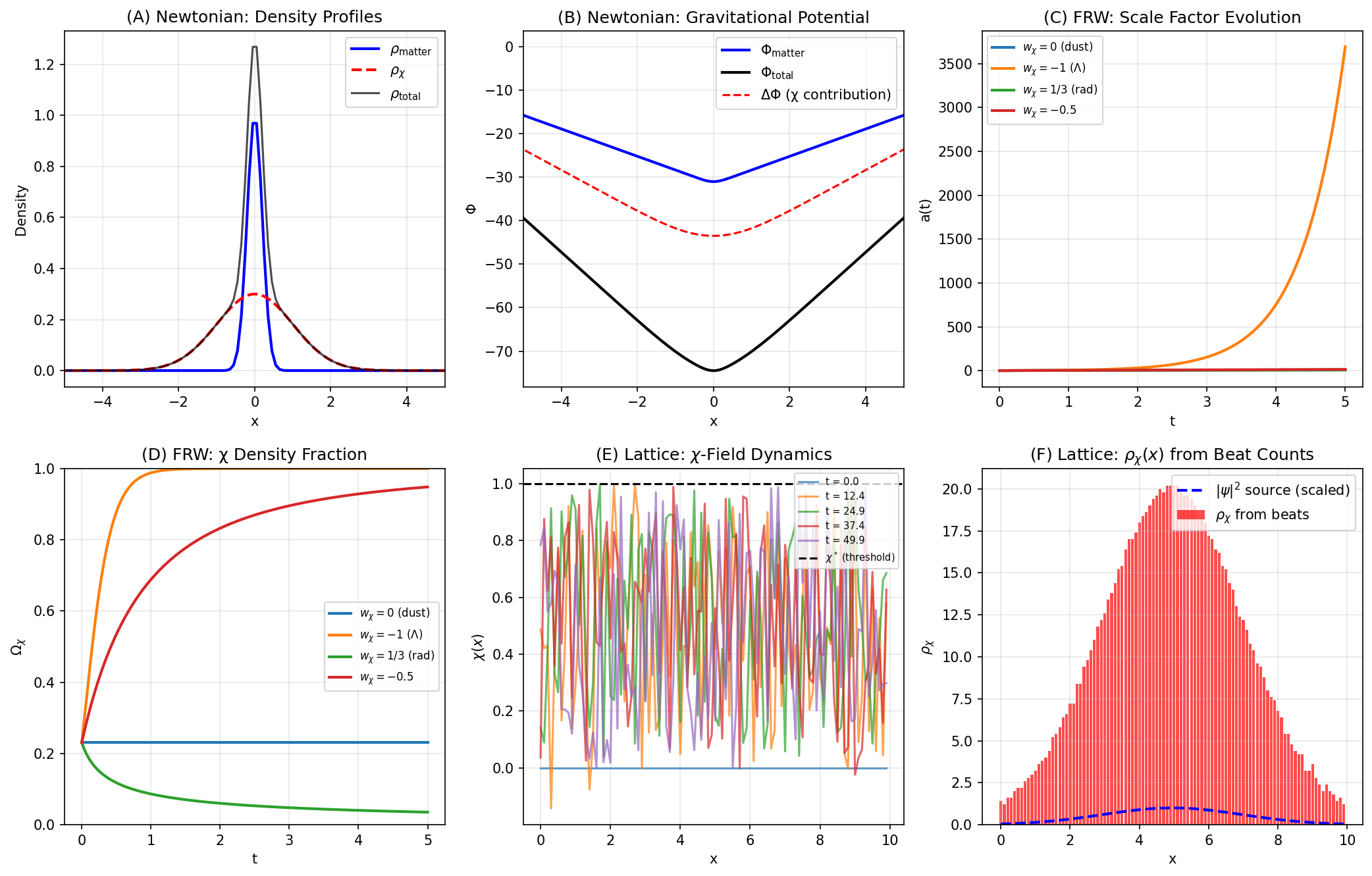
V48 behavioral stress energy: Newtonian, FRW and lattice results

図1：ニュートン重力ポテンシャル、FRW スケール因子 a(t)、χ 密度分率 Ω_χ、さらに格子上での χ フィールドダイナミクスとビート数から再構成した ρ_χ(x) の比較。 χ フィールドが、局所的にも宇宙論スケールでも一貫した重力源としてふるまうことが示されている。

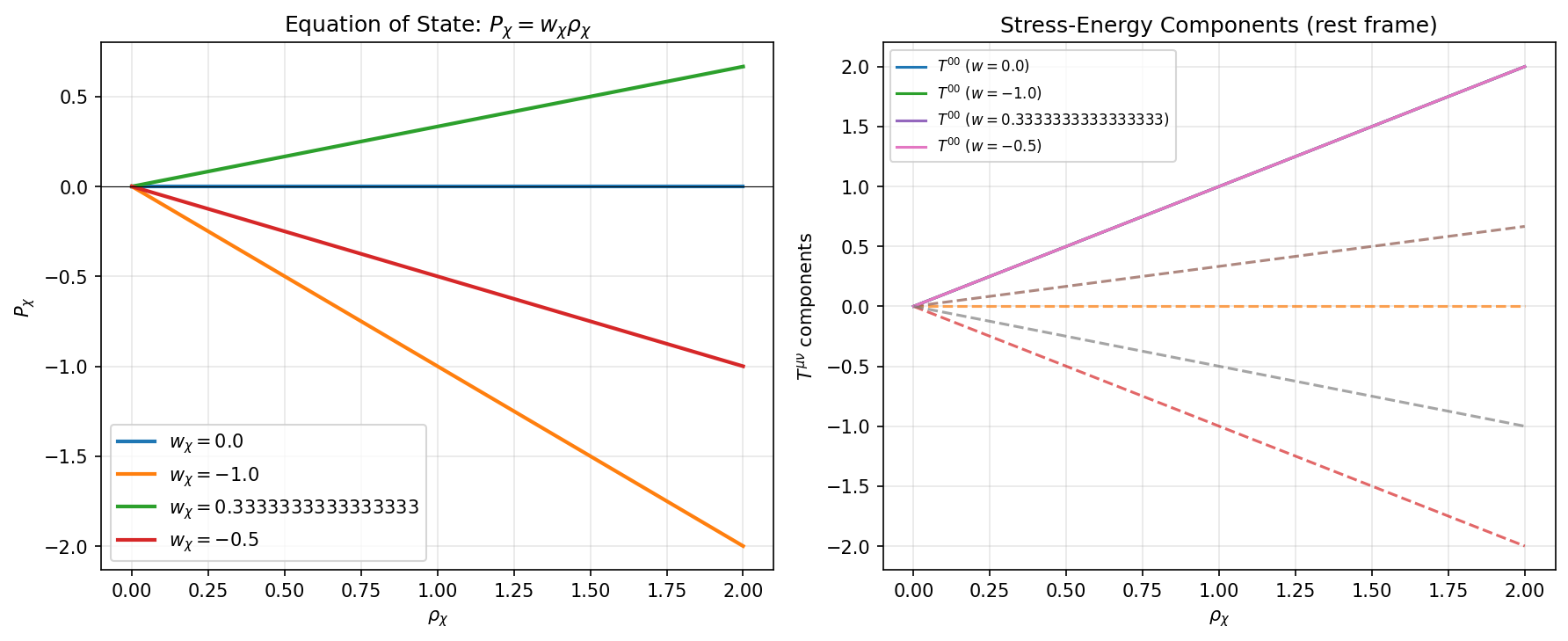
V48 chi-field equation of state and stress-energy components

図2：左：状態方程式 P_χ = w_χρ_χ の直線群。右：静止系における応力エネルギーテンソル成分 T^(χ)_μν の ρ_χ 依存性。実線がエネルギー密度成分 T⁰⁰、破線が空間成分 Tⁱⁱ（i=1,2,3）。

読み進めるためのメモ

このページは英語版 V48 の 公式な翻訳 ではなく、内容の流れと物理的意味を日本語で掴むための解説サイトです。数式の厳密な定義やパラメータ、数値実験の条件などは、必ず Zenodo に登録されたオリジナル PDF と LaTeX ソースを参照してください。

V48 は V35（情報としての重力）、V38（Information Carnot）、V39–V41（χ-フィールド重力）、そして V47（行動的ヒルベルト空間）と強く結びついています。これらの文脈に慣れているほど、w_χ や T^(χ)_μν の物理的意味がクリアになります。

行動的応力エネルギーとしての χ フィールド— wχ と T(χ)μν の構成