χ呼吸のための行動的ヒルベルト空間
— ビート数からコヒーレント状態へ
V41〜V46で構築してきた「χの鼓動(quantum heartbeat)」モデルを、ヒルベルト空間の枠組みに持ち上げた英語論文 V47 の日本語サイトです。
この論文では、各空間セル n に対してビート数 Nχ,n を数えるだけだった V41–V46 の記述を拡張し、 ビート数そのもの をスペクトルにもつ数演算子 N̂χ,n を備えたヒルベルト空間 Hn を導入します。 そのうえで、コヒーレント状態 |α⟩ を用いることで、古典的な χ-鼓動の統計がどのように量子論的に表現できるかを示します。
概要(Abstract)
V41〜V46 では、コミットメント場 χ の時間発展を一次の微分方程式(オーバーダンプドな「心拍」)として記述し、 しきい値 χ* を下から超えるたびに 1 ビートとしてカウントすることで、測定確率 P(x) ∝ |ψ(x)|2(ボルン則)を再現してきました。
V47 では、この古典的なビート数 Nχ,n を、局所的な行動的ヒルベルト空間 Hn ≃ ℓ2(ℕ0) 上の数演算子 N̂χ,n の固有値として扱います。 標準的な生成・消滅演算子 ân, ân† を導入し、χ-コヒーレント状態 |α⟩n を構成することで、 大きな |α| の極限では V41–V46 の古典統計と一致することを示します。
二重スリット干渉、位相緩和による可視度の減衰、ビート数保存の条件などをすべてこのヒルベルト空間上で書き直すことで、 「重力はすでに χ の鼓動レベルで量子化されている」という YAGC 的主張を明確化します。
1. 行動的ヒルベルト空間 Hn
1.1 ローカル空間の定義
空間(より正確には χ フィールドの有意なサポート領域)を、セル n の集合に粗視化します。
各セルに対して、ビート数の列 |N⟩n (N = 0,1,2,...) を基底にもつヒルベルト空間
Hn ≃ ℓ²(ℕ₀) を導入します。
数演算子は
N̂χ,n|N⟩n = N |N⟩n
で定義され、行列としては対角成分 (0,1,2,...) を並べた形になります。
1.2 生成・消滅演算子とビート数
標準的な調和振動子と同様に、ラダー演算子 ân, ân† を
ân|N⟩n = √N |N-1⟩n、
ân†|N⟩n = √(N+1) |N+1⟩n と定義し、
交換関係 [ân, ân†] = I を仮定します。
数演算子は N̂χ,n = ân†ân で与えられます。
ここで重要なのは、これは 場の量子化 ではなく、 V41–V46 で整数値として扱ってきたビート数 Nχ,n を、 そのまま演算子の固有値として読み替える 行動的なアンサッツ であるという点です。
2. χ-コヒーレント状態と古典極限
2.1 χ-コヒーレント状態
任意の複素数 α に対して、χ-コヒーレント状態を
|α⟩ = e-|α|²/2 ΣN=0^∞ αⁿ / √(N!) |N⟩
と定義します。これは通常の光のコヒーレント状態と同じ数学的構造をもち、
â|α⟩ = α|α⟩ を満たします。
このとき、ビート数演算子の期待値と分散は
⟨N̂⟩ = |α|²、
Var(N̂) = |α|² となり、
ポアソン分布に従うことがわかります。
2.2 V41–V46 との対応
V41 の数値実験では、各位置 x ごとに χ(t, x) のしきい値超え回数をカウントし、 長時間平均したビート数 Nχ(x) が |ψ(x)|2 と高い相関(r > 0.999)をもつことが示されました。
V47 では、各セル n の期待ビート数 ⟨N̂χ,n⟩ を |αn|2 と同一視することで、 「大きな |αn| の極限においては、古典的なビート数統計と χ-コヒーレント状態のポアソン統計が一致する」 ことを示します。これにより、行動的モデルとヒルベルト空間モデルを滑らかにつなぐ橋がかかります。
3. 干渉・位相緩和・コヒーレンス長
3.1 二重スリット実験の再表現
V45 では、χ-呼吸のコヒーレンス長 Lcoh(γ, D) を導入し、 ノイズ強度 D や減衰率 γ に応じて干渉縞のコントラストがどのように劣化するかを解析しました。
V47 では、スリット A, B を通る χ-状態を |αA⟩, |αB⟩ として表現し、
スクリーン上の一点に対応する状態を重ね合わせ
|Ψ⟩ = cA|αA⟩ + cB|αB⟩ と書きます。
可視度 V は、これらの χ-状態の重なり ⟨αA|αB⟩ の実部 Re[⟨αA|αB⟩] として表され、
V41 の「ビート分布 vs. |ψ|2」という結果と整合する形で定式化されます。
3.2 位相緩和とコヒーレンス長
環境との相互作用や内部ノイズは、χ-状態に対する位相緩和チャネルとしてモデル化されます。
単純な位相減衰モデルでは、コヒーレント状態の重なりが
⟨αA|αB⟩ → e-ΓL ⟨αA|αB⟩
のように距離 L とともに指数関数的に減衰し、その特性長 1/Γ が
V45 で定義された Lcoh に対応します。
4. 重力の量子化の意味づけ
4.1 「粒子」ではなく「パターン」としての量子化
V46 で提案されたように、本シリーズにおける「重力の量子化」とは、 メトリック gμν を演算子化し新しい粒子(グラビトン)を導入することではありません。 むしろ、 χ フィールドの鼓動が、もともと離散的なビート単位でしか変化しない という行動レベルの事実こそが量子性の源だとみなします。
V47 は、このビートの離散性をヒルベルト空間上の数演算子 N̂χ,n として形式化し、 「重力はすでに χ-呼吸のレベルで量子化されている」という主張を、数学的にも整理しています。
4.2 V48〜V50 への接続
後続の V48 では、ビート数の期待値から χ-エネルギー密度 ρχ を定義し、 有効な応力エネルギーテンソル T(χ)μν を構成して重力場方程式に結びつけます。 V49, V50 では、ブラックホール熱力学や宇宙論的揺らぎへの応用が検討されています。
図:V47 概念図
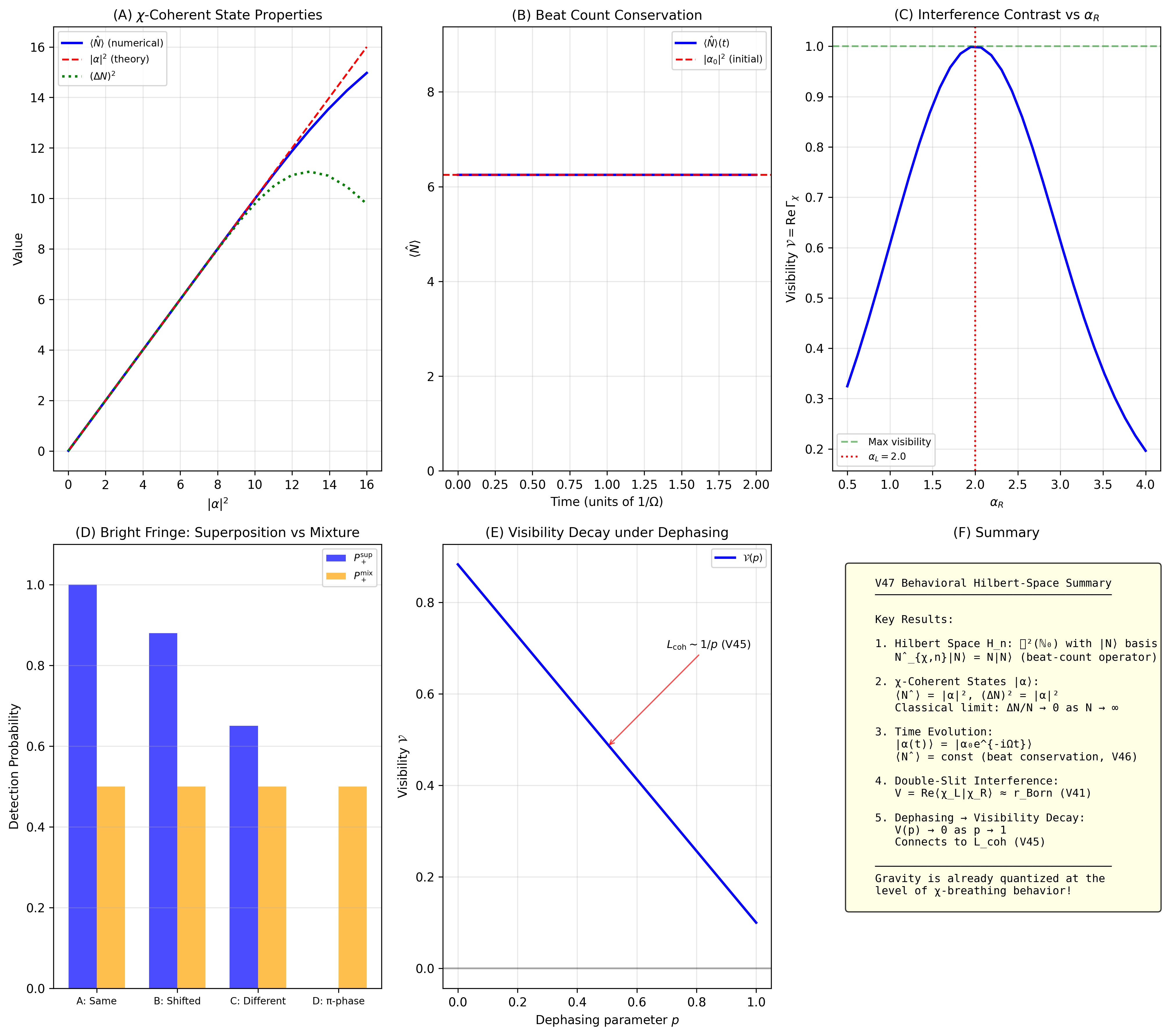
図1:V47 の主要な数値・概念結果のまとめ。 (A) χ-コヒーレント状態の性質、(B) ビート数保存、(C) 交差コントラスト、 (D) 明線の強度分布、(E) デコヒーレンスによる可視度減衰、(F) 論文全体のサマリー。 論文では、これらを通して「行動的ヒルベルト空間」と「χ-重力」の接続が段階的に示されます。
読み進めるためのメモ
このページは英語版 V47 の 公式な翻訳 ではなく、 内容の流れと物理的意味を日本語で掴むための解説サイトです。 数式の厳密な定義や証明、数値実験の詳細については、 必ず Zenodo に登録されたオリジナル PDF を参照してください。
また、V47 は V16, V26, V35, V38〜V46 までの文脈の上に立っています。 「呼吸関数」「Reality Tax」「χ-フィールド重力」「Information Carnot Bound」 といったキーワードになじみがない場合は、先にそれらの巻の解説ページを読むことをおすすめします。