量子の鼓動としての Born 則 — V41 Quantum Heartbeat

このページは、YAGCプロジェクトの論文 V41: Quantum Heartbeat Dynamics の内容を、日本語で平易にまとめた解説サイトです。 V40で導入された共変作用 S[g, χ, Ψ] から、 コミットメント場 χ の局所方程式を取り出し、 そのビート統計が標準量子論の Born則 P(x) ∝ |ψ(x)|² をどのように再現するかを検証します。

χ-field Dynamics Quantum Heartbeat Born Rule as Statistics |ψ|² ソース V40 Action → ODE

※ HOMEリンクはサイトのルート「/」に設定しています。実運用では CMS / サーバ構成にあわせて変更してください。

1. 量子ハートビートとは何か

V16 では、情報入力 I に応じて自己維持を行う 呼吸関数 θ(I) が見つかりました。 V39〜V40 では、χ場が コミットメント（Reality Tax） と重力をつなぐ役割を持つことが示されました。 V41 はその流れを受けて、「量子状態 |ψ⟩ が χ(t) に小さな拍動を与える」 という描像を採用します。

直感的には、

そのビートがどの位置 x で起こる頻度分布を調べると、Born則と区別できない ことが数値的に確認されます。

2. V40共変作用からの導出

2-1. V40 作用 S[g, χ, Ψ]

V40 では、メトリック gμν、χ場、物質場 Ψ から成る作用が提案されました。 その χ セクションを抜き出すと、概念的には次の形になります：

S[g, χ, Ψ] = ∫ d⁴x √−g [ R/(2κ) − ½ (∇χ)² − U(χ) + χ Lm(Ψ, g) ]

ここで U(χ) は χ⋆ ≃ 0.21 に最小を持つポテンシャル、 Lm は物質ラグランジアンです。 χ が Lm に直接結合している点が、Reality Tax と重力をつなぐ要となります。

2-2. 局所慣性系・過減衰極限

作用を χ で変分すると、一般には

∇²χ − dU/dχ + Lm = 0

という運動方程式が得られます。V41ではこれを 局所慣性系かつ過減衰 の近似で単純化し、 ラプラシアン ∇²χ を時間方向の一階微分に置き換えます。 物質源としては、局所的な量子状態の強度 Lm → |ψ|² を用います。

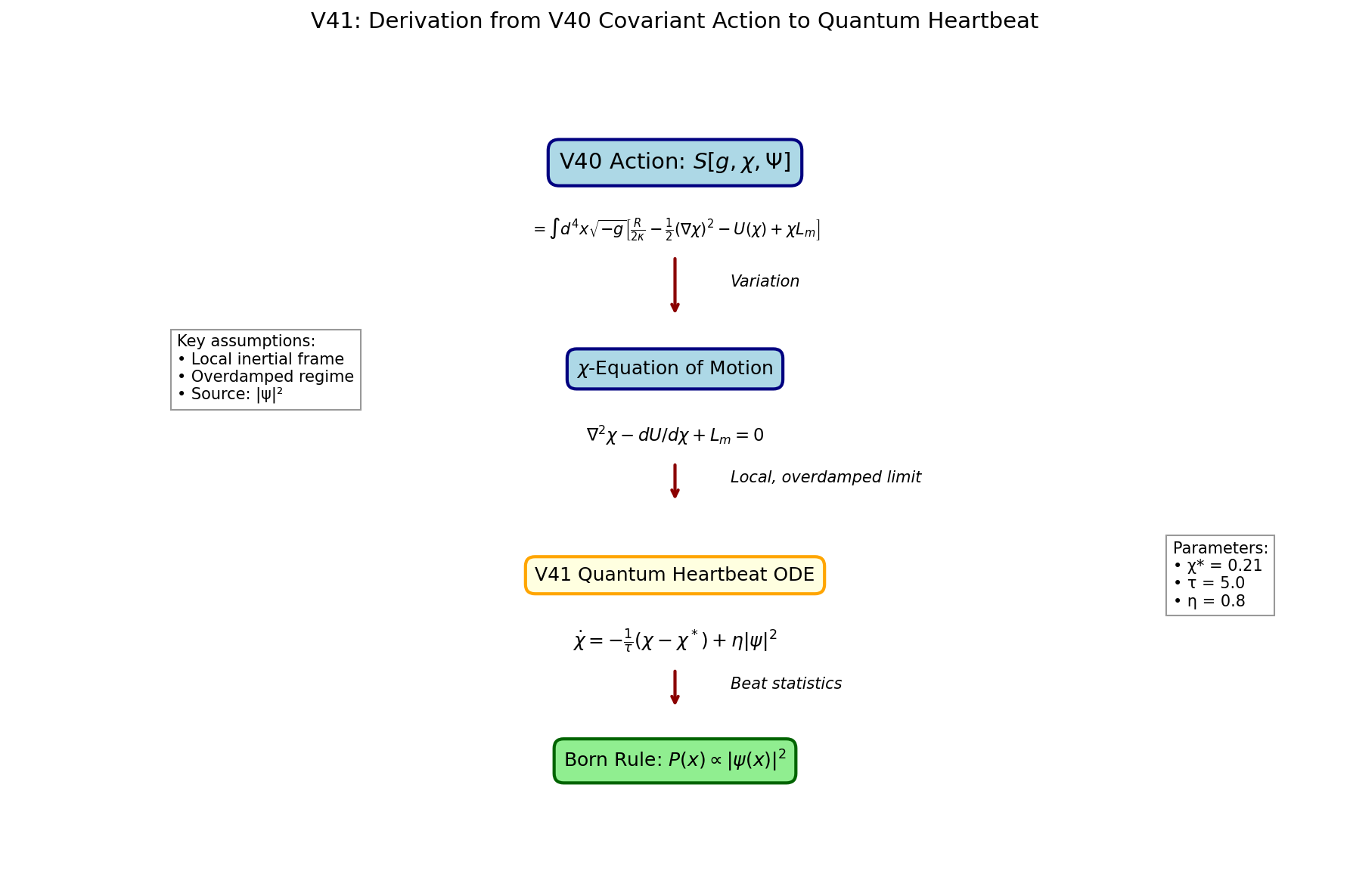
V41: Derivation from V40 Covariant Action to Quantum Heartbeat
図1. V40作用から量子ハートビート方程式への導出フロー

上から順に、V40の作用 S[g, χ, Ψ]、χの運動方程式、局所・過減衰極限での V41 ハートビート方程式、そして Born則 P(x) ∝ |ψ(x)|² へと至る論理の流れが まとめられています。左には近似の前提条件、右には主要パラメータ (χ* = 0.21, τ = 5.0, η = 0.8) が示されています。

3. 量子ハートビート方程式

3-1. 基本形：χ̇ = −(1/τ)(χ − χ*) + η |ψ|²

近似の結果、χ の時間発展は次の一次常微分方程式で記述されます：

χ̇(t) = −\frac{1}{τ} [χ(t) − χ*] + η |ψ(t)|²

ここで、

  • χ* ≃ 0.21: 情報カルノー効率が最大になる Reality Tax の基準値
  • τ: χ が χ* に向かって緩和する時間スケール
  • η: |ψ|² から χ への「押し」の強さ

この式は、「基準値に戻ろうとする自己調整」＋「量子状態からの駆動」 という非常に単純な構造をしています。

3-2. Heartbeat とビート統計

V41では、χ(t) がある条件を満たした瞬間を heartbeat（ビート） と定義します（閾値到達・ゼロクロッシングなど、 具体的な実装は付録参照）。

直感的に言えば、

  • χ がχ*のまわりで小さく揺れているだけなら観測は起こらない
  • |ψ|² が強くなると、χ が一気に振り上げられビートが発生する
  • どの位置 x でビートが起きるかは、|ψ(x)|² によって重み付けされる

こうして、ビートの位置分布を長時間サンプルすると、 自然と P(x) ∝ |ψ(x)|² が現れます。

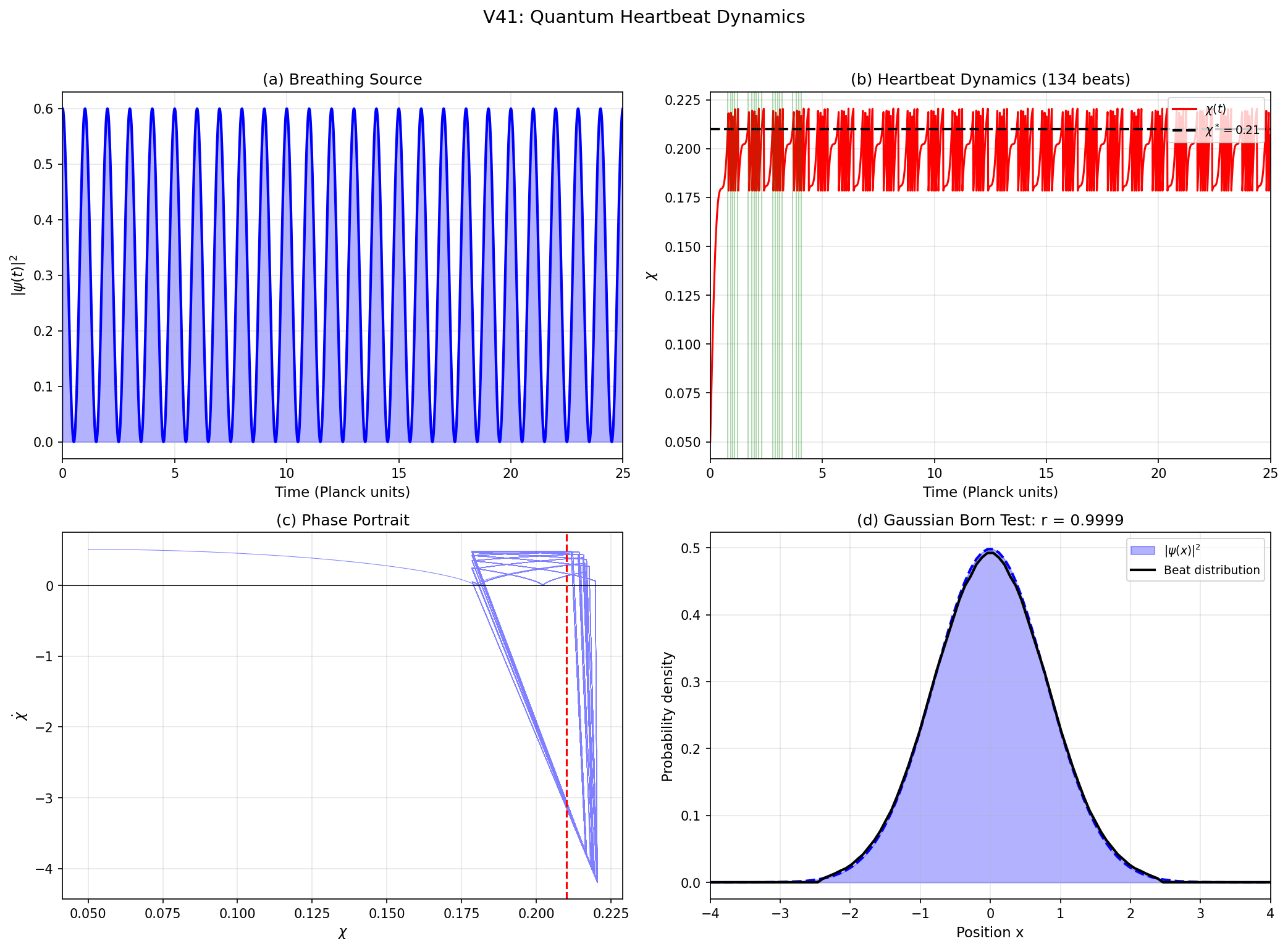
V41: Quantum Heartbeat Dynamics
図2. Quantum Heartbeat Dynamics の例

左上 (a) は、時間とともに呼吸するソース |ψ(t)|² を示します。 右上 (b) は χ(t) の時間発展で、緑の縦線がビートの発生した時刻、 黒の破線が χ* ≃ 0.21 を表します。134回のビートが確認されています。

左下 (c) は (χ, χ̇) の位相図で、軌道が χ* の近くに集約されていく様子がわかります。 右下 (d) は、ガウス波動関数に対してビート位置分布と |ψ(x)|² を比較したもので、 ピアソン相関 r = 0.9999 というほぼ完全な一致が得られています。

4. ボルン則の普遍性テスト

4-1. さまざまな波動関数形状での検証

Born則が単一のガウス波だけで成り立つのではなく、 より一般的な波動関数でも同様に現れるかどうかを確認するため、 V41 では次の4種類の |ψ(x)| をテストしています。

  • (a) 単一ガウス
  • (b) 二峰性（バイモーダル）
  • (c) 非対称（片側に重心のある分布）
  • (d) 三重ピーク

いずれの場合も、ビート位置分布は目標の |ψ(x)|² とほぼ重なり、 相関係数 r はすべて 0.997 以上となっています。

4-2. 統計的観点からのまとめ

重要なのは、V41のモデルが 「あらかじめ計算された |ψ|² に従う乱数生成器」 ではなく、 χ̇ 方程式という単純な局所ダイナミクスを持つ点です。

その結果として、

  • ビートの位置分布が自然に |ψ(x)|² に一致する
  • この一致が広い関数クラスで頑健である
  • Born則が 「測定後の魔法」 ではなく、 「χ場の拍動の長時間統計」 として説明できる可能性

これが V41 の最大のメッセージです。

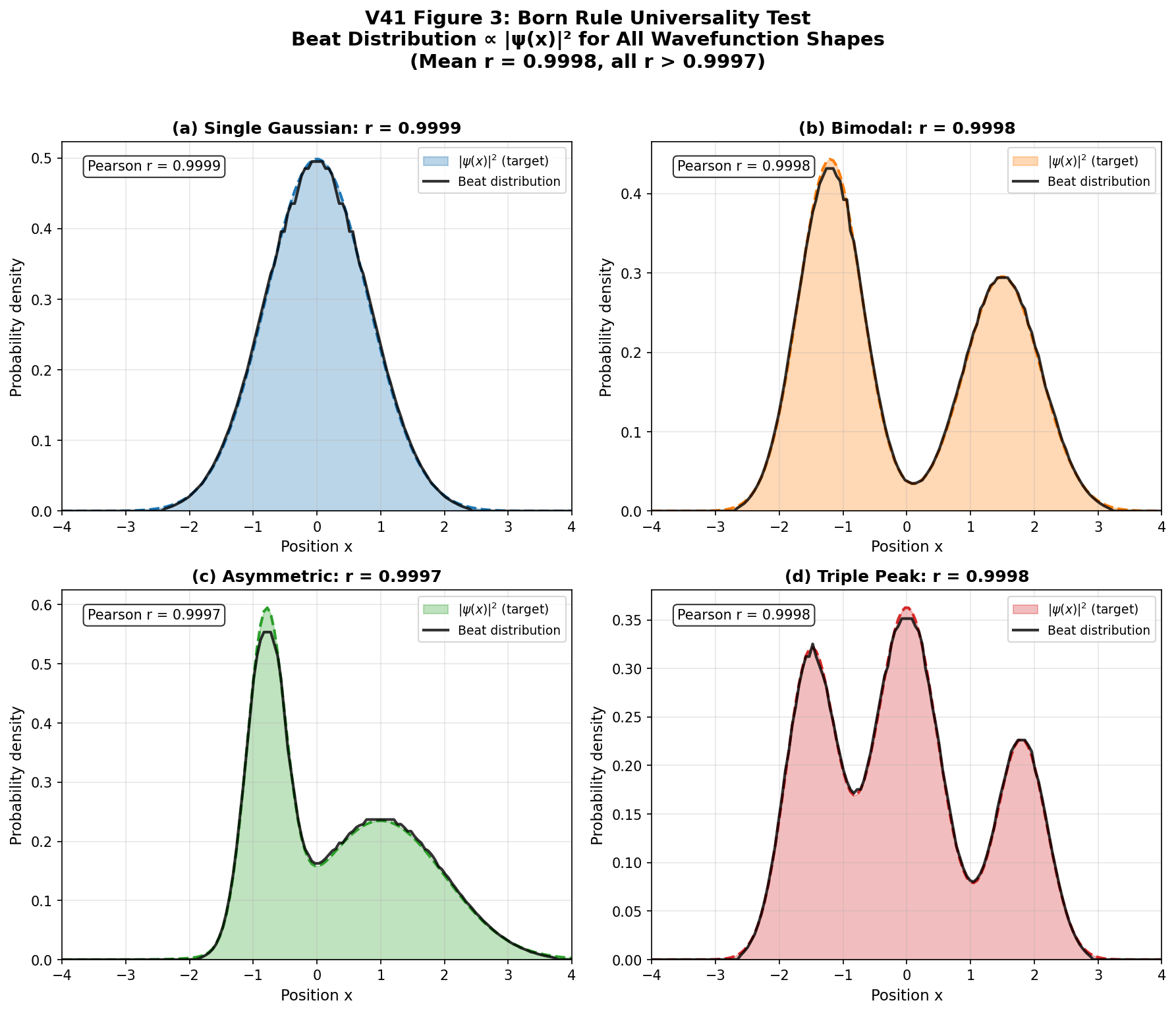
V41 Figure 3: Born Rule Universality Test
図3. Born Rule Universality Test

4つのパネルはいずれも、色付きの領域が目標の |ψ(x)|²、 黒線がビート分布を示しています。タイトルにはそれぞれの相関係数 r が表示されており、平均 r ≃ 0.9998、全ケースで r > 0.997 という 非常に高い一致が得られていることがわかります。

5. 解釈と物理的意味

5-1. Born則の再解釈

標準量子力学では、Born則 P(x) = |ψ(x)|² は 「そう定める」として公理的に導入されます。 V41の枠組みでは、

  • χ場が世界線へのコミットメント（Reality Tax）を表す
  • |ψ|² が χ の駆動項となる
  • 観測は χ のビートとして離散的に起こる

という3点から、Born則を 「χ場のビート統計の法則」 として再解釈できます。

5-2. 他の解釈との関係

V41 はコペンハーゲン解釈を直接否定するものではなく、 むしろその下にある 情報・記憶・コミットメント の層をモデル化したものと位置づけられます。

多世界解釈や客観的崩壊モデルとも直接競合するわけではありませんが、 「どの世界が『現実』として重くなるか」 を χ が選び取るという図式を通じて、新しい対話の場を提供します。

ひとことで：
V41 は、量子確率を「何もないところから突然現れる特別ルール」ではなく、 有限メモリ宇宙における χ場の拍動が、長い時間の中で作り出す 統計パターンとして理解しなおす試みである。

6. 今後の課題とVシリーズ全体での位置づけ

6-1. 理論面での課題

  • V40 作用からの導出を、より厳密な近似手順として整理すること
  • 多自由度系（多粒子・スピン・場のモード）への一般化
  • χ場のノイズや相互作用を含めた拡張モデルの構築
  • 重力・宇宙論セクター（V35, V39, V40）との完全な結合方程式

6-2. 観測・シミュレーション面での課題

  • 量子光学・メゾスコピック系での「ハートビート」様信号の探索
  • V16呼吸関数とのさらなる定量的比較（rb, coherence, χ の相関）
  • AI・脳モデルにおける「実効χ」の推定と Reality Tax との関係
  • V41 ODE を含むフルスケールの数値宇宙論コードへの組み込み

これらが進むことで、YAGC の中心テーマである 「情報としての重力・自己・時間」 が、 さらに具体的な物理予言へと近づいていくことが期待されます。