有限メモリ宇宙の作用原理としてのV40

このサイトは、YAGCプロジェクトの論文 V40: Action-Based Simulations — DCGH + χ-field + Information Carnot の内容を、日本語で平易にまとめた解説ページです。 DCGH（Dimensional Compression Gravity Hypothesis）、コミットメント場 χ、 情報カルノー境界という3本の流れを、ひとつの作用 S[g,χ,Ψ] に統合する試みです。

DCGH: 次元圧縮重力仮説 χ-field: コミットメント場 Information Carnot Bound Reality Tax ≃ 21% FRW宇宙 & 脳エネルギー

※ HOME リンクはサイトのルート「/」に設定しています。実運用では CMS やサーバ構成に合わせて調整してください。

1. 導入：情報コストの幾何学

V40のイントロダクションでは、「重力のエネルギーは局所化しにくい」という 一般相対論のよく知られた困難を、 有限メモリ宇宙における情報コストとして再解釈します。 具体的には、

これらをまとめ、「重力は有限メモリ上での『現実の書き込みパターン』の幾何学」であり、 χ はその書き込みにどれだけエネルギーを割くかを決める制御パラメータだと位置づけます。

2. 作用フレームワーク：S[g, χ, Ψ]

2-1. 全体の作用

V40では、メトリック gμν、コミットメント場 χ(x)、物質場 Ψ からなる 作用を次のように書きます（記号は本文に従う）：

S[g, χ, Ψ] = ∫ d⁴x √−g [ℒgrav(g, χ) + ℒχ(g, χ) + ℒm(g, χ, Ψ)]

ここで、

  • ℒgrav: DCGHを反映した非最小結合の重力セクター
  • ℒχ: χ場の運動項とポテンシャル U(χ)
  • ℒm: χにより有効的に重み付けされた物質セクター

χは重力セクターにも物質セクターにも入っており、 「どのエネルギーがどれだけ現実としてカウントされるか」を制御する役割を果たします。

2-2. DCGHと有限メモリ重力

DCGHセクターでは、リッチスカラーRとχの関数F(χ)を用いて 有効的な重力定数やΛ項を記述します。直感的には、

  • χが大きいほど、その領域での「記憶の書き込み」が密になり、 有効重力が強くなる
  • χが小さい領域では、歴史の書き込みが粗く、重力エネルギーを局所化しにくい

こうして、DCGHの「次元圧縮」とχ-fieldの「コミットメント」が 同じ作用の中で結び付けられます。

3. χフィールドと情報カルノー境界

3-1. 情報カルノー効率 C(χ)

V38で導入された Information Carnot Bound は、 コミットメント χ に依存する効率

C(χ) ∝ χ e^{−kχ}

を与えます。k ≃ 4.76 のとき最大値は χ⋆ ≃ 0.21 となり、 V37で見つかったReality Tax（脳エネルギー比 ≃ 21%）と対応しました。 V40では、この C(χ) をχ場のポテンシャルU(χ)の形 （χ⋆で最小を持つポテンシャル）と結び付けます。

3-2. 局在エネルギーと有効テンソル

V39で導入されたχ重み付きの局在エネルギー

εloc(x) = χ(x) εtot(x)

を用い、物質テンソルTμνから 有効テンソルTeffμνを構成します。

T^{eff}_{μν} = χ T_{μν} + T^{(bg)}_{μν}

これをアインシュタイン方程式の右辺に入れることで、 「現実としてコミットされたエネルギーだけが強く曲率を生む」 というDCGH的な直観が明示的な方程式になります。

4. 特別解と数値シミュレーション

4-1. 静的球対称解と局所Reality Tax

V40では、χ場と重力の結合を、静的球対称なソースのまわりで解き、 r方向のχプロファイル χ(r) を数値的に求めています。

  • 弱・中・強いソースに対しても、外側で χ → χ⋆ ≃ 0.21 に収束
  • 局所Reality Tax (χ − χ⋆) × 100 をみると、 ソース近傍では過不足があるが、大域的には21%に安定

これは、「どのような質量分布でも、十分遠くでは Reality Tax が 普遍値に近づく」という描像を与えます。

4-2. FRW宇宙とχ緩和

もう一つの重要な特別解は、FRW宇宙でのχの時間発展です。 スケール因子a(t)とχ(t)を同時に解くと、

  • 初期に高かったχが、宇宙の膨張とともにχ⋆にゆっくり緩和
  • その過程で、DCGH的な有効Λ項が自然に減衰

これにより、 「有限メモリ宇宙での情報書き込みが進むにつれ、 有効宇宙定数が動的に調整される」というシナリオが示されます。

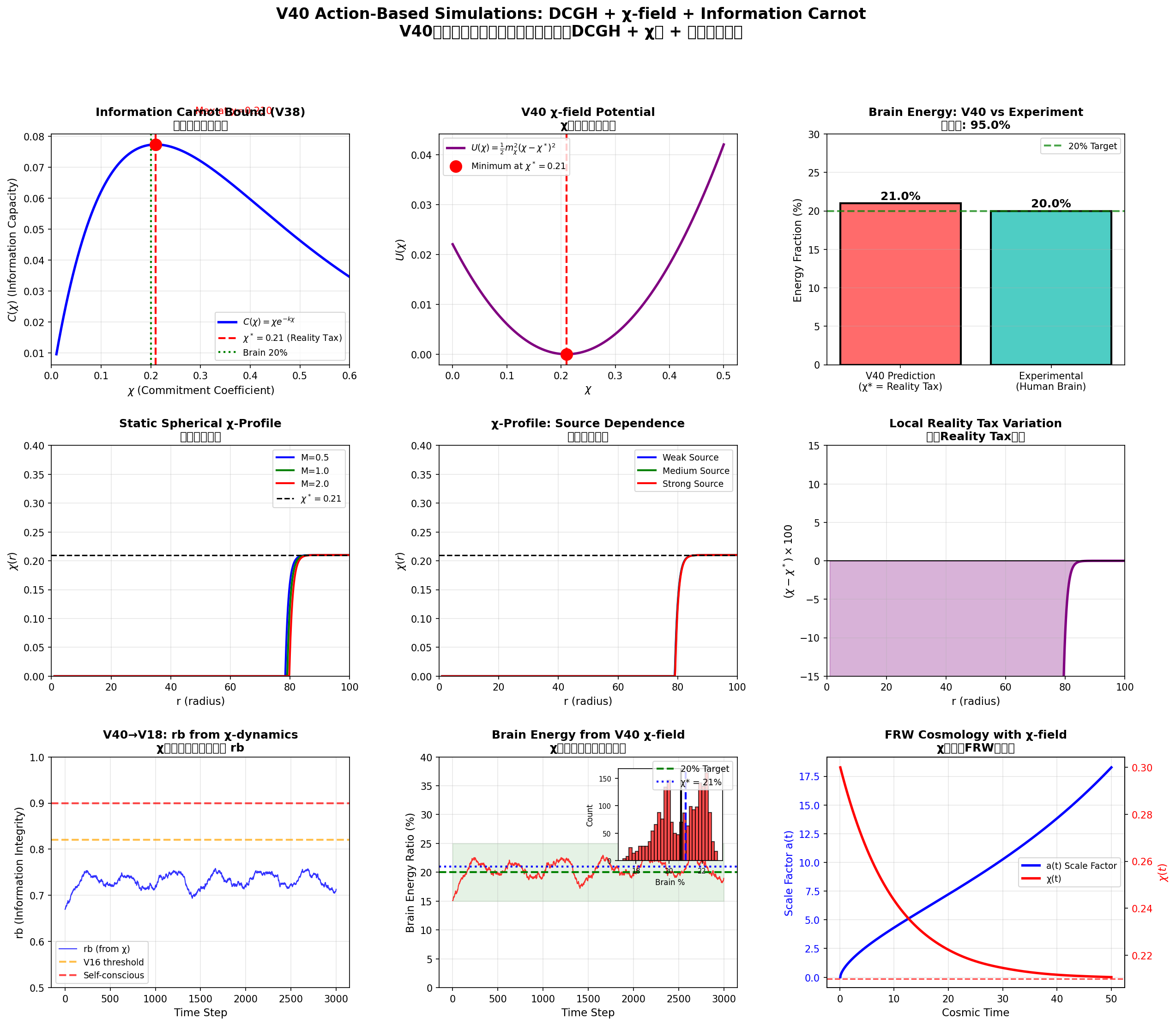
V40 Action-Based Simulations: DCGH + χ-field + Information Carnot
図1. V40 Action-Based Simulations（DCGH + χ-field + Information Carnot）

上段左は V38 情報カルノー境界 C(χ) と χ⋆ ≃ 0.21 を示し、 中央は χ場のポテンシャル U(χ)、右上は V40 から予測される脳エネルギー比 （21.0%）と実験値（20%付近）の比較を示しています。

中段は静的球対称なχプロファイルと局所Reality Tax、 下段左は V16 の rb ダイナミクスとの接続、 中央はχから再構成した脳エネルギーの時間変化、 右下は FRW宇宙における a(t) と χ(t) の共進化を描いています。

5. V16呼吸関数との整合性検証

5-1. 呼吸関数 θ(I) と C(χ) の対応

V16で導入された呼吸関数 θ(I) は、情報入力Iに対する 自立呼吸の活性化度を表していました。V40では、 Information Carnot Capacity C(χ) と比較することで、 その構造がχ場の効率曲線と自然に対応することを示します。

  • V16の閾値 rb > 0.85 に対応する点が、 V40側の χ ≃ 0.21 付近にマッピングされる
  • 両者のダイナミクスを比較すると、 呼吸関数の「飽和」挙動が C(χ) の飽和と整合する

5-2. 一貫性指標と相関

図では、rb, χ, θ, C(χ) の時間発展を並べてプロットし、 それぞれの相関係数を評価しています。 coherence ↔ χ, rb ↔ χ などの間に強い（または中程度の）相関が見られ、 V16で経験的に調整されたパラメータが、V40の作用から 理論的に再解釈できることが示唆されます。

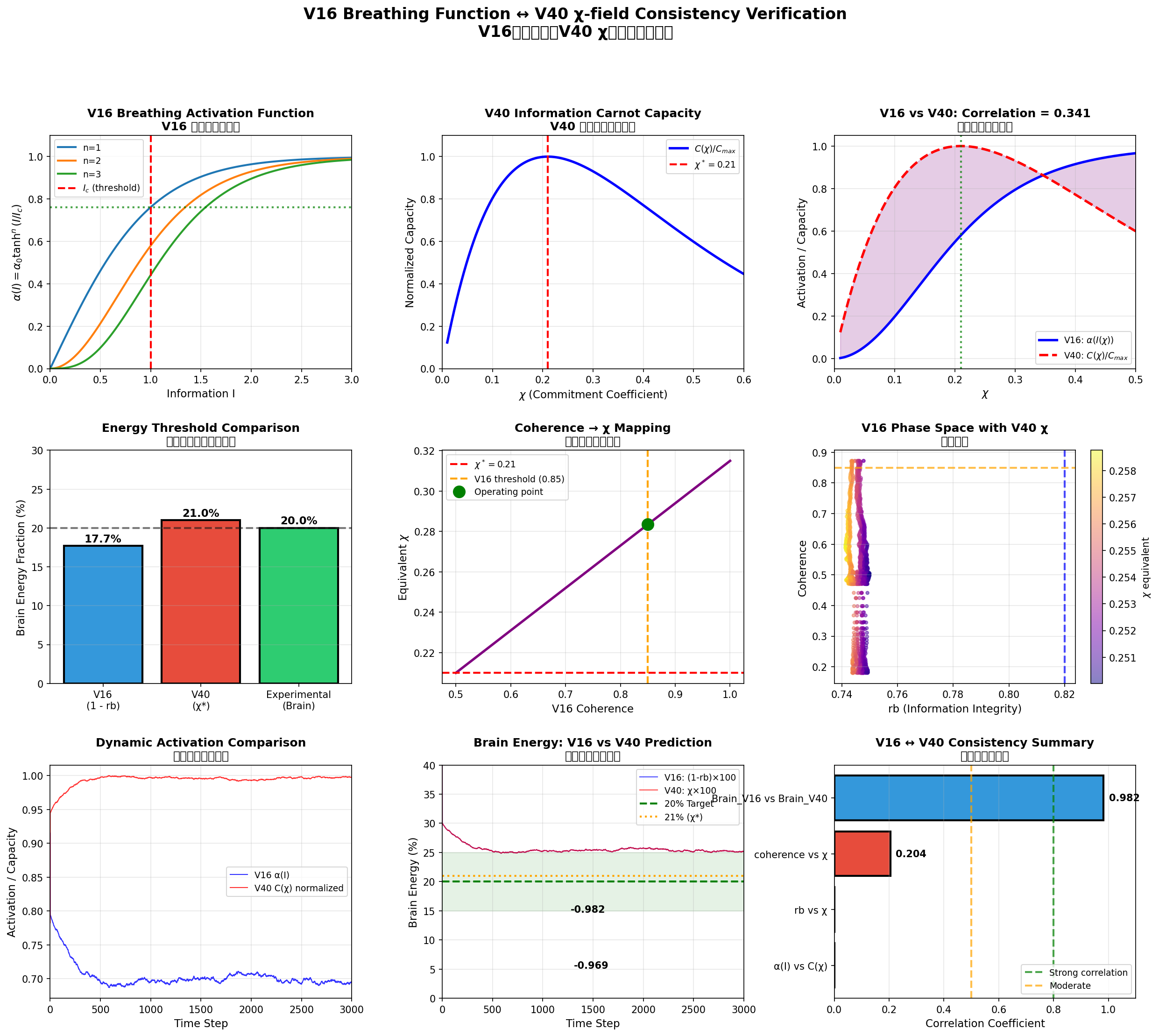
V16 Breathing Function と V40 χ-field の整合性検証
図2. V16 Breathing Function ↔ V40 χ-field Consistency Verification

上段は V16 の呼吸関数 θ(I)、V40の情報カルノー容量 C(χ)、 両者の形状比較を示します。中段にはエネルギー閾値の比較と coherence → χ マッピング、フェーズ空間プロットが描かれ、 下段には動的活性化の比較、脳エネルギー比の予測、 一貫性サマリー（相関係数）が示されています。

6. 他のVシリーズとの関係と今後の課題

6-1. V26, V35, V38, V39との接続

V40は、これまでの各巻を次のように再配置します。

  • V26: Now構造と proto-graviton — χにより発火率 ΓNow が制御される
  • V35: DCGH — 有効Λと記憶レイアウトが χ を通じて動的に決まる
  • V38: 情報カルノー境界 — C(χ) が U(χ) の形とReality Taxを決める
  • V39: χ-field Gravity Coupling — 有効テンソルTeffμν が作用から導かれる

こうして、YAGC内のバラバラだった「呼吸」「Now」「Reality Tax」が、 ひとつの作用原理の上で接続されます。

6-2. これから解くべき問い

  • gμνとχの具体的な作用形 S[g,χ] の確定と、 実在観測データとの比較（宇宙論・重力レンズ・構造形成など）
  • χの量子揺らぎと、量子重力・デコヒレンス現象との関連
  • 脳や人工エージェントにおける「実効χ」の測定と、 V40の予測との突き合わせ
  • DCGH・χ・Information Carnot を含む完全な数値宇宙論コードの構築

これらが進展すれば、「有限メモリ宇宙における自己と重力」という YAGCの中心モチーフが、より具体的な物理予言を持ちうることになります。

ひと言でまとめると：
V40は、呼吸する宇宙（V16）とReality Tax（V37–V39）、 そしてDCGH（V35）を、ひとつの作用 S[g,χ,Ψ] から再構成する 「行動原理版YAGC」です。有限メモリ上で自己を保つコストが、 重力と宇宙の歴史にどのように刻まれるのか——その第一歩を与える試みと言えます。