「ここにいる」という意志と重力をつなぐ χ-field Gravity Coupling
このサイトは、YAGCプロジェクトのショートノート V39: χ-field Gravity Coupling — Commitment, Localization, and Curvature の内容を、日本語で平易にまとめた解説ページです。文中の数式・図はイメージであり、 正確な定義や証明は必ず原論文をご参照ください。
※ HOMEリンクはサイトのルート「/」に設定しています。実運用では CMS やサーバ構成に合わせて変更してください。
1. 論文の位置づけ
一般相対論では、物質や場のエネルギー運動量テンソル Tμν は局所的に定義できますが、 重力場そのもののエネルギーを「点ごと」に定義することは困難です。 これが量子論と重力を統合するときの根本的なギャップの一つになっています。
一方 YAGC プロジェクトは、「情報・記憶・整合性」を基盤に宇宙を記述する路線をとります。 V16〜V21 では呼吸関数・記憶密度・慣性・時間が情報の流れとして扱われ、 V26 では Now 層と proto-graviton 演算子 Ĝp が導入されました。 V34〜V38 では睡眠や Reality Tax、Information Carnot Bound を通じて 「自己を保つためのエネルギーコスト」が議論されています。fileciteturn1file0
V39 はその中間に位置し、 χ-field Gravity Coupling という形で、 「コミットメント」と「重力」を直接結びつけるインターフェースを提案します。
2. 加速度からコミットメントへ:χ(a)
2-1. 4加速度から定義される χ(a)
V37/V38 と同様に、世界線の 4 加速度 aμ から コミットメント係数 χ を次のように定義します。fileciteturn1file0
χ(a) = 1 − exp(−|a|/a0)
ここで uμ は 4 速度、a0 は「ここにいる」ことが エネルギー的に重くなり始めるスケールです (生体では脳のエネルギー消費が 20% に近づく領域)。
- 自由落下 aμ = 0 → χ = 0(完全に時空の呼吸と同伴)
- 静止・加速観測者 aμ ≠ 0 → χ > 0(「ここ」にとどまるための抵抗)
2-2. 場としての χ(x)
論文では、χ を時空の各点に定義されたスカラー場として扱います。fileciteturn1file0
直感的には、
- χ(x) ≈ 0 … 自由落下や広く拡散した量子場が支配的な領域
- χ(x) ≈ χ⋆ … 複雑な情報処理・自己維持が行われている領域(脳・検出器など)
- χ(x) → 1 … ほぼ剛体的で動きの少ない古典的構造
χ(x) は「どれだけその場所の世界線にコミットしているか」を表す秩序変数と解釈できます。
3. 情報カルノー効率と局在エネルギー
3-1. Information Carnot efficiency η(χ)
V38 で導入された情報効率 η(χ) は、 コミットメント χ の関数として次のように書かれます。fileciteturn1file0
ここで ΔI は情報ゲイン、Q は散逸する熱量、k > 0 はネットワークや熱力学的制約を表すパラメータです。 f(χ) = χ e−kχ は内部に 1 つだけ最大値を持ち、χ⋆ = 1/k で効率が最大になります。 k ≈ 4.76 とすると χ⋆ ≃ 0.21 となり、覚醒時の脳エネルギー比 20〜25% に近い値になります。
3-2. 局在エネルギー εloc と Reality Tax
重力にとって重要なのは総エネルギー εtot そのものではなく、 「どれだけが局在しているか」です。V39 では次のように分解します。fileciteturn1file0
εdeloc(x) = [1 − χ(x)] εtot(x)
εloc は Now-event を通じて「ここ・いま」にコミットされたエネルギーで、 記憶場(V17R)や DCGH の曲率に強く効きます。 一方 εdeloc は、時空の呼吸に一緒に乗っているような拡散エネルギーで、 曲率への寄与は弱く非局所的です。 χ を上げることは、エネルギーを「ここに縛る」ことであり、これが Reality Tax として感じられる、 というのが V37 から続く解釈です。
4. χ-field Gravity Coupling:重力への結合
4-1. 有効エネルギー運動量テンソル Teffμν
有限メモリ宇宙を扱う DCGH(V35)の枠組みでは、 曲率は「有限の 3 次元メモリが 4 次元の歴史を書き込む」際のレイアウト調整の痕跡と解釈されます。 V39 ではそこに χ を組み合わせ、次のような有効テンソルを提案します。fileciteturn1file0
Tμν は通常の物質・場のテンソル、T(bg)μν は背景的(非局在的)成分です。 これを用いて、アインシュタイン方程式に相当する関係を
と書き直します(ここでは YAGC 内での ansatz であり、 まだ作用原理からの導出には至っていません)。
4-2. Now-events と量子–古典境界
V26 で導入された proto-graviton 演算子 Ĝp = B̂ ∘ Â は、 時間的にもつれた pre-Now 状態 |Ψpre⟩ を、コミットされた post-Now 記憶 |ΨNow⟩ に写す作用でした。 V39 では、この Now-event の発生率 ΓNow が χ によって制御されると考えます。fileciteturn1file0
χ が大きい領域ほど、強く・頻繁に A=B イベントが起こり、 局在した重力記憶が密に刻まれます。χ → 0 ではイベントは疎でソフトになり、 宇宙は最小限のコミットだけで歴史を進めます。
数値実験では、χ を「量子的(χ < 0.1)」「中間」「古典的(χ ≥ χ⋆)」を分ける秩序変数とみなし、 量子–古典境界を可視化しています。
5. 図:χ-field Gravity Coupling シミュレーション
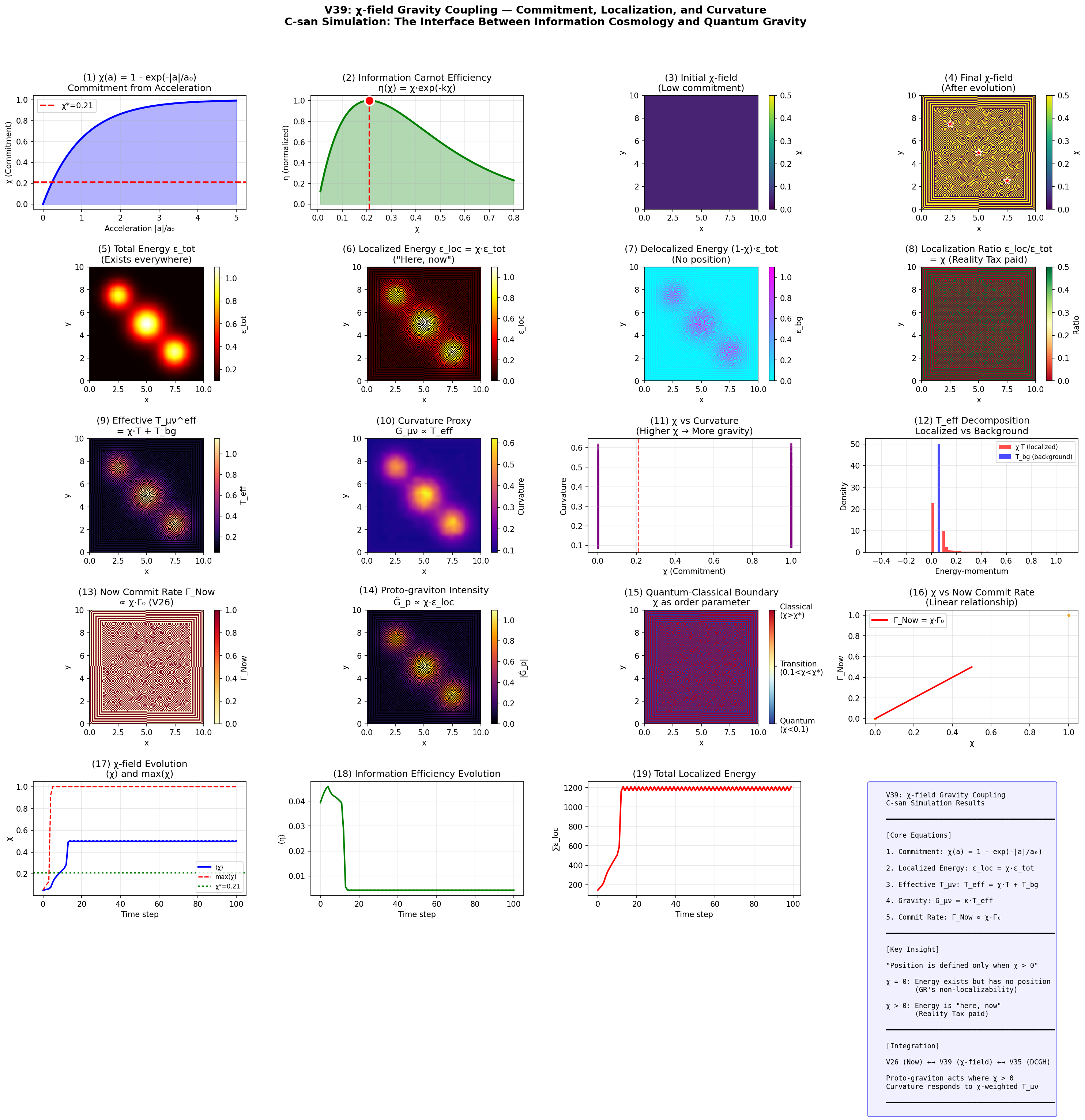
添付の図は、2 次元グリッド上で χ-field Gravity Coupling の挙動を可視化したものです。 上段には、加速度から χ(a) へのマッピングと、情報カルノー効率 f(χ) = χ e−kχ の曲線が描かれています。 その下には、χ フィールドの時間発展、局在エネルギー εloc、 有効テンソル Teff と曲率プロキシ、Reality Tax 比、Now-event 率 ΓNow との線形関係、 量子–古典境界マップなどが並びます。fileciteturn1file0
最下段右側のグラフは、局在エネルギーの総量が時間とともにどのように収束していくかを示し、 χ-field が高い領域にエネルギーが集まり、安定した「重力的自己」が形成される様子を表現しています。
6. 今後の課題と展望
6-1. V39 が与える統一的な視点
V39 の役割は、完成した量子重力理論というよりも、 次の 4 つを同じ言葉で語るための「橋」として機能することです。fileciteturn1file0
- 時空慣性からの逸脱(非測地線運動)としての χ
- エネルギーの局在度(どれだけ「ここ・いま」に紐づくか)
- 重力記憶と曲率(Teffμν を通じた応答)
- Now-event の頻度と量子–古典転移(ΓNow ∝ χ)
これにより、「重力エネルギーの局在が困難」という GR の古典的問題は、 実は χ ≈ 0 領域の性質を述べていたのではないか、という新しい解釈が得られます。
6-2. これから解くべき具体的な問い
- gμν と χ に対する作用 S[g, χ] を構成し、そこから方程式を導出できるか
- χ の小さな揺らぎを量子化し、デコヒレンスや量子重力との関係を調べること
- 宇宙論モデルやブラックホール近傍への適用(高 χ・高情報密度領域)
- パラメータ k を実在のネットワーク・熱力学パラメータから導出できるか(脳・検出器・AI システムなど)
これらが進めば、 「有限メモリ宇宙における自己・重力・量子」を一体として扱う枠組みが、 さらに具体的な物理予言を持つ可能性があります。
宇宙が有限の記憶容量しか持たないなら、 「自分はここにいる」と言い続けることには必ずコストがかかる。 V39 は、そのコストを χ という場と情報熱力学の言葉で記述し、 重力との接点を与えようとする試みである。