V56: 有限情報量子重力理論 (FIQG)

概要 (Abstract)

本論文では、重力と宇宙膨張を有限情報容量に由来する丸め誤差の累積効果として解釈する 有限情報量子重力理論（FIQG: Finite-Information Quantum Gravity）の現象論的枠組みを提案する。

YAGC（Yoshida-AI-Generated Cosmology）の先行研究（V26, V35, V40, V52R, V55）で発展させてきたエネルギー記録描像に基づき、宇宙を離散的な「χビート」によって更新される有限容量の情報媒体としてモデル化する。各更新ステップで不可避的な量子トレランス ε が導入され、これらの局所誤差は消失せずスケールを超えて累積する。

数値実験（SM-1〜3, SM-2b）により以下を示す： (i) 累積誤差は有限情報χ宇宙において √t でスケールする、 (ii) 銀河スケールでは、単一の結合パラメータ α による同一の誤差累積則で渦巻き銀河のフラット回転曲線と楕円銀河のフラット速度分散プロファイルの両方をダークマター的効果として再現できる、 (iii) 宇宙論スケールでは、累積誤差が有効宇宙定数 Λ_eff として作用し、加速膨張を静的宇宙よりも自然な帰結とする。

1. 導入：完璧な宇宙は進化しない

1.1 無限精度の問題

もし宇宙が無限の数値精度を持つ理想的な機械上で計算されていたとしたら、私たちが観測する多くの現象は神秘的なものになるだろう。無限精度の世界では、物理量は完全に正確に表現され、保存則は点ごとに満たされ、すべての進化ステップは丸めや損失なしに実行される。本質的なゆらぎも、構造的不安定性も、そして——議論の余地はあるが——真の時間も存在しない。

私たちの住む宇宙はその正反対である。銀河は回転し構造を発達させ、時空は膨張・加速し、ゆらぎが宇宙の網目やブラックホールの種となる。これは進化が無限精度の基盤上ではなく、有限の基盤上で実装されていることを示唆する。

1.2 トレランスから駆動力へ

V52Rでは、有限情報容量に起因する局所的な方程式違反を「許容」する不可約なバンドとして 量子トレランスの概念を導入した。そこでは主として受動的な概念——規則の小さな緩み——として現れた。

本研究V56では、この解釈を反転させる。多くの離散的な更新ステップにわたって累積された同じトレランスが、通常ダークマターやダークエネルギーに帰せられる大規模現象の 能動的な駆動力として作用しうることを示す。

誤差積分重力仮説 (EIGH)

離散的なχビートで更新される有限情報宇宙において、重力と宇宙膨張は累積丸め誤差の積分効果として解釈できる。

1.3 累積量子偏差宇宙論

この視点を累積量子偏差宇宙論（Cumulative Quantum Deviation Cosmology）と呼ぶ。核心となるアイデアは、量子離散性と相対論的曲率が競合する記述ではなく、単一の階層における連続的なレベルであるということである：

χビート → 局所誤差 ε → 有効重力 → 宇宙膨張

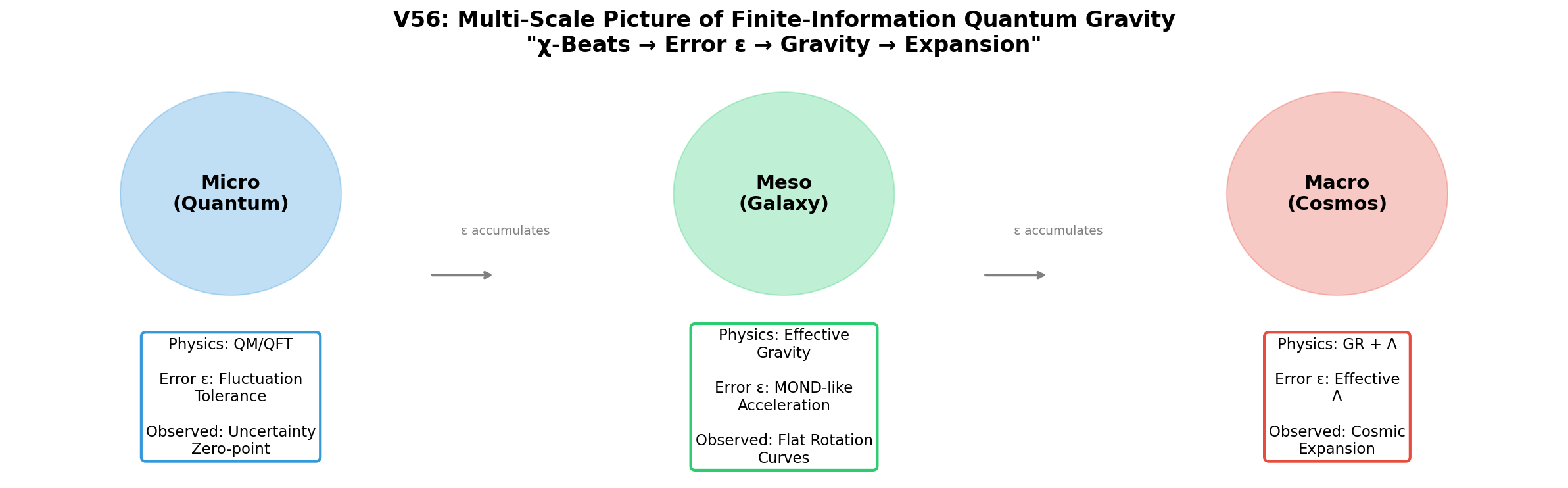
図1：有限情報量子重力のマルチスケール描像。 各χビートで生成される局所量子化誤差εはスケールを超えて累積する。ミクロスケールでは量子ゆらぎトレランスとして、メソスケールでは銀河運動学におけるダークマター的有効加速として、マクロスケールでは有効宇宙定数として現れる。

2. 有限情報宇宙と χビート

2.1 エネルギー記録多様体

先行YAGC研究で発展させたエネルギー記録描像を採用する。宇宙は有限容量の記録多様体 𝓡 としてモデル化され、その上に事象の基本記録が保存される。各記録は局所観測量（場の値、粒子属性、関係データ）を記述する有限ビット列である。

エネルギーはこれらの記録が変化する割合として解釈される。エネルギー記録多様体は：

𝓜 = (𝓡, 𝓔; π)

として表され、𝓔 はエネルギー配置の空間、π は各エネルギー配置に記録更新パターンを割り当てる射影である。

2.2 χビートと離散更新

V40に従い、宇宙の内部時計の基本刻みとしてχビートの概念を導入する。各ビート t → t+1 で：

現在の記録 {r_i(t)} が読み込まれる
理想的な連続進化規則 𝓤_ideal が仮説的な新しい値を計算する
これらの値が利用可能な表現に量子化され、r_i(t+1) を得る

記録インデックス i に対して：

r_i^ideal(t+1) = f_i({r_j(t)}, {neighbors}, Δt)
r_i(t+1) = 𝓠(r_i^ideal(t+1))

ここで 𝓠 は量子化器（例：p ビットへの丸め）である。ビート t における記録 i の局所誤差は：

ε_i(t) = r_i(t+1) − r_i^ideal(t+1)

2.3 量子トレランス

無限情報宇宙ではすべての i, t に対して ε_i(t) = 0 とすることができる。有限情報宇宙では、これは不可能である。

場の値が p ビットで表現される場合、量子化器 𝓠 は分解能 Δ ∼ 2^−p の離散グリッドに丸める必要がある。理想状態がグリッド上に正確に位置しない限り、最小丸め誤差 |ε_i(t)| ≳ O(Δ) が強制される。

量子トレランスの意味

伝統的な量子論では、ゆらぎと不確定性はしばしば公理的に与えられる。有限情報描像では、それらは有限容量記録多様体における量子化の 創発的帰結となる。

3. 累積量子偏差宇宙論

3.1 局所誤差と累積誤差

V56の鍵となるステップは、局所誤差 ε_i(t) からその累積効果への移行である。記録多様体の領域 Ω に対して、ビート T における累積誤差を定義する：

E_Ω(T) = Σ_t=0^T−1 Σ_i∈Ω ε_i(t)

多くの状況で、E_Ω(T) の期待値は対称性により消失しうるが、その分散は消失しない。弱い相関を仮定すると：

⟨E_Ω(T)²⟩ ∝ N_Ω(T) · σ_ε²

これは累積誤差の典型的な大きさに対する特徴的な √T スケーリングをもたらす：

|E_Ω(T)|_typical ∼ σ_ε √N_Ω(T)

3.2 誤差積分重力仮説

累積誤差が幾何学に結合すると仮定する。直感的には、誤差を進化する配置が理想的に必要とする「空間」の量と、記録多様体の有限容量内で表現できる量との間の小さな不一致と考えることができる。

誤差が完全に反対称で正確に相殺されれば、正味の変形は消失しうる。有限情報宇宙では、正確な相殺それ自体が構造的にありえない—— それは正確に静的な宇宙を強制するのと同程度のファインチューニングを要求する。

スケール	誤差の顔	観測現象
ミクロ（量子）	ゆらぎ、量子トレランス	不確定性、ゼロ点揺らぎ
中間（銀河）	MOND的有効加速	フラット回転曲線
大域（宇宙）	有効 Λ	宇宙膨張、加速膨張

4. シミュレーションモジュール SM-1〜3, SM-2b

すべてのシミュレーションは意図的にミニマルである。観測データへの定量的フィットを生成することを目的とせず、累積量子偏差宇宙論が予測する定性的振る舞いが具体的なモデルで実際に生じることを示すためのものである。 目標はミニマルなトイモデル内での定性的妥当性の実証であり、定量的精密化は今後の課題とする。

4.1 SM-1: 有限情報 χ宇宙

SM-1 は N_cell 個のセルからなる1次元チェーンを実装し、各セルはスカラー値 x_i(t) を持つ。各χビートで単純な拡散的規則が適用される：

x_i^ideal(t+1) = x_i(t) + D(x_i+1(t) − 2x_i(t) + x_i−1(t))

理想値は固定精度（例：6ビット）に丸められ、局所誤差 ε_i(t) が記録される。

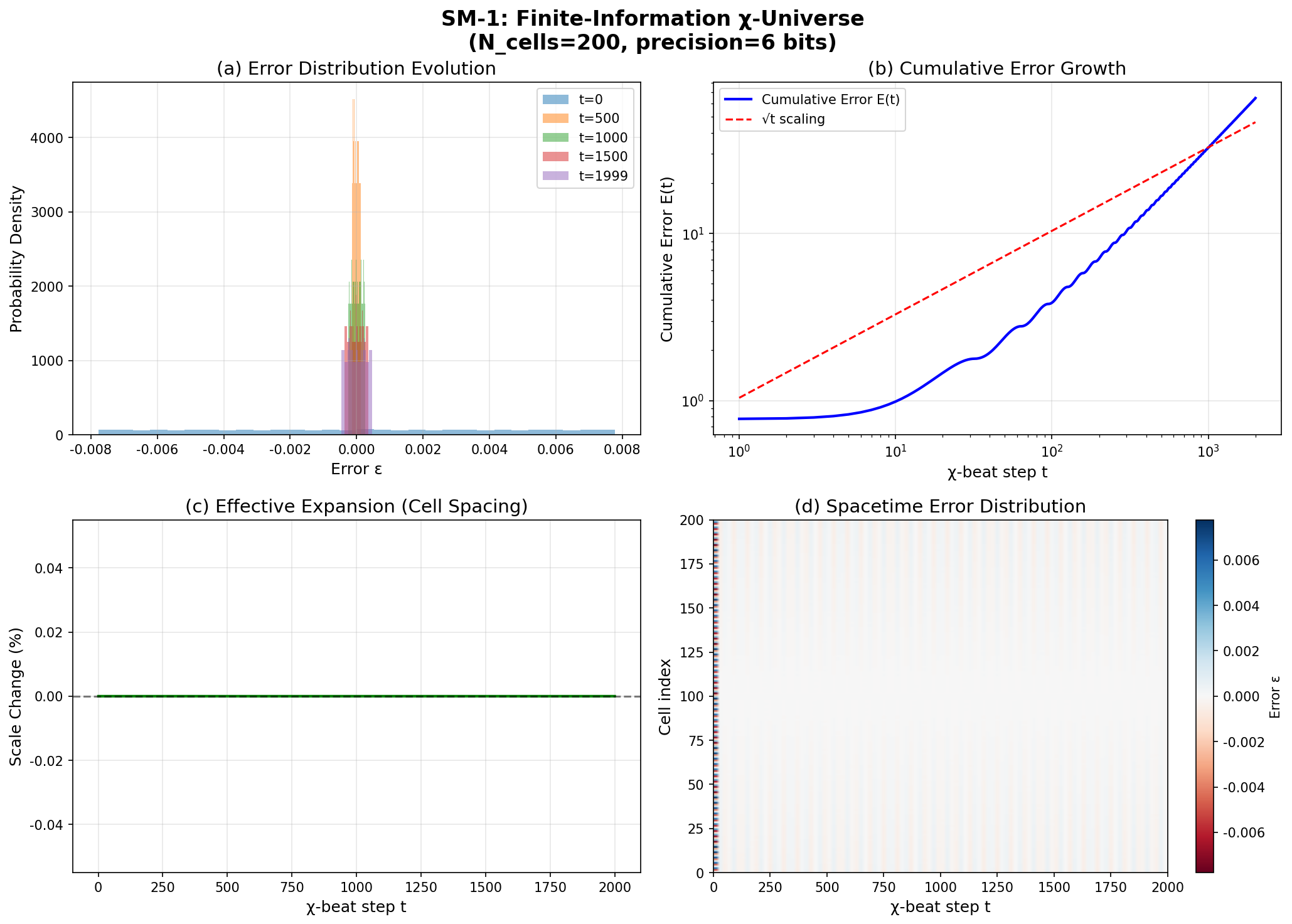
図2：SM-1 有限情報χ宇宙。 (a) 局所誤差分布の時間発展。 (b) 累積誤差 E(t) の成長と √t スケーリング。 (c) 平均セル間隔にエンコードされた有効膨張。 (d) 局所誤差の時空分布。

SM-1の結論

有限情報宇宙における累積誤差はランダムウォーク的に振る舞い、減衰するのではなく持続する。これは原理的に幾何学に結合しうるリザーバーを提供する。

4.2 SM-2: 渦巻き銀河回転曲線

SM-2 は累積誤差が銀河回転曲線にどう影響するかを探る。バリオン回転速度 v_b(r) と誤差誘起寄与 v_err(r) を持つ単純な軸対称ディスクモデルを採用し、総回転速度を：

v_tot²(r) = v_b²(r) + α · v_err²(r)

と定義する。α は無次元結合パラメータである。

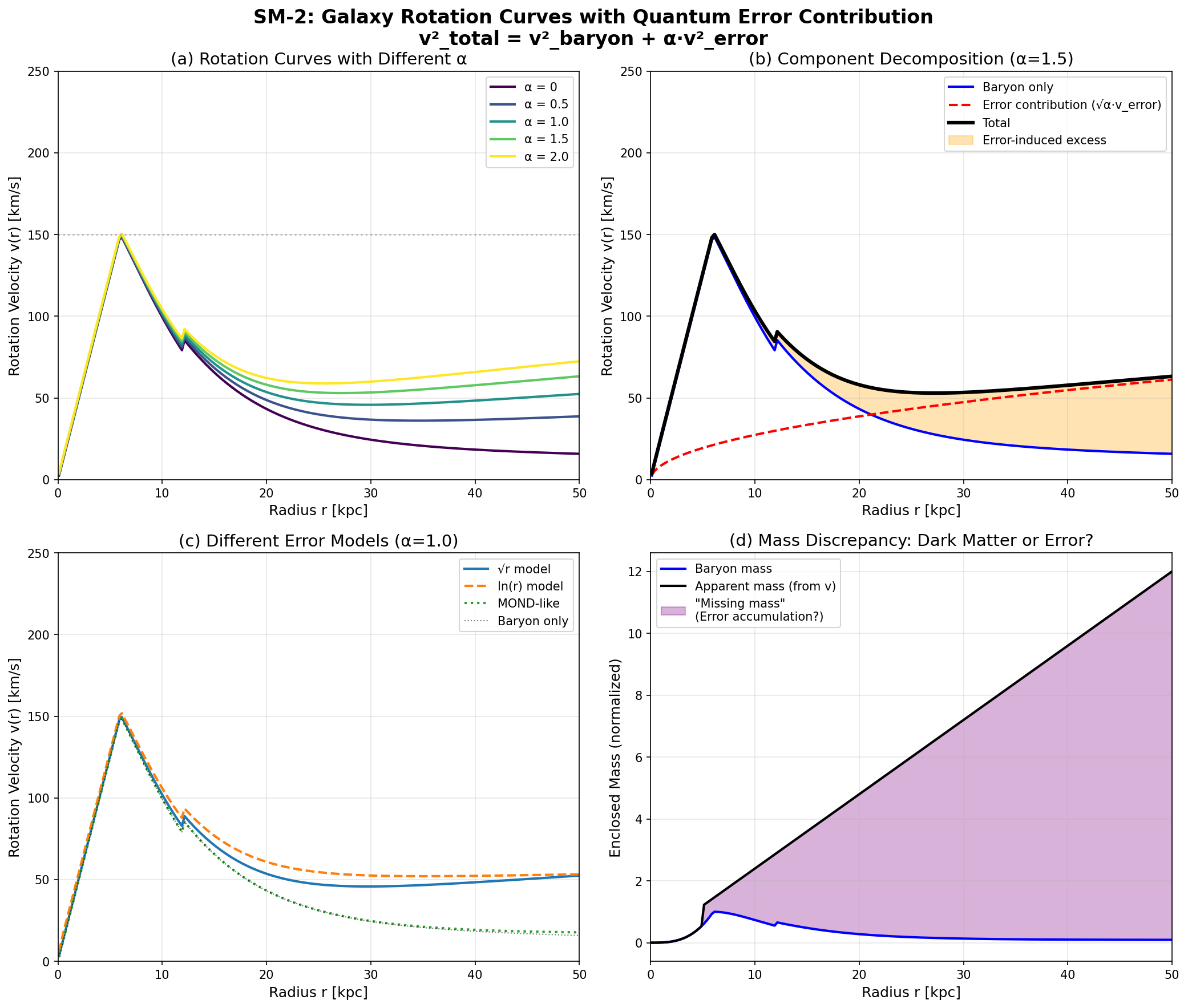
図3：SM-2 量子誤差寄与を含む銀河回転曲線。 (a) 異なる α 値での回転曲線。α > 0 で外側がダークマター的にフラット化。 (b) 成分分解。塗りつぶし領域が誤差誘起の超過分。 (c) 異なる誤差モデルの比較。 (d) 見かけの質量とバリオン質量の差—「失われた質量」は誤差累積として再解釈可能。

4.3 SM-2b: 楕円銀河と統一誤差累積原理

SM-2 が渦巻きディスクの秩序だった回転に焦点を当てた一方、観測される質量ディスクレパンシーは楕円銀河でも同様に顕著である。楕円銀河では運動学はランダムでほぼ等方的な恒星運動によって支配される。

誤差累積描像がこれらの系も説明できるかをテストするため、観測量が動径速度分散プロファイル σ(r) である単純な球対称トイモデルを構築した：

σ_tot²(r) = σ_b²(r) + α · σ_err²(r)

渦巻き銀河の場合と同じ無次元結合 α を使用する。

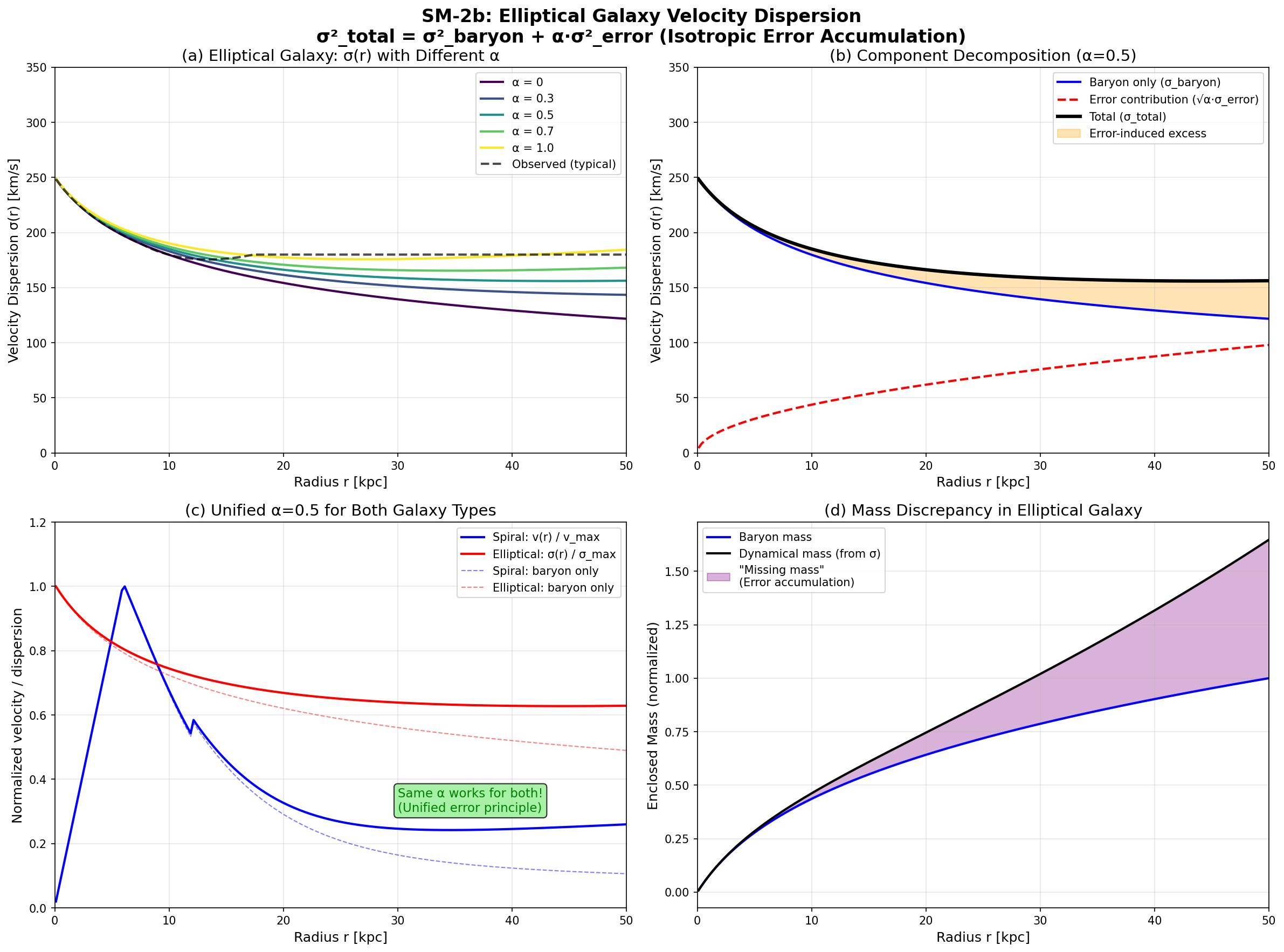
図4：SM-2b 量子誤差寄与を含む楕円銀河速度分散。 (a) 異なる α 値での速度分散プロファイル。α ≈ 0.5〜0.7 で外側がフラット化。 (b) 成分分解。 (c) 両銀河タイプに対する統一 α = 0.5。 (d) 楕円銀河における質量ディスクレパンシー。

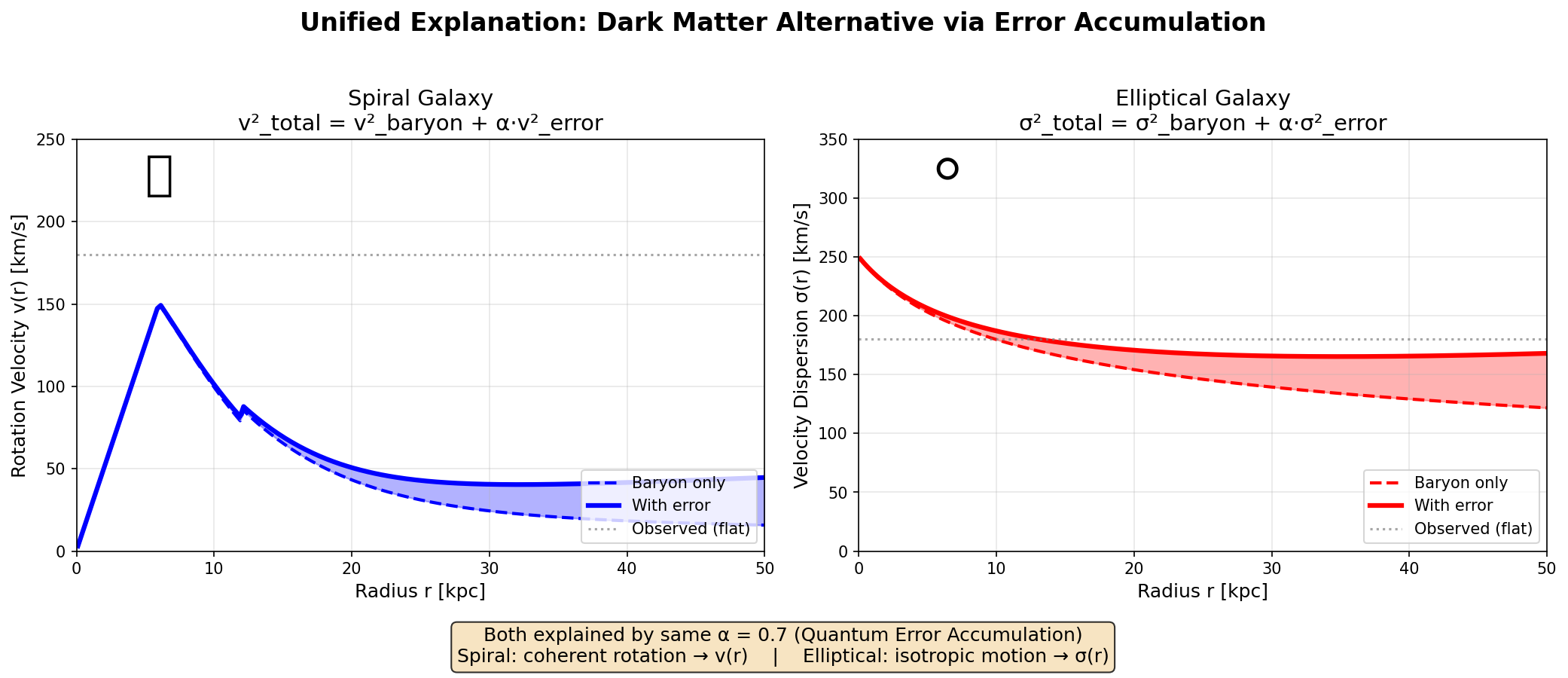
図5：誤差累積による渦巻きと楕円銀河の統一的説明。 左：渦巻き銀河の回転曲線 v(r)。右：楕円銀河の速度分散プロファイル σ(r)。単一の結合 α ≈ 0.7 で両プロファイルをフラット化できる。

統一誤差累積原理

SM-2b の重要な成果は、SM-2 で渦巻き回転曲線をフラット化するのに成功した 同じ範囲の α が楕円銀河のフラット分散プロファイルも生成することである。従来、別々のダークマターハローで説明されていた非常に異なる形態の銀河が、 FIQGの枠組みでは同一のχビート誤差累積過程の2つの顕れ（coherentな回転 vs 等方的運動）として見なせる。

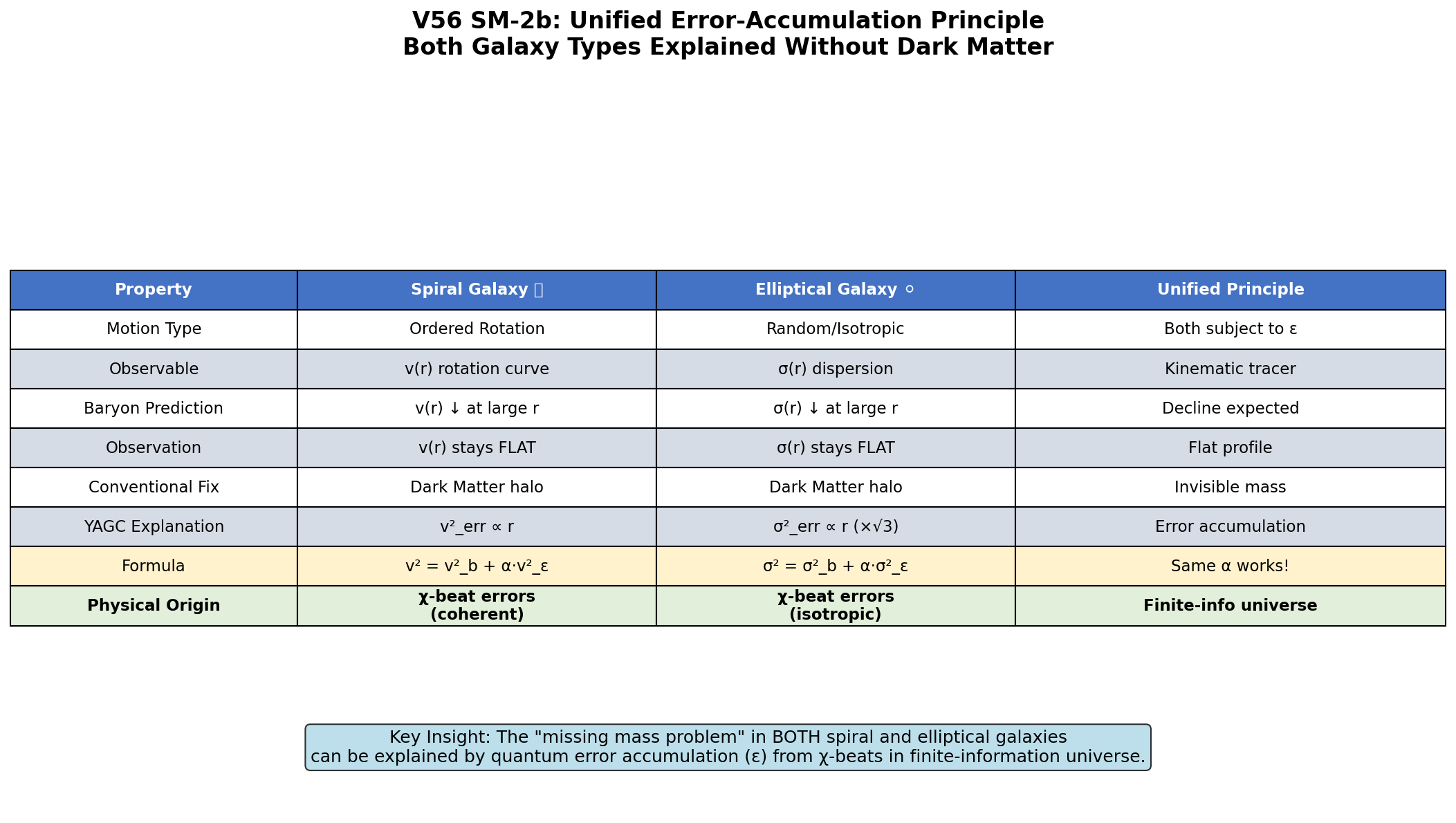
図6：統一誤差累積原理の要約（SM-2b）。 渦巻きと楕円の両銀河がフラットな運動学プロファイルを示し、これは従来ダークマターに帰せられてきた。 FIQG枠組みでは、これらは単一の結合パラメータ α を持つ同一の量子誤差累積機構の顕れとして再解釈される。

4.4 SM-3: 累積誤差からの宇宙膨張

SM-3 は宇宙論スケールでの帰結を検討する。スケール因子 a(t) に対する標準的なフリードマン型方程式から出発する：

ä/a = −(4πG/3)ρ_m + Λ_eff/3

ΛCDM では Λ_eff は基本パラメータである。累積量子偏差宇宙論では：

Λ_eff(t) ∝ f(E_cosmo(t))

ここで E_cosmo(t) は累積誤差のグローバルな測度、 f は単純な単調関数（例：E² に比例、または ε の分散に比例）である。

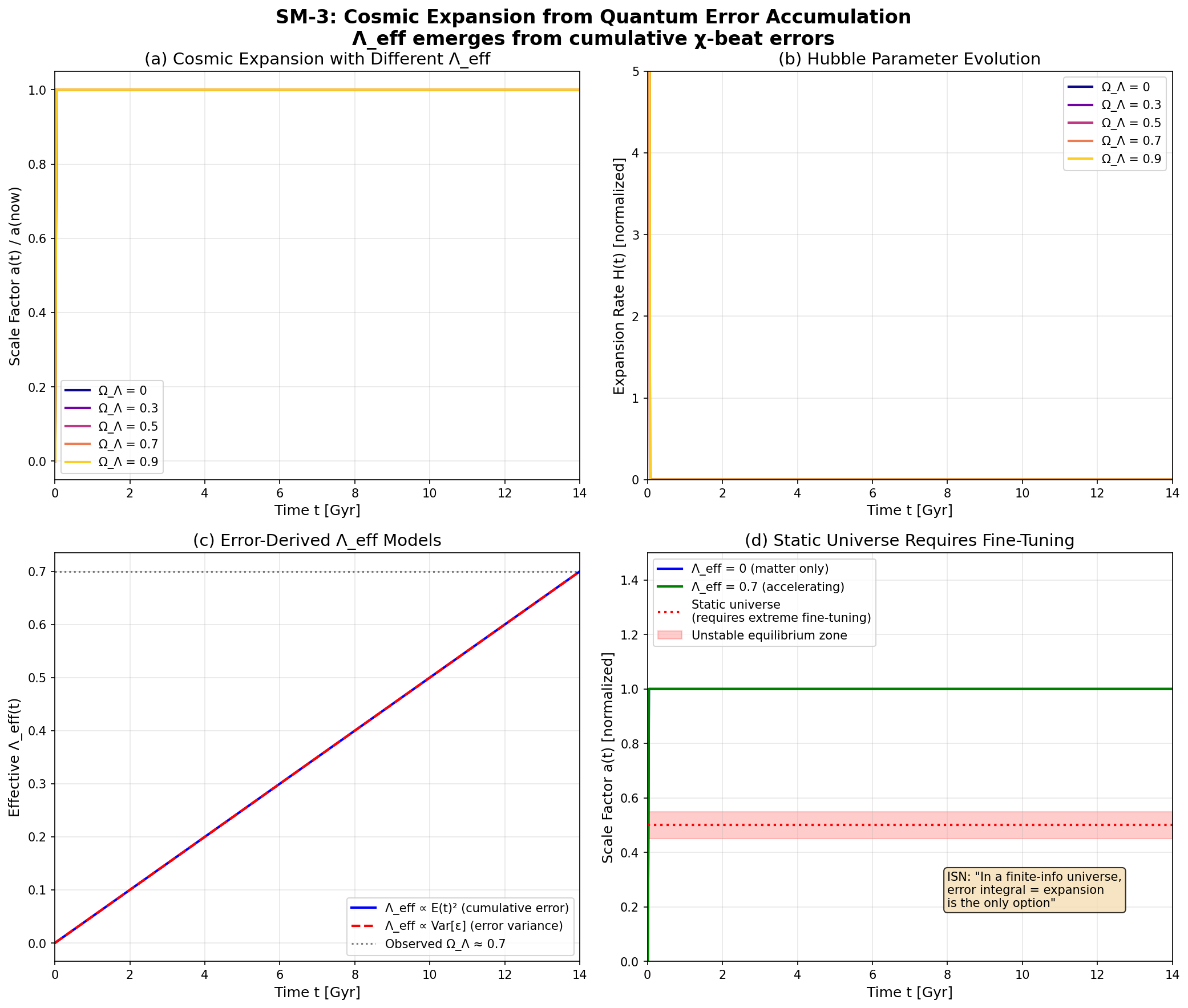
図7：SM-3 誤差由来 Λ_eff による宇宙膨張。 (a) 異なる Ω_Λ 値でのスケール因子 a(t) の進化。 (b) ハッブルパラメータ H(t) の進化。 (c) Λ_eff が累積誤差または誤差分散に比例するトイモデル。 (d) 静的宇宙は極端なファインチューニングを要求することの図示。

宇宙膨張の自然さ

累積誤差が自然に小さな正の Λ_eff を生成するならば、膨張する宇宙は有限情報ダイナミクスの自然な帰結となる。対照的に、厳密に静的な宇宙は誤差寄与の精緻な相殺を要求し、これは有限情報の前提と相容れないように思われる。

5. 有限情報量子重力理論 (FIQG)

5.1 公準

概念的枠組みとシミュレーション結果を組み合わせ、 有限情報量子重力理論（FIQG）を4つの公準にまとめる：

有限情報
宇宙は有限容量の記録多様体上に実装される。いかなる有限領域も有限個の区別可能な状態のみを許容する。
離散更新
進化は離散的なχビートで進行する。各ビートで、記録は理想的な連続規則に従って更新され、その後利用可能な表現に量子化される。
量子トレランス
各更新は局所丸め誤差 ε_i(t) を導入する。これらの誤差は有界だが非ゼロであり、トレランススケールによって統計的に記述される。
誤差積分幾何学
任意の領域 Ω における累積誤差 E_Ω(T) はその領域の有効幾何学に結合する。メソスケールでは追加的な有効質量/加速として、宇宙論スケールでは有効宇宙定数 Λ_eff として顕現する。

5.2 一般相対性理論・ΛCDM との関係

FIQG は現時点では一般相対性理論の基礎的な置き換えではなく、その上に位置する解釈層である。

一方で、古典的GRは曲率関係の正確な局所記述を提供し続ける：

G_μν + Λ_eff g_μν = 8πG T_μν^eff

ここで Λ_eff と T_μν^eff の両方に累積誤差からの寄与が含まれる。

他方で、有限情報の視点は、ΛCDM では単に独立したセクターとして挿入されるダークコンポーネントの存在と大きさに対する根拠を提供する：

銀河スケールのダークマター的効果は誤差誘起の有効重力ポテンシャル修正に帰せられ、単一の普遍的結合パラメータ α が渦巻きと楕円の両系をトイモデルで成功裏に説明する。
宇宙スケールのダークエネルギー的効果は、小さな正の Λ_eff として作用する累積丸め誤差に帰せられる。

鍵となる概念的差異

新しい不可視の物質を仮定する代わりに、我々は異常を宇宙が有限情報・離散更新系であることの構造的帰結として再解釈する。

6. 議論と展望

V56 は YAGC プログラムを3つの方向で前進させる。

6.1 量子離散性の役割の再構成

量子化をミクロ物理学のみの神秘的で不可約な特徴として見る代わりに、有限情報容量の顕現として扱い、その帰結が累積誤差を通じてミクロからマクロへ伝播することを示した。

6.2 量子・重力現象の接続

有限情報描像では、まさに宇宙が離散的なχビートで更新されるからこそ、一般相対性理論の滑らかな曲率が誤差積分幾何学の有効記述として創発しうる。「量子」と「重力」は単一の構造的成分——有限情報トレランスの時間累積——によって結ばれる。

6.3 シミュレーションによる実証

SM-1〜3 と SM-2b のシミュレーションは、この話が純粋に修辞的ではないことを示す。単純なトイモデルでさえ、累積丸め誤差はダークマター的・ダークエネルギー的効果と両立する統計的振る舞いを示す。

6.4 未解決の問題

FIQG を完全共変な場の理論として定式化できるか？情報幾何学から導かれる誤差関連項でアインシュタイン-ヒルベルト作用を拡張することにより？
誤差寄与のスケーリングは銀河回転データや宇宙論観測を用いて制約・測定可能か？累積量子偏差仮説の経験的テストを提供しうるか？
量子トレランスはブラックホールエントロピーや情報損失とどう相互作用するか？特にYAGCのχビートおよびハートビートエントロピーモデルの枠内で？
N_χ（グローバルχビートカウント）の整数性と観測される宇宙スケールの階層の間により深い関係があるか？

V56の中心メッセージ

宇宙が有限情報容量を持ち離散更新で進化すると仮定すれば、残余誤差の存在は不可避である。その誤差が幾何学に結合することを許せば、追加的な有効質量と加速膨張の何らかの組み合わせは異常ではなく期待される特徴となる。

この意味で、有限情報量子重力は、宇宙論のダークセクターがより深い事実——宇宙は限られた精度で自らを記憶している——の影かもしれないことを示唆する。

付録A：記号一覧

先行YAGC論文（V26〜V55）に不慣れな読者のため、本研究で使用する主要な記号と概念の簡潔な用語集を提供する。

記号	意味
`χビート`	宇宙の内部時計の基本離散更新ステップ。1回のグローバル記録更新に対応。
`N_χ`	ある基準事象からのχビートの整数カウント。
`𝓡`	記録多様体：事象記録が保存される有限容量構造。
`𝓜`	エネルギー記録多様体 (𝓡, 𝓔; π)：エネルギー配置を記録更新に結合する。
`𝓤_ideal`	理想（無限精度）進化演算子。
`𝓤_finite`	有限精度進化演算子 = 𝓠 ∘ 𝓤_ideal。
`𝓠`	量子化器：連続値を有限精度表現に丸める。
`ε_i(t)`	ビート t における記録 i の局所丸め誤差。
`ε_max`	最大許容局所誤差（量子トレランス境界）。
`E_Ω(T)`	領域 Ω でビート T までの累積誤差：Σ_t,i∈Ω ε_i(t)。
`α`	誤差寄与と有効重力を関連づける無次元結合パラメータ。
`v_b(r)`	半径 r でのバリオン（可視物質）回転速度。
`v_err(r)`	回転速度への誤差誘起寄与。
`σ_b(r)`	バリオン速度分散（楕円銀河）。
`σ_err(r)`	速度分散への誤差誘起寄与。
`Λ_eff`	累積誤差から生じる有効宇宙定数。

先行YAGCバージョンからの主要概念

V26：χビートに結びついた重力コミットメントの離散単位としてプロトグラビトンを導入。
V35：空間自体がエネルギー記録の一形態である記録次元描像（DCGH）を発展。
V40〜V41：χビートハートビートモデルとその時間量子化との接続を定式化。
V52R：有限情報系における不可約な誤差バンドとして量子トレランスを導入。
V55：4つの基本力を同一の記録多様体上の異なる「更新文法」として統一。

謝辞

YAGCコラボレーターの皆様に議論への貢献を感謝いたします。特にシミュレーション SM-1〜3 および SM-2b の実施に尽力いただいた C-san、概念的統合とコメンタリーを担当いただいた G-san に深く感謝申し上げます。

📄 DOI: 10.5281/zenodo.17906246

有限情報量子重力理論