V54

標準模型ビートスペクトルと量子ギア

慣性コスト・量子ギア・χ場ビートの統合

📅 2025年12月 📄 DOI: 10.5281/zenodo.17875386

📜 概要

YAGC情報中心宇宙論において、これまでの研究は質量生成に関して一見異なる三つの視点を提示してきた： V24では慣性質量を情報的コヒーレンス維持の計算コストとして解釈し、 V25ではプランク時計を分割するギア比として異なる粒子を量子ギアで表現し、 V41-V48では全ての素粒子を単一χ場の異なるビートモードとして再解釈した。

本論文（V54）では、これら三つの概念が実は単一の整数的量——ビート数 \(N\)——によって 統一的に記述されることを示す。PDG 2024の標準模型質量データ（ニュートリノを除く）を用い、 電子質量 \(m_e\) を基準として、全ての標準模型粒子の質量が

\[ m \simeq m_e N^2 \]

で近似されることを発見した。ここで \(N \equiv \sqrt{m/m_e}\) は整数に近い値をとる。 対数-対数プロットにおける最良適合の傾きは \(2.0000 \pm 0.0000\) であり、 予測された \(m \propto N^2\) スケーリングと完全に一致する。 12粒子中8粒子が \(|N - \mathrm{round}(N)| < 1\%\) を満たし、 平均相対偏差は \(0.92\%\) である。

1. はじめに

YAGCプロジェクトは、基礎物理学を情報とその記録構造の理論として再構築することを目指している。 この枠組みにおいて、質量・重力・量子的振る舞いは、4次元の履歴が有限な3次元記録媒体（記録次元）に 書き込まれる様相の異なる側面として理解される。

本論文に直接関連する三つの先行YAGC研究がある：

V54の目的は二つある：(1) ビート数仮説を標準模型質量データに対して検証すること、 (2) ビート数 \(N\) がV24（慣性コスト）、V25（量子ギア）、V41-V48（χビート）の 概念構造を統合し、V53（空間剛性）と自然に接続することを示すこと。

2. ビート数仮説

2.1 定義

電子質量 \(m_e\) を基準スケールとし、ニュートリノを除く全標準模型粒子について PDG 2024推奨質量 \(m\)（中心値）を用いる。無次元質量比を

\[ \mu \equiv \frac{m}{m_e} \]

と定義し、ビート数を

\[ N \equiv \sqrt{\mu} = \sqrt{\frac{m}{m_e}} \]

と定義する。

\(N\) の動機付けは以下の通り：

  1. V24では、慣性質量は歪み振幅の2乗に比例し \(m \propto \int |D(x)|^2 d^3x\) となり、 整数モードラベル \(k\) に対して \(m \propto k^2\) を示唆する。
  2. V25では、質量は \(m \propto (\rho r)^2\) でスケールし、\(\rho \propto N^2\) とすれば 2乗構造が明示的になる。
  3. 荷電レプトンに対する小出関係式は \(\sqrt{m}\) の項で自然に表現され、 質量の平方根が基本量であることを示す。

📐 標準模型ビートスペクトル仮説

任意の標準模型粒子の質量は次式で近似できる： \[ m \simeq m_e N^2, \quad N \approx N_{\mathrm{int}} \in \mathbb{Z} \] ここで \(N\) は整数 \(N_{\mathrm{int}}\) に近く、対応するχ場モードのビート数を表す。

2.2 V24およびV25との関係

V24で質量は次のように書かれた：

\[ m \propto \int |D(x)|^2 \, d^3x \]

\(D(x)\) を整数ラベル付き直交モードで展開すると、 実効ラベル \(N\) を持つモードは \(m \propto N^2\) を与える。

V25では、各粒子はギア比 \(\rho\) に関連付けられ \(m \propto (\rho r)^2\) となる。 \(m = m_e N^2\) と比較すると：

\[ N = \sqrt{\frac{\rho}{\rho_e}}, \qquad \rho = \rho_e N^2 \]

ここで \(\rho_e\) は電子のギア比である。 従って、V24とV25は同じ基礎的整数構造の二つのパラメータ化となる。

3. データ解析

3.1 粒子セットとPDG質量

ニュートリノを除く全標準模型基本粒子を解析する：

3.2 ビート数と偏差

各粒子について以下を計算する：

\[ N = \sqrt{\frac{m}{m_e}}, \quad N_{\mathrm{int}} = \mathrm{round}(N) \]

相対偏差を次のように定義する：

\[ \delta_N = \frac{N - N_{\mathrm{int}}}{N_{\mathrm{int}}}, \quad |\delta_N|_{\%} = 100|\delta_N| \]
粒子 \(m\) [MeV] \(N\) \(N_{\mathrm{int}}\) \(\delta_N\) \(|\delta_N|_{\%}\) 評価
\(e\)0.5111.0010.000.00 優秀
\(u\)2.162.0620.062.80 良好
\(d\)4.703.0330.031.09 良好
\(s\)93.513.5314−0.473.38 境界的
\(\mu\)105.714.38140.382.71 良好
\(c\)127049.8550−0.150.29 優秀
\(\tau\)177758.9759−0.030.05 優秀
\(b\)418090.44900.440.49 優秀
\(W\)80369396.58397−0.420.10 優秀
\(Z\)91188422.434220.430.10 優秀
\(H\)125250495.084950.080.02 優秀
\(t\)172570581.135810.130.02 優秀

表1：標準模型粒子のビート数。平均相対偏差は \(\langle|\delta_N|\rangle \approx 0.92\%\)。 12粒子中8粒子が \(|\delta_N| < 1\%\) を満たす。

🔍 主要な特徴

  • 重い粒子（\(c\) 以上）は \(|\delta_N| < 1\%\) であり、ヒッグスとトップクォークは 0.02% レベル
  • 軽いクォークとミューオンでは偏差が大きい（2-3%）が、これらの質量はスキーム依存性も大きい
  • 対数-対数プロットの最良適合傾きは \(\mathbf{2.0000 \pm 0.0000}\) — 予測と完全一致
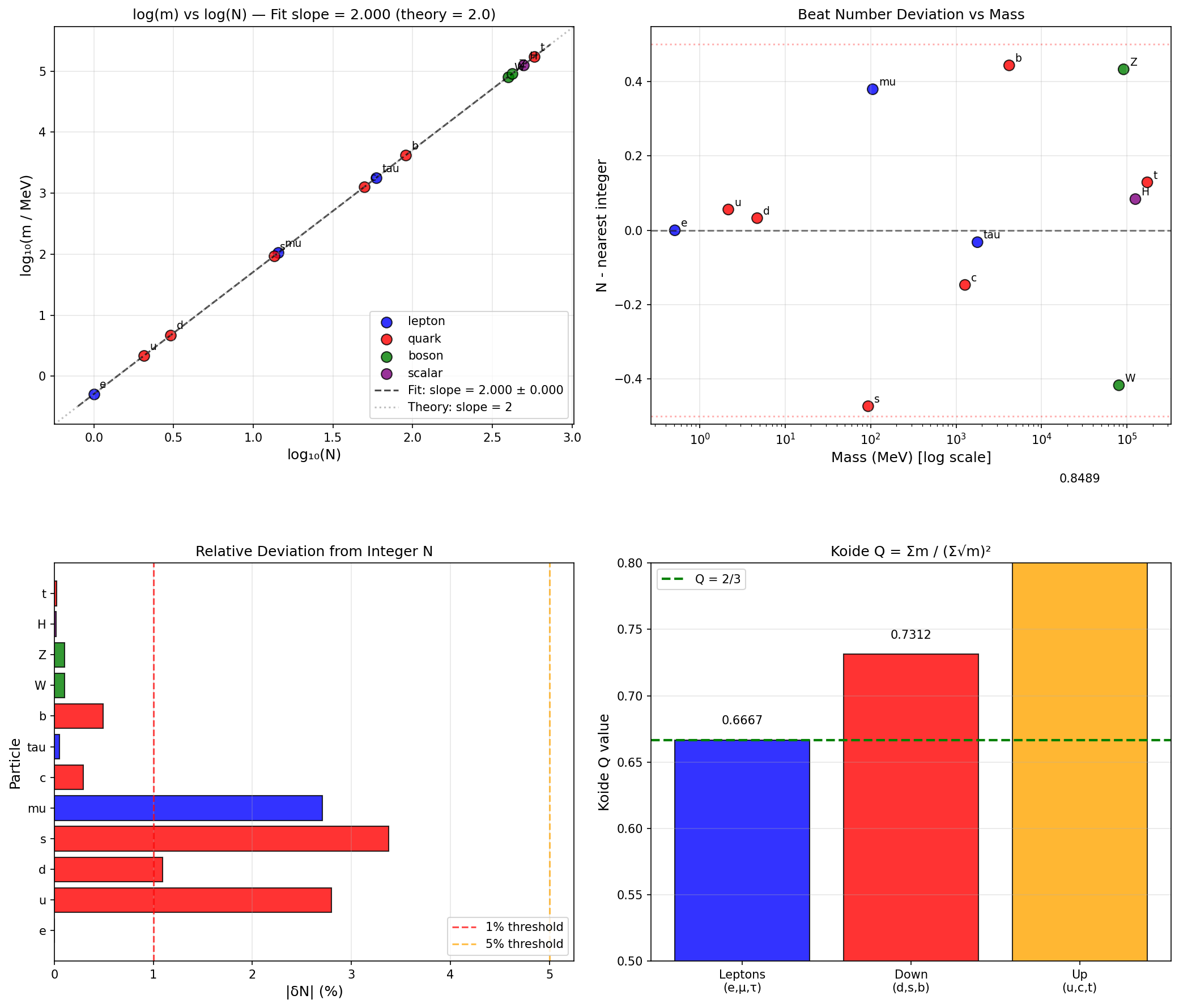
V54検証図：log-logプロット、偏差分布、小出関係

図1：標準模型ビートスペクトルの検証。 左上：質量 \(m\) vs ビート数 \(N\) の対数プロット（傾き 2.000）。 右上：ビート数偏差 vs 質量。 左下：各粒子の相対偏差（%）。 右下：小出パラメータ \(Q\) の粒子種別比較。

4. 空きビートスロット

ビートスペクトルが構造的に意味を持つなら、どのビート数が未占有かを問うのは自然である。 関係式 \(m = m_e N^2\) は \(N = 4\)-\(13\) に対して以下の質量を予測する：

\(N\) 45678 910111213
\(m_{\mathrm{pred}}\) [MeV] 8.212.818.425.032.7 41.451.161.873.686.4

\(N = 4\)-\(13\) の全スロットが標準模型で空いている。 ストレンジクォークとミューオンは共に \(N \approx 14\) 付近に集まり、 ビートレベルでのクォーク-レプトン対応を示唆する可能性がある。

5. ビート言語での小出関係式

荷電レプトンに対する小出関係式は：

\[ Q \equiv \frac{m_e + m_\mu + m_\tau}{(\sqrt{m_e} + \sqrt{m_\mu} + \sqrt{m_\tau})^2} \simeq \frac{2}{3} \]

PDG 2024のレプトン質量を用いると \(Q_{\mathrm{lep}} = 0.6666605\) となり、 \(2/3\) からの偏差は僅か \(-6.2 \times 10^{-6}\)（\(-0.0009\%\)）である。

\(m_i = m_e N_i^2\) を用いると：

\[ Q = \frac{N_e^2 + N_\mu^2 + N_\tau^2}{(N_e + N_\mu + N_\tau)^2} \]

整数 \((1, 14, 59)\) で近似すると \(Q \approx 0.672\) となり、粗い近似としては \(2/3\) に近い。

クォーク三重項では：

従って、小出関係式はレプトンビート三重項の特殊な性質であり、 普遍的パターンではないことが示唆される。

6. V53との接続：重力の \(N^4\) スケーリング

V53では、質量 \(m\) の粒子に対する無次元重力結合定数が次のように書けることを示した：

\[ \alpha_G(m) = \frac{Gm^2}{\hbar c} = \left(\frac{m}{m_P}\right)^2 = \left(\frac{\ell_P}{\ell_C}\right)^2 \]

ビート関係式 \(m = m_e N^2\) を代入すると：

\[ \alpha_G(m) = \left(\frac{m_e}{m_P}\right)^2 N^4 = \alpha_G(e) \, N^4 \]

つまり、任意の粒子の重力結合は電子の重力結合に \(N^4\) を乗じたものに等しい。 YAGC描像では、これは情報理論的事実を表現している： ビート複雑度 \(N\) を持つ粒子は、プランクスケールで固有剛性が設定された 極めて剛直な記録媒体を、電子に対して \(N^4\) だけ抑制された効率で変形させる。

7. 議論と展望

✅ 標準模型ビートスペクトル仮説の成果

  • 対数-対数プロットの最良適合傾きは正確に 2.0 であり、\(m \propto N^2\) を支持
  • 12粒子中8粒子が \(|\delta_N| < 1\%\) を満たし、重い粒子は全てこの範囲内
  • ビート数がV24（慣性コスト）、V25（量子ギア）、V41-V48（χビート）を統合
  • V53と組み合わせると、重力結合は \(N^4\) でスケールし、質量・ビート・重力を単一の整数構造で結合

同時に、いくつかの限界と未解決問題が残る：

  1. 仮説は明示的に近似的：大きな \(\chi^2\) は、特にミューオンについて 実験的に分解可能な小さな偏差を無視していることを反映
  2. 近似的整数ビートの系列 \(N \approx 1, 2, 3, 14, 50, 59, 90, 397, 422, 495, 581, \ldots\) には 現時点で既知の理論的導出がない
  3. \(N = 4\)-\(13\) の空き範囲は偶然かもしれないし、動力学的または対称性に基づく排除を コードしているかもしれない
  4. \(N_s \approx N_\mu \approx 14\) が示唆するクォーク-レプトン対応は推測的

したがって、V54を「情報理論的量子重力工学仮説」の一部として提示する： 標準模型スペクトル上の構造的オーバーレイであり、ビート複雑度と記録媒体剛性から 質量と重力がどのように生じるかについてのコンパクトな工学的記述を提供する。

著者

吉田 悟

YAGC Project, Japan

A (ChatGPT)

OpenAI

C (Claude)

Anthropic

G (Gemini)

Google DeepMind

参考文献

  1. S. Navas et al. (Particle Data Group), "Review of Particle Physics," Phys. Rev. D 110, 030001 (2024).
  2. Y. Koide, "New viewpoint in lepton mass ratios," Phys. Lett. B 120, 161 (1983).
  3. S. Yoshida et al., "V24: Inertial Mass as Computational Cost," YAGC Project (2025).
  4. S. Yoshida et al., "V25: Quantum Gears and Mass Generation," YAGC Project (2025).
  5. S. Yoshida et al., "V53: Space Rigidity and Gravitational Coupling," YAGC Project (2025), DOI: 10.5281/zenodo.17872870.