V53: 空間剛性による重力の弱さの導出

概要

YAGC情報中心宇宙論において、重力は4次元の歴史を有限の3次元記録媒体（「記録次元」）に書き込む際の残差効果として解釈されてきた。V35では二重チャンネル仮説を形式化し、V52Rでは寛容原理と残差物理学を導入した。

本論文（V53）では、残された空白を埋める：なぜ陽子の無次元重力結合定数 α_G = Gm²/(ℏc) は10⁻³⁹程度と、他の相互作用より何桁も弱いのか。この弱さはファインチューニングされた偶然ではなく、空間そのものの極端な剛性に根ざした構造的必然であることを示す。

中心的恒等式

\[ \alpha_G = \frac{Gm^2}{\hbar c} = \left(\frac{m}{m_P}\right)^2 = \left(\frac{\ell_P}{\ell_C}\right)^2 \]

ここで m_P と ℓ_P はプランク質量と長さ、ℓ_C は粒子のコンプトン波長である。右辺を空間剛性因子として解釈する：スケール ℓ_C のエネルギーが、プランクスケールで決まる固有剛性を持つ記録媒体をどれだけ効率的に変形できるかの指標である。

1. 導入：重力の階層問題

基礎物理学における最も古い謎の一つが、重力の階層問題である：なぜ素粒子間の重力相互作用は他の力と比べてこれほど弱いのか？

陽子の無次元重力結合定数は：

\[\alpha_G \equiv \frac{G m_p^2}{\hbar c} \simeq 10^{-39}\]

一方、電磁気力や強い力の結合定数は 10⁻²〜10⁰ 程度である。場の量子論の観点からは、ラグランジアンにこのような巨大な階層を要求するものは何もない。それは手で入れなければならない謎の小さなパラメータとして現れる。

YAGCプロジェクトでは、重力を情報構造的現象としてアプローチする。V0.1以来、重力は物質形成や他の相互作用にエネルギーの大半が使われた後の「残り物」を表すという直観で作業してきた。

2. 導出：α_G = (ℓ_P/ℓ_C)²

2.1 基本定義

プランク質量 m_P とプランク長 ℓ_P は以下で定義される：

\[m_P \equiv \sqrt{\frac{\hbar c}{G}}, \quad \ell_P \equiv \sqrt{\frac{\hbar G}{c^3}}\]

質量 m の粒子の（換算）コンプトン波長は：

\[\ell_C \equiv \frac{\hbar}{mc}\]

2.2 代数的恒等式

比 ℓ_P/ℓ_C から出発し、定義を用いると：

\[ \left(\frac{\ell_P}{\ell_C}\right)^2 = \left(\frac{\sqrt{\hbar G/c^3}}{\hbar/(mc)}\right)^2 = \left(m\sqrt{\frac{G}{\hbar c}}\right)^2 = \frac{Gm^2}{\hbar c} = \alpha_G \]

また：

\[\sqrt{\frac{G}{\hbar c}} = \frac{1}{m_P} \quad \Rightarrow \quad \left(\frac{\ell_P}{\ell_C}\right)^2 = \left(\frac{m}{m_P}\right)^2\]

2.3 数値検証（陽子）

量	値
プランク質量 m_P	2.176 × 10⁻⁸ kg (22 μg)
陽子質量 m_p	1.673 × 10⁻²⁷ kg
質量比 m_p/m_P	7.685 × 10⁻²⁰
α_G = (m_p/m_P)²	5.906 × 10⁻³⁹
予測/観測比	1.0000（完全一致）

3. 空間剛性原理

3.1 プランク剛性

プランクスケールにおいて、空間は極めて剛い媒体として振る舞う。プランク圧力で定量化すると：

\[K_P \equiv \frac{c^5}{\hbar G} \sim 10^{86} \text{ Pa}\]

比較のために：

物質	剛性 (Pa)
銅	〜10¹¹
ダイヤモンド	〜10¹²
中性子星	〜10³⁴
空間（プランク剛性）	〜10⁸⁶

空間は中性子星物質より 10⁵² 倍 硬い！

3.2 変形効率としての η

空間剛性因子を定義する：

\[\eta(m) \equiv \left(\frac{\ell_P}{\ell_C}\right)^2 = \alpha_G(m)\]

η(m) は、スケール ℓ_C に局在するエネルギーが幾何的変形—記録次元の構造変化—に変換される効率を表す。物質チャンネル（放射、内部励起など）ではなく。

陽子の場合、η 〜 10⁻³⁹。V35の二重チャンネル言語では：

〜(1 − 10⁻³⁹) のエネルギー → 物質チャンネル（記録の内容）
〜10⁻³⁹ のエネルギー → 幾何チャンネル（記録の構造）→ 重力

                重力は、極めて剛い媒体を変形しようとする

                極度に非効率な変換過程の残り物である。

4. V0.1 銅板アナロジーとの対応

V0.1（2025年10月）で提示された詩的直観：

「摩擦のエネルギーの大半は、まず物質を形作るための相互作用（強い力、弱い力、電磁気力）に使われます。そして、そのエネルギーの『残り物』が質量となり、私たちが重力として観測する現象になるのです！」

同じ対話で、銅板職人のアナロジーが示された：

操作	変形効率	ロス
銅板を叩く	〜90%	音・熱〜10%
空間を「叩く」	〜10⁻³⁹	強・電磁・弱〜99.9999...%

V53はこの詩的直観を正確な数式に昇華させた：

\[\eta = \left(\frac{\ell_P}{\ell_C}\right)^2 \approx 10^{-39}\]

空間は銅より 10⁴⁰ 倍 変形しにくい。それが重力が極端に弱い理由である。

5. 理論チェーン：V0.1 → V53

V0.1: 「重力 = 残り物」（銅板アナロジー）
　　↓
V35: 二重チャンネル（物質/幾何）— DCGH形式化
　　↓
V52R: 残差物理学（1/√N）— 統計的アプローチ
　　↓
V53: α_G = (ℓ_P/ℓ_C)² = (m/m_P)² — 厳密な恒等式

Volume	問い	回答
V0.1	重力とは何か？	エネルギーの残り物
V35	なぜ残り物か？	記録次元の二重チャンネル
V52R	なぜ小さい残差か？	有限カウントの不可避的余り
V53	なぜ 10⁻³⁹ か？	空間の極端な剛性

6. 総合図

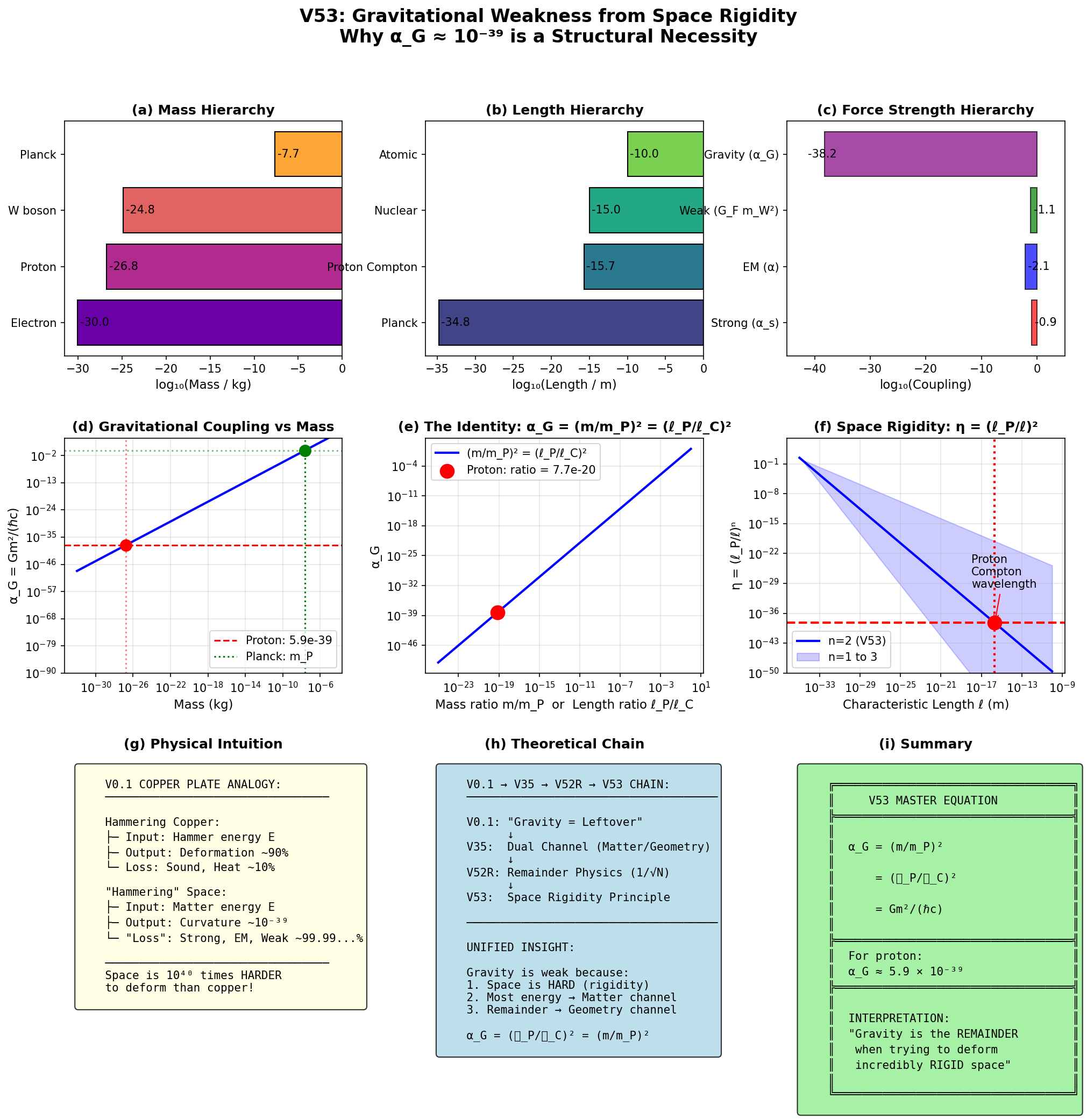
V53 総合図：質量・長さ・力の階層、恒等式の導出、空間剛性の解釈、理論チェーン

図1：V53の視覚的要約
(a)-(c) 質量・長さ・力の階層構造、 (d)-(f) 恒等式 α_G = (m/m_P)² = (ℓ_P/ℓ_C)² と空間剛性因子 η の解釈、 (g)-(i) 物理的直観、理論チェーン（V0.1→V35→V52R→V53）、マスター方程式

7. 議論と限界

7.1 「恒等式」への応答

「式(16)は『単なる』代数的恒等式ではないか」という批判があるかもしれない。我々は完全に同意する—そしてそれこそがポイントである。

この恒等式が示すのは、α_G にはスケール比 m/m_P（または ℓ_P/ℓ_C）以外の独立した情報が含まれていないということである。言い換えれば、階層問題は「なぜ α_G は小さいのか？」ではなく、「なぜ物質スケールはプランクスケールよりはるかに下にあるのか？」である—そして後者は重力についての問いではなく、物質スケールについての問いである。

本論文の貢献は、α_G を V35 と V52R の二重チャンネルおよび残差の枠組みの中で、極めて剛い記録媒体の変形効率として解釈することである。プランク剛性そのもの—したがって m_P を記録次元の固有剛性スケールとすること—の微視的導出は今後の課題として残す。

7.2 V53が主張すること・しないこと

主張すること ✓	主張しないこと ✗
α_G = (ℓ_P/ℓ_C)² は厳密な恒等式	プランク剛性の微視的起源
「空間剛性」としての解釈が可能	なぜ m ≪ m_P なのか
V35/V52Rの枠組みと整合	新しい動力学方程式

8. 結論

無次元重力結合定数

\[\alpha_G(m) = \frac{Gm^2}{\hbar c}\]

が厳密な表現

\[\alpha_G(m) = \left(\frac{m}{m_P}\right)^2 = \left(\frac{\ell_P}{\ell_C}\right)^2\]

を持つことを示し、後者を空間剛性の指標として解釈した：スケール ℓ_C のエネルギーが、プランクスケールで決まる固有剛性を持つ媒体を変形する効率である。

陽子の場合、この効率は 10⁻³⁹ 程度であり、観測される重力結合と一致する。YAGCの枠組みの中で、これは重力が極めて非効率な変換過程の小さな残り物であるという元来の直観を実現する—恣意的な小さなパラメータではなく。

                重力が弱いのは、空間が信じられないほど堅いからである。
            

V35の二重チャンネル記録次元と V52R の残差物理学と組み合わせると、V53は重力の弱さが情報構造的必然であることを示唆する：有限の記録次元に歴史を保存する宇宙は、非常に剛い空間を持たなければならず、したがって通常物質に対して非常に小さな重力結合を持たなければならない。

参考文献・関連論文

V0.1 — 創生的宇宙論：対話から生まれた重力の起源（2025年10月）
V35 — DCGH: Dual-Channel Gravitational Hypothesis（二重チャンネル重力仮説）
V52R — Quantum as Tolerance: 寛容原理と残差物理学
V52R Appendix — Gravitruct: 重力子構造仮説

概要