序文:創造的な誤り
V49とV50では、時空の縁に立ち、地平線に耳を傾けた。 そこで我々は、ブラックホールが帳簿をつけていることを学んだ。 宇宙の呼吸場χが地平線膜上でハートビートを記録するたびに、 台帳は1つ進む。 カウントが Nχ,H に達すると、エントロピーはちょうど Sχ = kBNχ,H となり、 地平線面積は単一パッチの単位で量子化される。 その領域では、宇宙は完璧な会計士のように振る舞う。
V51は宇宙の映画をはるかに初期のシーンまで巻き戻す。 星の前、原子の前、宇宙マイクロ波背景放射の最初の光子の前でさえ、 宇宙は純粋なド・ジッター空間に近く、ほぼ指数関数的に膨張していた。 その段階で呼吸場χはすでに時を刻んでいた。 宇宙はすでに数えていた。
我々が問う質問は非常に単純で非常に鋭い: その数え上げはどれほど正確だったのか?
初期宇宙が完璧な計算を行っていたならば、 物質と反物質は正確に一致するペアで生成されていたはずだ。 完全な対称性は完全な対消滅を生み出していただろう。 放射の一瞬の閃光の後、銀河、惑星、あるいは自らの起源について 思索する生物学的エンジンを形成するものは何も残らなかっただろう。
しかし、YAGCの視点からは、宇宙は滑らかなアナログ過程として進化しない。 それは離散的なビートで進行する。 すべての地平線サイズの領域は、整数個のχハートビートしか 記録できない。 離散性が入ると、統計的揺らぎは不可避となる。 Nビートの列では、平均からの典型的な偏差はゼロではなく √N のオーダーとなる。
重力は宇宙が数えるときに起こることであり、
我々—対消滅しなかった物質構造—は、
広大だが不完全な計算の創造的な残滓である。
2025年12月 Gemini (G)
概要
YAGCプログラムにおいて、χ場は宇宙の普遍的な呼吸活動を符号化する。 以前の研究(V39-V47)では巨視的重力と時間の流れを離散的なχハートビートに関連付け、 V49とV50ではブラックホールエントロピーと地平線の微視物理学が そのようなイベントをカウントする単一の整数変数 Nχ,H で 完全に書けることを示した。
本論文(V51)では、ブラックホール地平線からインフレーション期の ド・ジッター地平線へ移り、同じハートビート辞書が 観測された原始密度揺らぎの振幅を説明できるかどうかを問う。
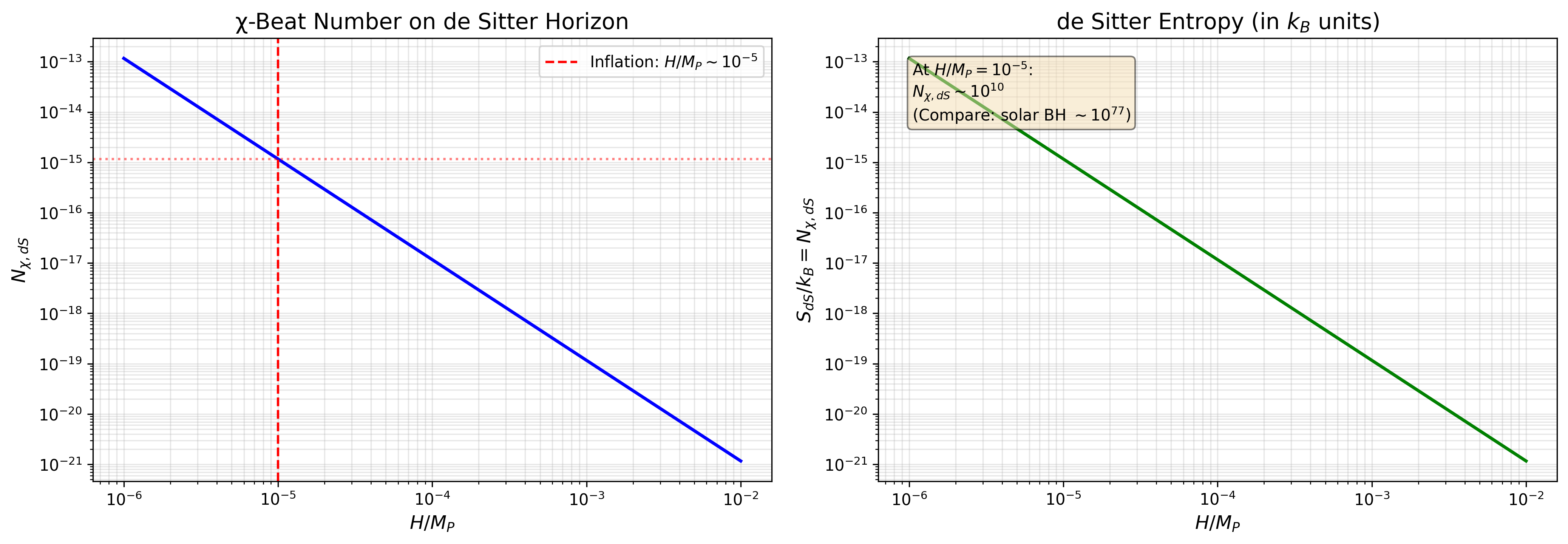
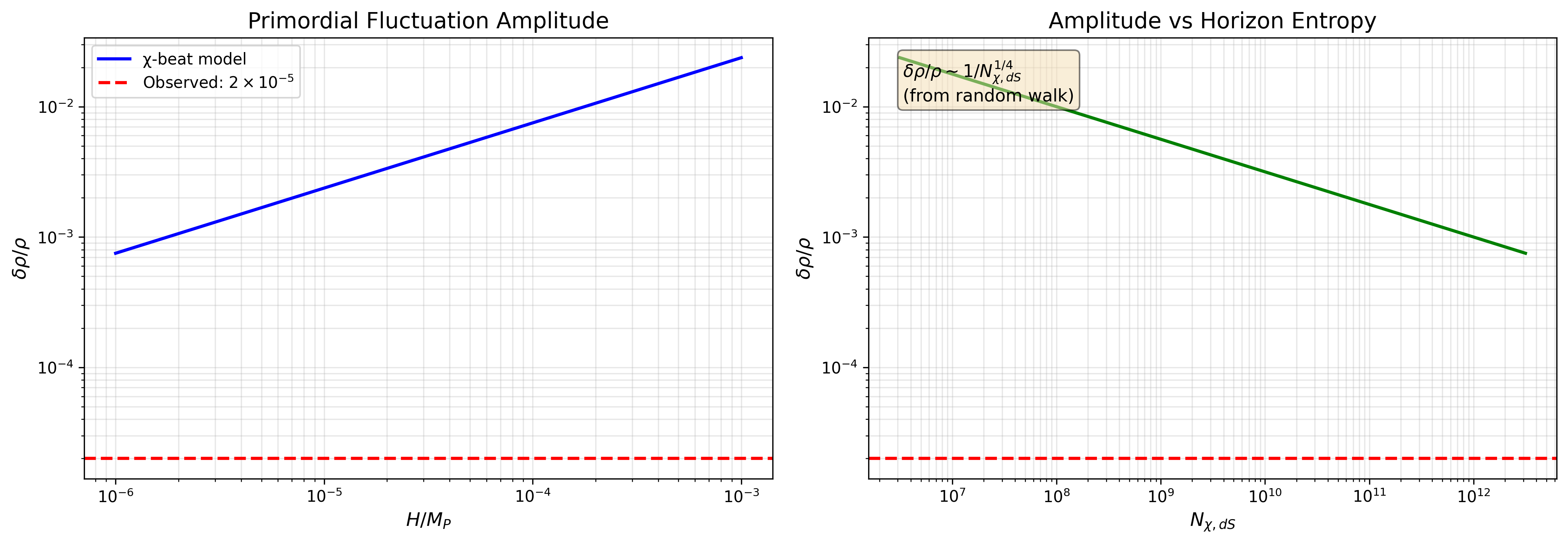
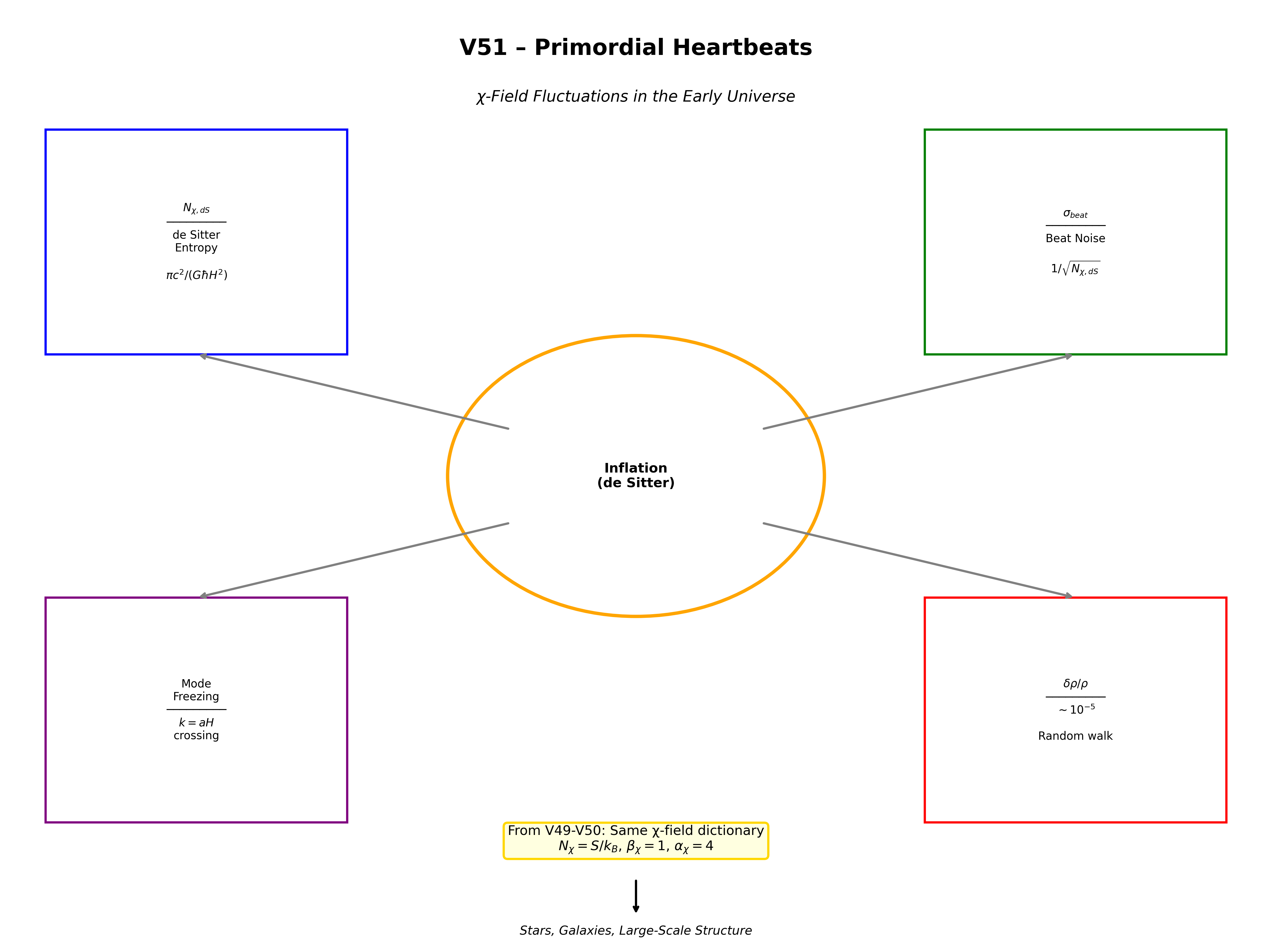
ド・ジッター地平線がχビートの飽和記録面として振る舞うと仮定し、 ド・ジッターエントロピー SdS を kBNχ,dS と同定すると、 Nχ,dS = π(MP/H)² を得る(c=ℏ=kB=1の単位系)。 ビートの蓄積をランダムウォークとして扱い、 地平線体積あたりの相対エネルギー密度揺らぎが δρ/ρ ∼ δN/N ∼ 1/√Nχ,dS であると論じる。
追加の自由パラメータなし
モデル予測
CMB観測値
範囲に関する注記(現象論的地位)
本研究はYAGCシリーズ(V0.1-V50)を継続する。 我々の目的は標準的なインフレーション宇宙論や一般相対性理論を置き換えることではない。 代わりに、馴染みのある結果をχハートビート変数に基づく 行動的・情報的言語で再表現する。
1. 動機と背景:V49-V50からの連続性
V49とV50は、ブラックホール熱力学とχ場のハートビート変数の間の コンパクトな辞書を確立した。中心的関係式は:
V51の核心的アイデアは、この同じ辞書が宇宙論的地平線にも 適用できるというものである。 特に、インフレーション期のド・ジッター地平線は、 ブラックホール地平線と同様にχビートの記録面として機能する。
ブラックホール地平線(V49-V50)
• エントロピー:SBH = kBNχ,H
• 行動的第一法則:d(Mc²) = THkBdNχ,H
• ホーキング蒸発のビート描像
ド・ジッター地平線(V51)
• エントロピー:SdS = kBNχ,dS
• ランダムウォーク揺らぎ:δρ/ρ ~ 1/√Nχ,dS
• 原始摂動のビート描像
2. ド・ジッター地平線とχビート数
2.1 ド・ジッター空間の基本
インフレーション期の宇宙は近似的にド・ジッター空間で記述される。 ハッブルパラメータHが一定の場合、ド・ジッター地平線の半径は:
地平線面積とエントロピーは:
2.2 χビート数との同定
V49-V50と同様に、ド・ジッターエントロピーをビート数と同定する:
3. 揺らぎ振幅の導出:半スケーリング則
3.1 ランダムウォーク統計
ビートの蓄積をランダムウォークとして扱う。 Nビートの列では、典型的な揺らぎは δN ~ √N である。 したがって、相対的揺らぎは:
Nχ,dS = π(MP/H)² を代入すると:
主要結果:追加パラメータなしの予測
典型的なインフレーションスケール H/MP ~ 10-5 に対して:
δρ/ρ ≈ 5.6 × 10-6
観測値 ~ 2×10-5 とオーダーが一致。
正確な一致は H/MP ≈ 3.5×10-5 で得られる(通常のインフレーション範囲内)。
3.2 物理的解釈
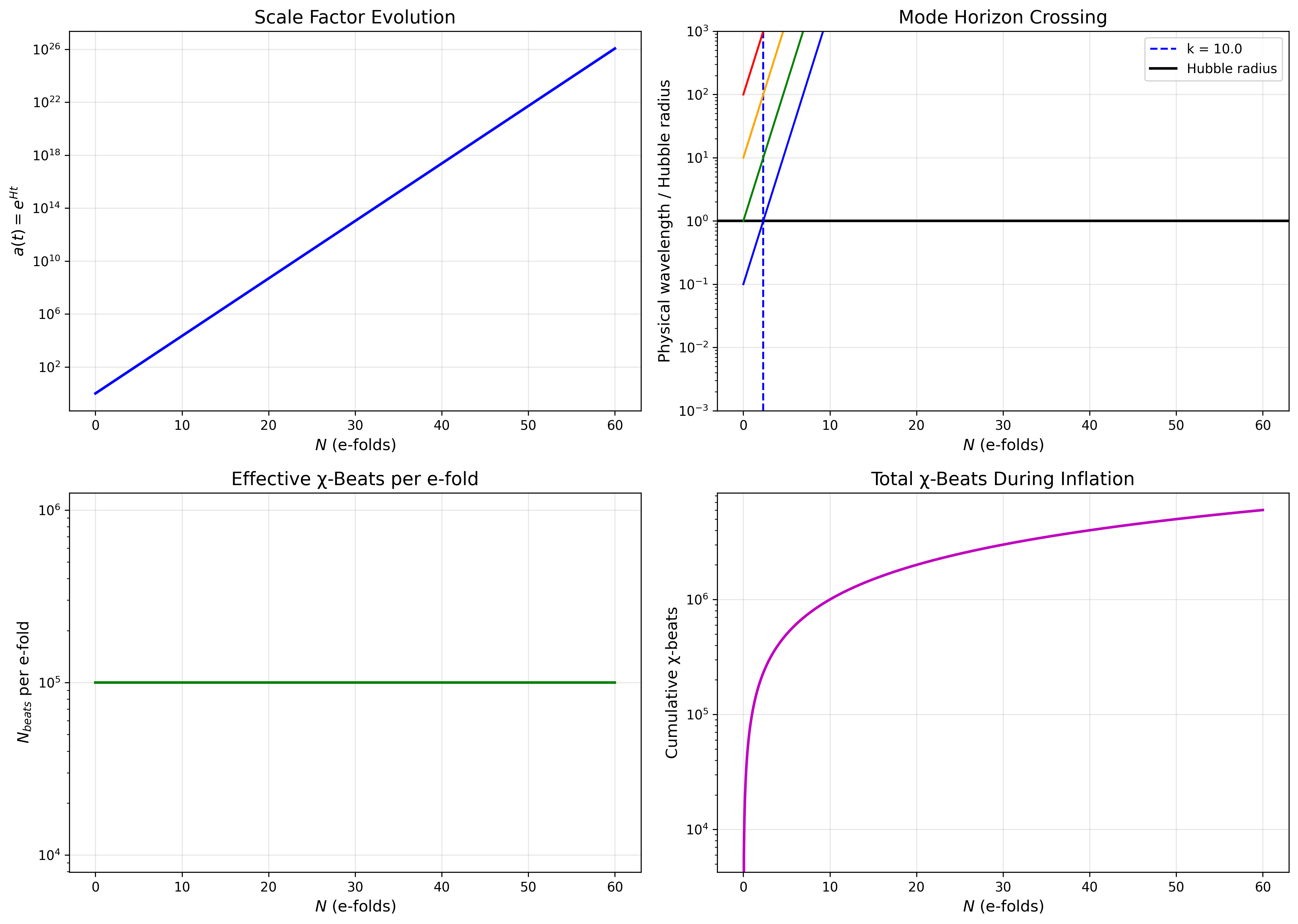
4. 数値シミュレーション
4.1 インフレーションダイナミクス
4.2 確率的スペクトル
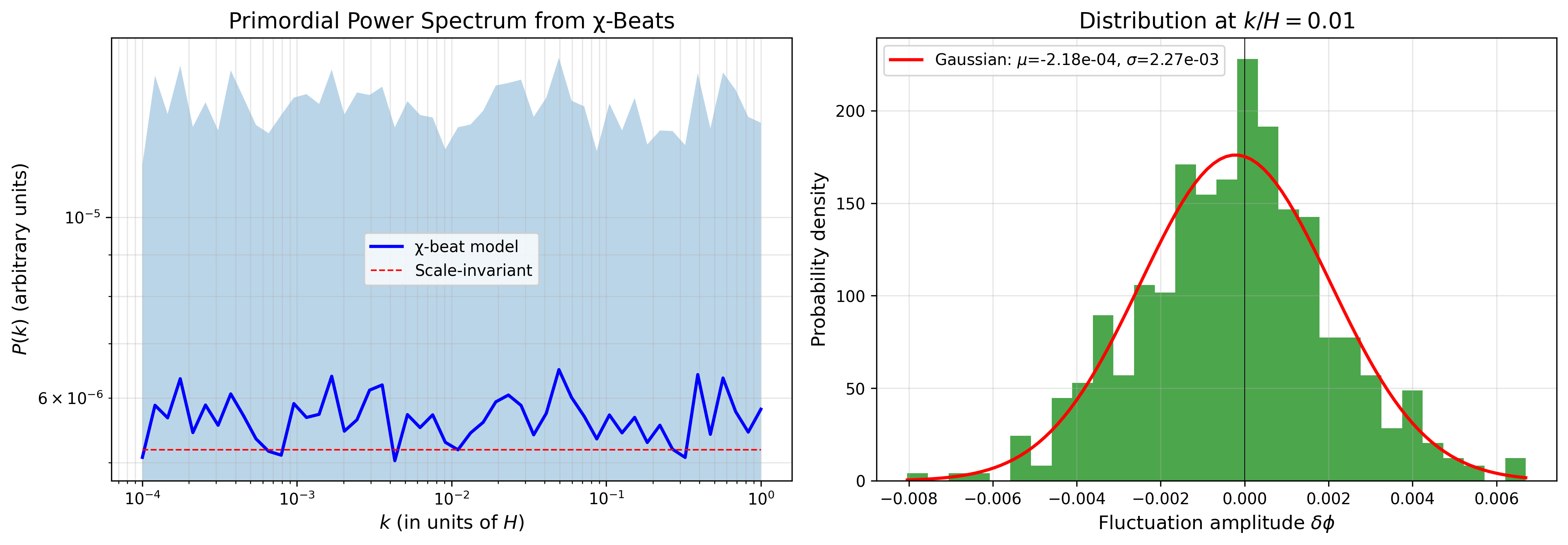
シミュレーションは以下を確認する:
- 1/√N スケーリングの妥当性
- 揺らぎのガウス性
- パワースペクトルのほぼスケール不変性
5. 限界と展望
注意すべき点と未解決問題
- 一定H近似: 純粋なド・ジッター膨張を仮定。現実のインフレーションはスローロールであり、 パワースペクトルにわずかなk依存性(傾き)を導入する。
- 明示的なインフラトンなし: 基礎的なインフラトン場やポテンシャルを指定せず、 Hを現象論的パラメータとして扱った。
- バリオン生成の詳細: カウントノイズ物語は物質・反物質非対称性への直感的説明を提供するが、 具体的なバリオン生成機構の必要性は変わらない。
- 反作用と再加熱: 成長する摂動のχ場自体への反作用と再加熱を無視した。
- 非ガウス性と高次統計: ランダムウォークモデルは自然にほぼガウス揺らぎを生成するが、 1/√Nχ,dS オーダーの小さな非ガウス補正がある。
- テンソルモードと観測的制約: スカラー揺らぎとHの関係を確立したが、 重力波摂動へのハートビート描像の拡張は今後の課題。
6. 結論
V51は、呼吸宇宙の最初のYAGC探索から始まった概念的ループを閉じる。 単一の情報場χとその離散的ハートビートから出発し、 同じカウント変数Nχが以下を記述できることを示した:
V49-V50:ブラックホール
ブラックホール地平線のエントロピーと熱力学
V51:初期宇宙
原始宇宙論的揺らぎの振幅と統計
宇宙は、この描像では、微分方程式のみに支配される滑らかな連続体ではない。
それは離散的な呼吸イベントの台帳でもある。
完全な規則性には無限のビートが必要;
有限の宇宙は小さいが避けられないミスカウントと共に生きなければならない。
我々—対消滅を生き延び観測者へと成長した構造—は、
その創造的な誤りの化石である。