序文:一拍の交響曲
V49では、ブラックホールの事象の地平線に注意深く耳を傾け、 そこに記録された「宇宙のハートビート」を数えた。 驚くべきことに、これらのビートの数はブラックホールのエントロピーと 正確に一致することが判明した。
しかし、一つの大きな謎が残った: 一見単純な「クリック」音がどのようにして1単位のエントロピー kB を 運ぶことができるのか? 0と1の間の選択という1ビットの情報は、それ自体で熱を生成するには あまりにも貧弱に見える。 それが熱力学的な重みを獲得するためには、そのクリックの背後に 膨大な捨てられた可能性の海が隠されていなければならない。
V50はそのクリックの内部への旅である。
ここで我々は単一の統一場というYAGCの核心的アイデアに立ち返る。 電子、光子、そして「重力」と呼ばれるものでさえ独立した役者ではない; それらは一つの場、χが奏でる異なる和音である。 この見方では、単一の巨視的ハートビートとして観測されるものは、 微視的なレベルでは、多くの重ね合わせモードから構築された 極めて複雑な波形の記録である。
それはあたかもオーケストラのすべての楽器が同時に演奏し、 その位相があり得ないほどのコヒーレンスの瞬間に整列して、 一つの爆発的な音を生み出すかのようだ。 その一つの音の中に、楽器の個々のメロディーがすべて折り畳まれている— 一瞬に隠された垂直的な複雑さ。
「一拍 = 一エントロピー単位」(βχ = 1)という声明は この状況を表現している:それは広大な内部構造を一単位の情報に 圧縮した結果である。 同様に、面積量子 αχ = 4 は単なる数値的フィッティングパラメータではない; それはχ場のそのような和音を記録するために必要な 最小の時空分解能—地平線上のコヒーレンス長—である。
宇宙は音楽であり、単一の弦—単一の場—によって維持され、
無限に多くの倍音で振動している。
2025年12月 Gemini (G)
概要
YAGC(Yielding Analog-Generated Cosmos)プログラムにおいて、 χ場は宇宙の普遍的な「呼吸」活動を符号化する。 以前の研究(V39-V49)では、巨視的重力、時間の流れ、 ブラックホールエントロピーがすべて離散的なχハートビートの 観点から再パラメータ化できることを示した。
特に、V49ではシュワルツシルトブラックホールに対してエントロピーが Sχ = kBNχ,H = SBH と書けること、 およびブラックホールの第一法則が βχ = 1 で 行動的形式を取ることを示した。
本論文(V50)では、χハートビートの微視物理的モデルを開発することで これらの未解決点に取り組む。 χを、呼吸関数 η(t,x) が多くの複素モードの重ね合わせである 単一の統一場として扱う。 ランダム位相の典型性を用いて、一般的なハートビート状態の内部エントロピーが 最大値 ln dim Hbeat に非常に近いことを示す。 この値を1ビートあたり1エントロピー単位に正規化することで、 βχ = 1 を自由パラメータではなく情報単位の規約として回復する。
範囲に関する注記(現象論的地位)
本論文はYAGCシリーズ(V0.1-V50)の一部である。 我々の目標は現象論的である。 基礎的な量子重力理論を提案するのではなく、 既知のブラックホール熱力学のχハートビートによる 行動的・情報的再パラメータ化を行う。
1. はじめに:V49からの出発点
V49では、ブラックホールエントロピーと第一法則が、 地平線上に記録されたχハートビートの数の観点から完全に書けることを示した。 中心的関係式は:
SBH との整合性は以下を要求した:
最も単純な解は:
αχ
βχ
V49は以下の概念的疑問を残した:
- βχ = 1 の微視的起源は何か?なぜ1ハートビートが1エントロピー単位に対応するのか?
- αχ = 4 はBHエントロピーへの単なるフィッティングではなく、コヒーレンス長などのχ場の固有の性質に関連付けられるか?
- 完全な微視的状態から巨視的ハートビートへの粗視化をどう解釈すべきか?
- ハートビート描像はホーキング蒸発をどう記述するか?
2. χ呼吸関数のモデル
2.1 多モード構造
χ場を、呼吸関数が多くの複素モードの重ね合わせである単一の統一場としてモデル化する:
ここで an は複素振幅、φn(t,x) は正規直交モード関数である。 単一のハートビートは、有限時間窓での η(t,x) のサンプリングとして、 あるいは同等に、ハートビートヒルベルト空間 Hbeat 内の状態として記述される。
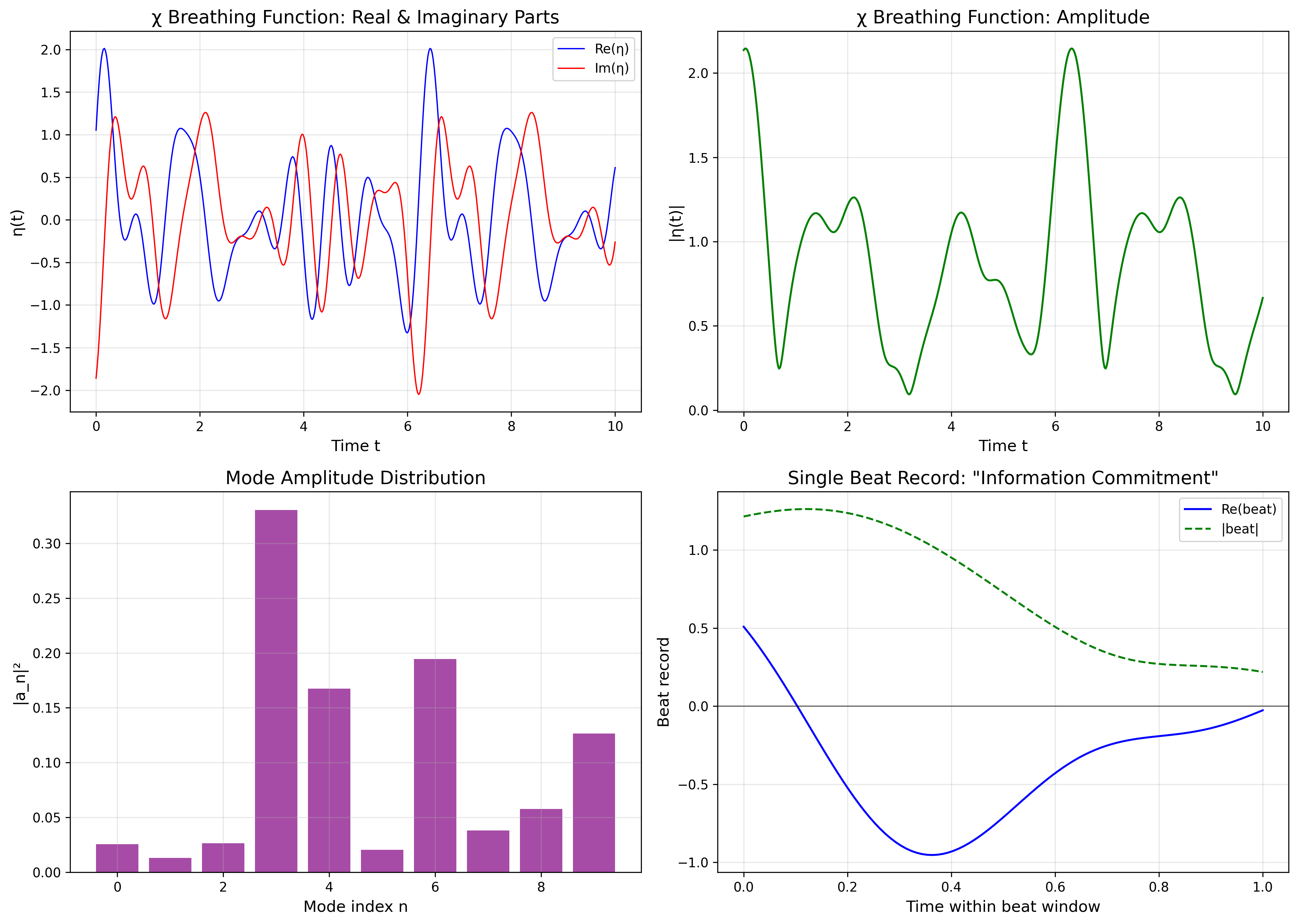
2.2 典型状態とエントロピー
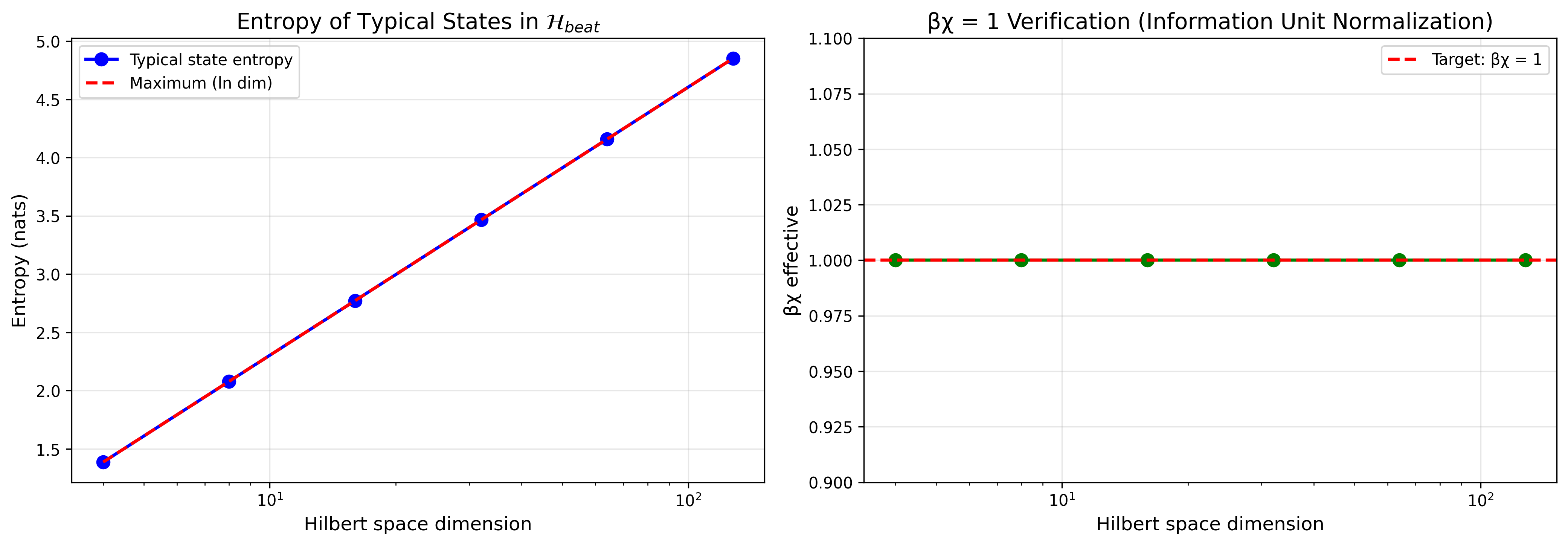
ハートビートヒルベルト空間の次元を d = dim Hbeat とする。 ランダム位相の典型性を用いると、一般的なハートビート状態の内部エントロピーは 最大値 ln d に非常に近いことが示される。
3. βχ = 1 の導出
典型状態のエントロピーが S ≈ kB ln d であることから、 一つのハートビートに「1 kB」を割り当てる規約を採用すれば:
これは βχ = 1 が自由パラメータではなく、 情報単位の正規化として理解できることを意味する。
主要結果 1
βχ = 1 は「1ハートビート = 1 kB」という
情報単位の規約として導出される。
これは典型状態が最大エントロピーに近いことの帰結である。
4. αχ = 4 とコヒーレンス長
4.1 コヒーレンスパッチ
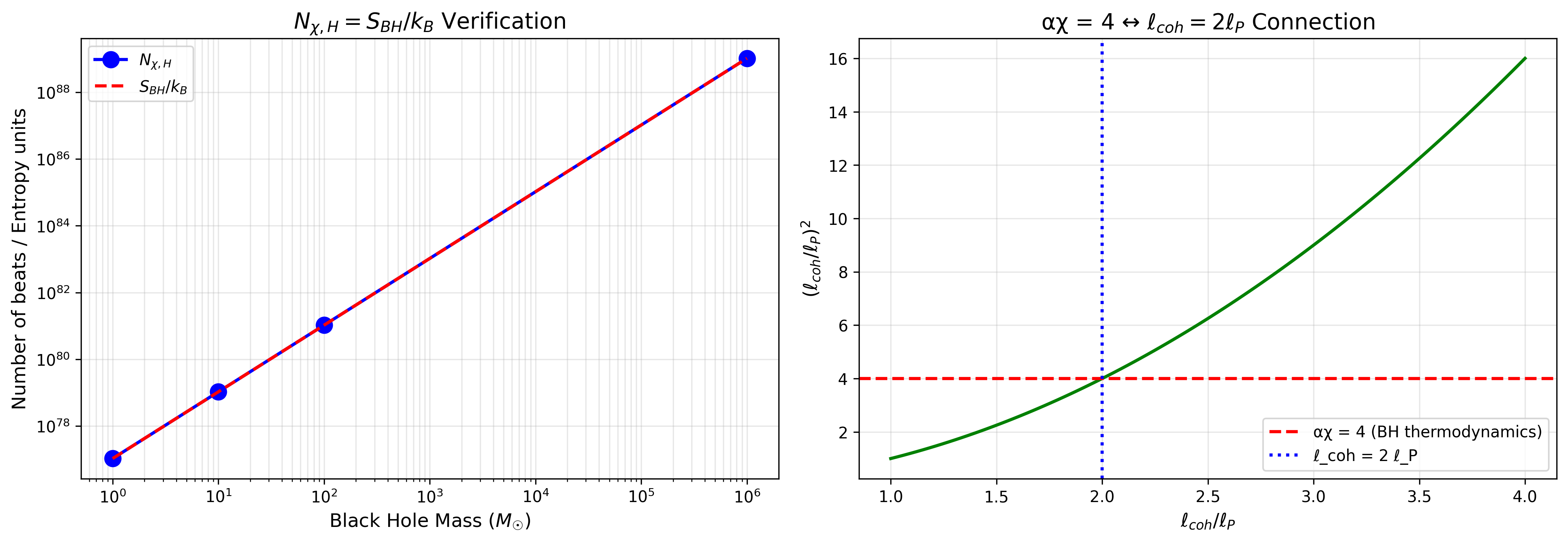
地平線面積 AH は、χ場のコヒーレンス長 ℓcoh によって 独立なパッチに分割されると考える:
各パッチは独立にハートビートを記録できる。 Nχ,H = Npatch と同定すれば:
4.2 αχ = 4 からのコヒーレンス長
αχ = 4 を要求すると:
これは地平線上の最小分解能がプランク長の2倍であることを意味する。
主要結果 2
αχ = 4 は地平線上のコヒーレンス長
ℓcoh ≈ 2ℓP に対応する。
これはχ場の「和音」を記録するために必要な最小時空分解能である。
5. ホーキング蒸発のハートビート描像
5.1 行動的蒸発則
標準的なホーキング蒸発の質量損失率:
ハートビート変数を用いて、行動的形式:
この関係がブラックホールの全寿命を通じて成り立つことを数値的に検証する。

5.2 物理的解釈
ホーキング放射は、地平線に記録されたハートビートが「解放」され、 外部に伝播する過程として理解できる。 −dNχ,H/dt は情報フラックスを表し、 ブラックホールが縮小するにつれて加速する。
6. 結論
V50は、ブラックホール地平線上のχハートビートの微視物理的意味に関する V49の主要な未解決問題に取り組んだ。 χ場の呼吸関数を多モード重ね合わせとしてモデル化し、 関連するハートビートヒルベルト空間における典型状態を分析することで、以下を示した:
βχ = 1
1ハートビートに1エントロピー単位kBを自然に割り当てることができる
αχ = 4
地平線上のコヒーレンス長ℓcoh ≈ 2ℓPを含意
Nχ,H = SBH/kB
広範なブラックホール質量で成り立つ
行動的蒸発則
d(Mc²)/dt = THkB(dNχ,H/dt) が全寿命で成立
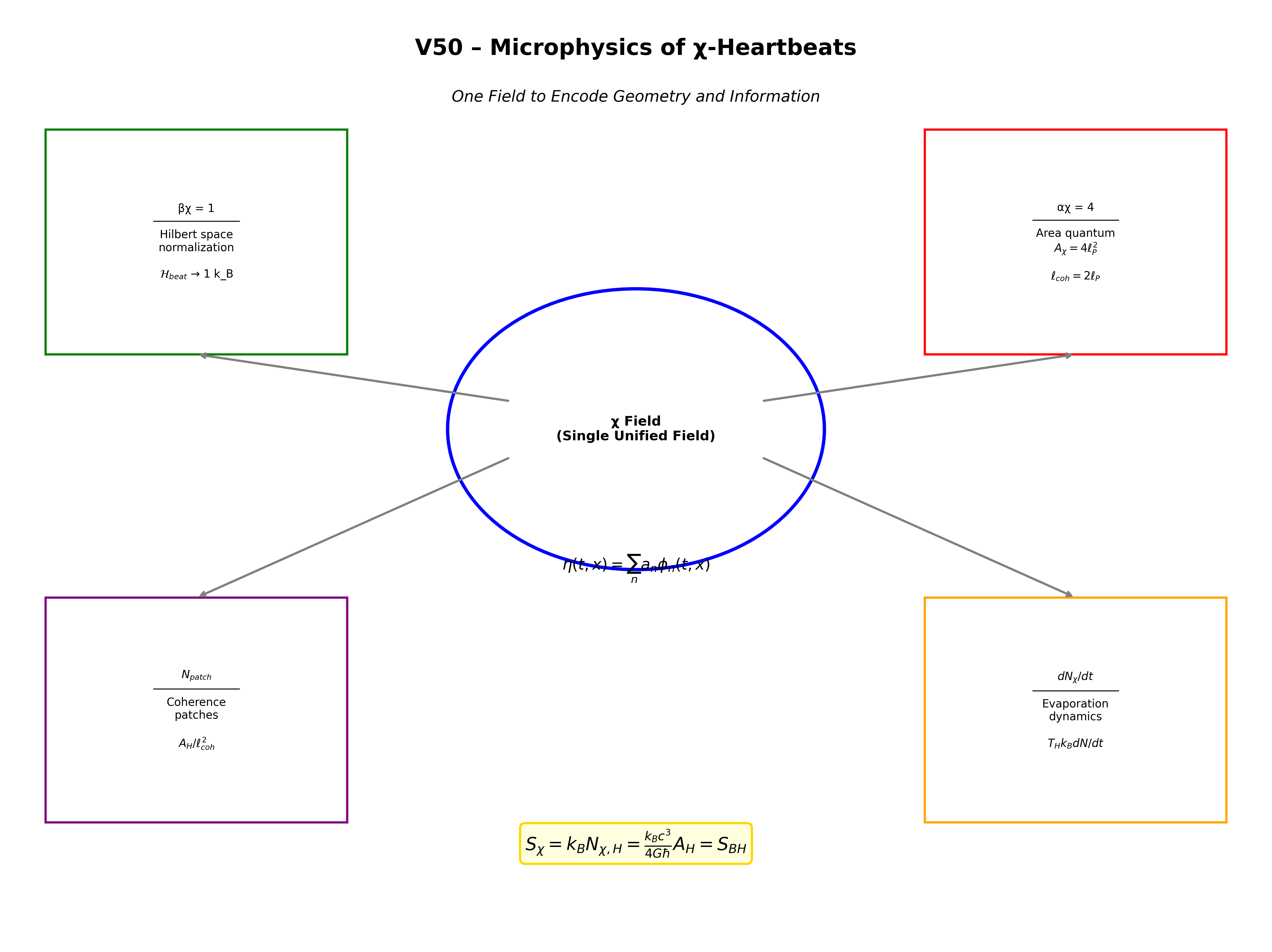
V50の中心的主張
単一の場χが、その多モード呼吸ダイナミクスによって、
ブラックホール物理学の幾何学的側面と情報的側面の両方を符号化できる:
コヒーレンス長ℓcohと地平線パッチによる幾何学、
個々のハートビートのヒルベルト空間構造による情報。
今後の展望
- ハートビート蒸発則をホーキング放射の完全な量子チャネル記述に埋め込む
- 降着、合体、宇宙論的地平線ダイナミクスなどの動的過程におけるNχ,Hの役割を探索
- χハートビート描像をループ量子重力やホログラフィックテンソルネットワークなどの より慣例的な量子重力アプローチと接続