概要
V41-V44シリーズでは、コミットメント場χと量子状態ψの間の呼吸型結合から 量子測定統計が創発する現象論的「χ場」モデルを開発した。 V45ではこの枠組みを二つの方向に拡張する。
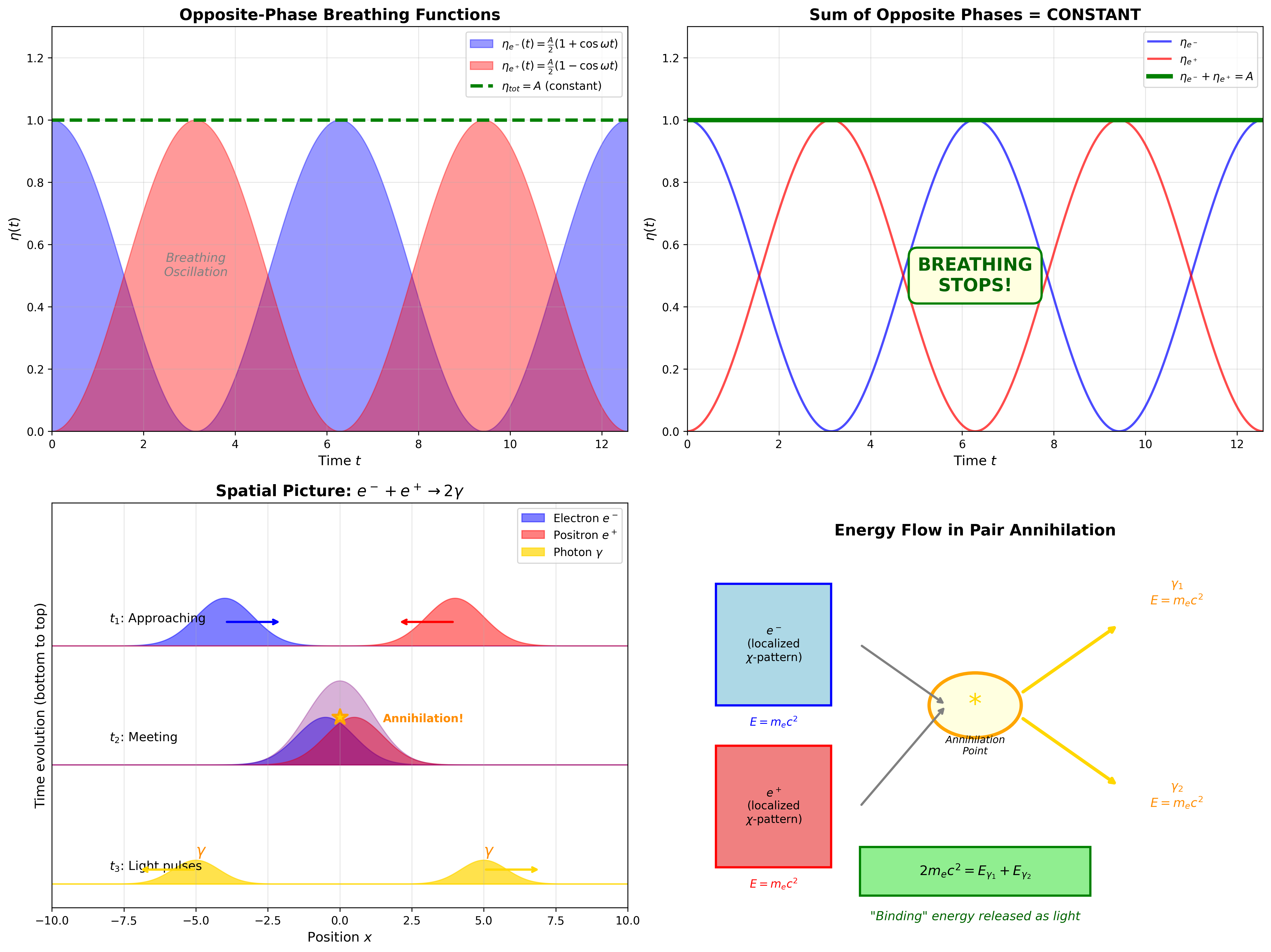
第一に、対消滅の呼吸場描像を提案する:電子e⁻と陽電子e⁺は χの逆位相呼吸パターンとして表現される。 これらのパターンが重なると、呼吸振幅の和はほぼ一定となり、 χの局所的呼吸は事実上「停止」し、蓄積されたパターンエネルギーは 伝播する光パルスへと転送される。
第二に、二重スリット形状におけるχ呼吸のコヒーレンス長 Lcoh(γ,D) の概念を導入する。 V43で開発した確率的ランジュバンダイナミクスを用いて、 有限減衰γとノイズ強度Dの下でボルン則相関 rBorn(L;γ,D) が 有効伝播距離Lと共にどのように減衰するかを計算する。 Lcoh ∝ 1/√D というスケーリングを数値的に示す。
1. はじめに
Vシリーズの過去の巻では、スカラー「コミットメント場」χが 宇宙が特定の結果にコミットした程度を符号化する情報中心の 宇宙論的枠組みを導入した。 V41では、χの適切なダイナミクスが単純な測定シナリオに対する ボルン則統計を再現できることを示した。 V42とV43はこの描像を有限減衰と確率的ノイズを含むように拡張し、 V44はこれらのダイナミクスを非負の「呼吸関数」に基づく 一般的な信号処理パラダイムとして再定式化した。
V45R3では、この作業仮説に動機付けられて以下を問う:
- 対消滅をχの逆位相呼吸パターンの相殺として、パターンエネルギーが光として放出されるものと見なせるか?
- 二重スリットにおける波動的から粒子的への振る舞いの移行を、χ呼吸のコヒーレンス長で定量化できるか?
2. 逆位相呼吸と対消滅
2.1 電子と陽電子の呼吸関数
呼吸パラダイムでは、各局在物質励起は非負の呼吸駆動によって 維持されるχのパターンとしてモデル化される。 対消滅に対して、電子と陽電子を等しい振幅と逆位相を持つ 2つの呼吸関数で表現する:
これらの和は時間に依存しない:
物理的解釈
電子と陽電子が分離している限り、逆位相呼吸パターンは局所的に作用し、 2つの異なるχ励起を維持する。 空間的波束が重なると、振動部分は相殺し、総呼吸は一定レベルに減少する。 その領域では呼吸駆動はもはや局在パターンを支えることができない。
2.2 空間的トイモデルと光パルス
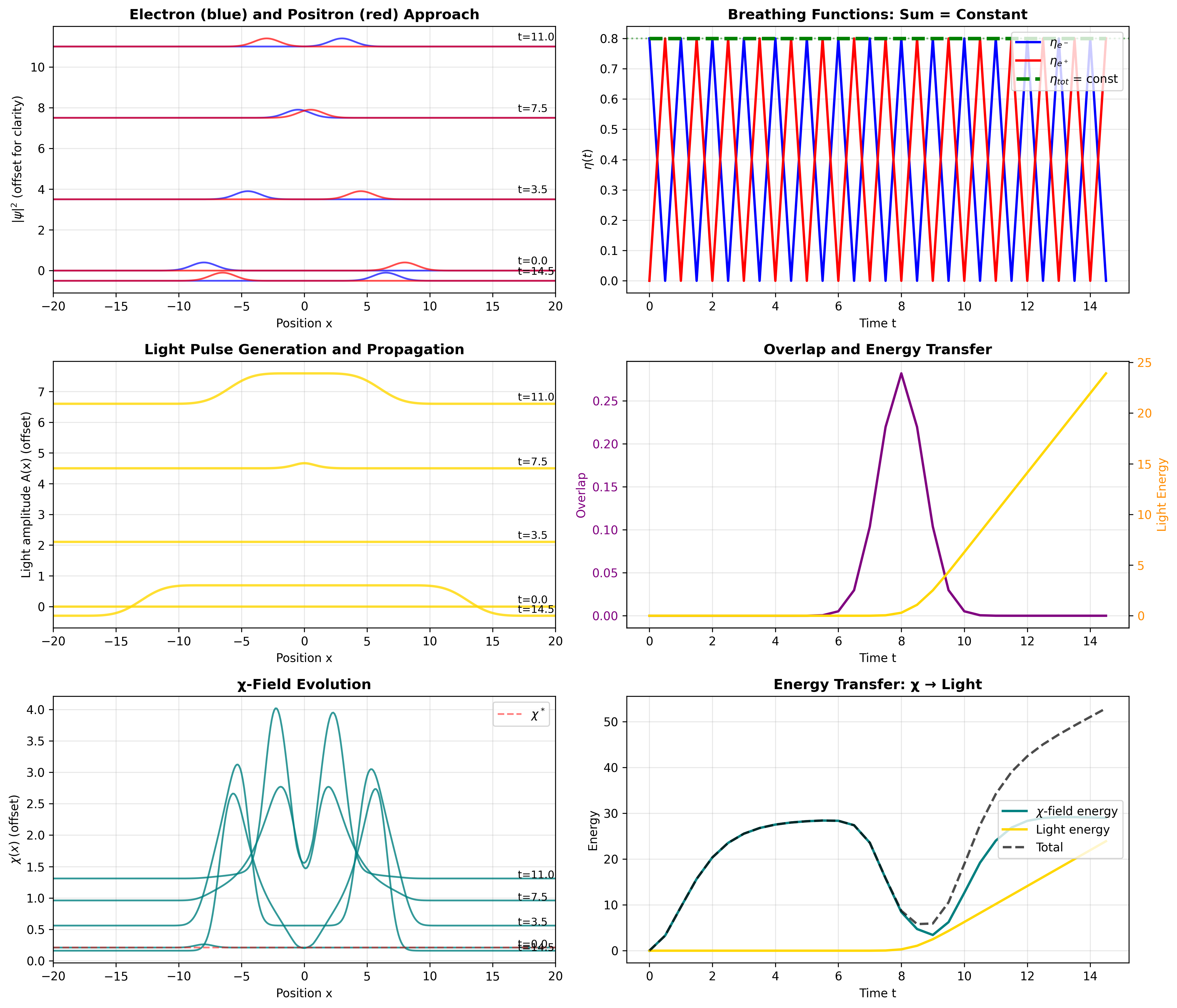
この描像をより具体的にするため、1次元トイモデルを導入する。 χ場を位置と時間の関数 χ(x,t) として記述し、 電子と陽電子の有効波動関数の絶対値の二乗 |ψe⁻(x,t)|² と |ψe⁺(x,t)|² に結合する。
χ場のパターンエネルギーの損失に比例するソース項によって駆動される 光場A(x,t)の単純な波動方程式を補完する:
ここで Sγ は逆位相呼吸パターンが相殺する期間にのみ非ゼロとなる。 これにより消滅領域から伝播する光パルスが生成される。
2.3 エネルギー論と限界
このトイモデルの目的のため、単純なエネルギー汎関数を定義する:
総エネルギー Etot(t) = Eχ(t) + EA(t) の近似的保存を監視する。 数値実験では、呼吸相殺条件が満たされると Eχ は減少し、 EA は対応する量だけ増加する。
限界の明示
このトイモデルが行わないことを強調することが重要である。 正しい光子スペクトル、断面積、スピン選択則、その他の量子電磁力学の予測を 再現しようとはしていない。 モデルは、呼吸パラダイム内に「対消滅は閉じ込められた呼吸パターンの破壊と そのエネルギーの伝播波への放出に対応する」という一貫した構造的描像が 存在することを示すのみである。
3. 二重スリットにおけるχ呼吸
3.1 ランジュバンダイナミクス(V43の復習)
V43では、与えられた検出器位置でのχ場を、以下の形式の ランジュバン方程式に従う確率変数としてモデル化した:
ここで γ は緩和率、χ* は参照レベル、η(t) は(非負の)呼吸駆動、 ξ(t) は ⟨ξ(t)ξ(t')⟩ = δ(t−t') を持つガウス白色ノイズである。 パラメータDは確率的揺らぎの強度を制御する。
3.2 ボルン相関とコヒーレンス長
観測されたパターンが理想的な干渉像とどれだけ一致するかを定量化するため、 ボルン相関を計算する:
弱い減衰とノイズ、短い有効距離Lでは、χのダイナミクスは 構造化された駆動 η(t)|ψ|² に支配され、rBorn ≈ 1 となる。 Lが増加すると、確率的揺らぎが蓄積し rBorn は減衰し、 干渉の漸進的な喪失を示す。
コヒーレンス長 Lcoh(γ,D) を、閾値 rth を選び以下で定義する:
本巻では保守的な基準として rth = 0.5 を採用する。
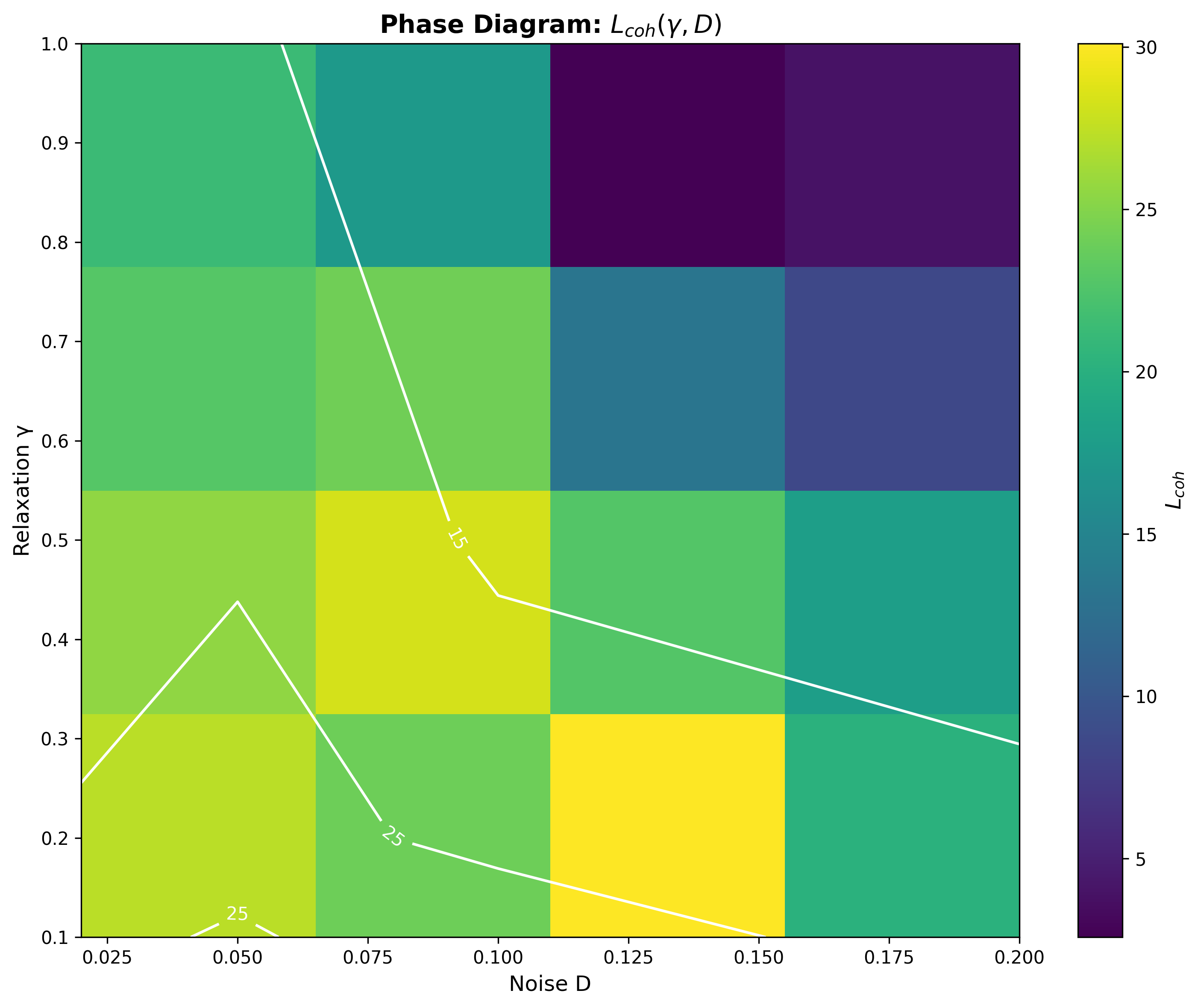
4. Lcohの数値結果
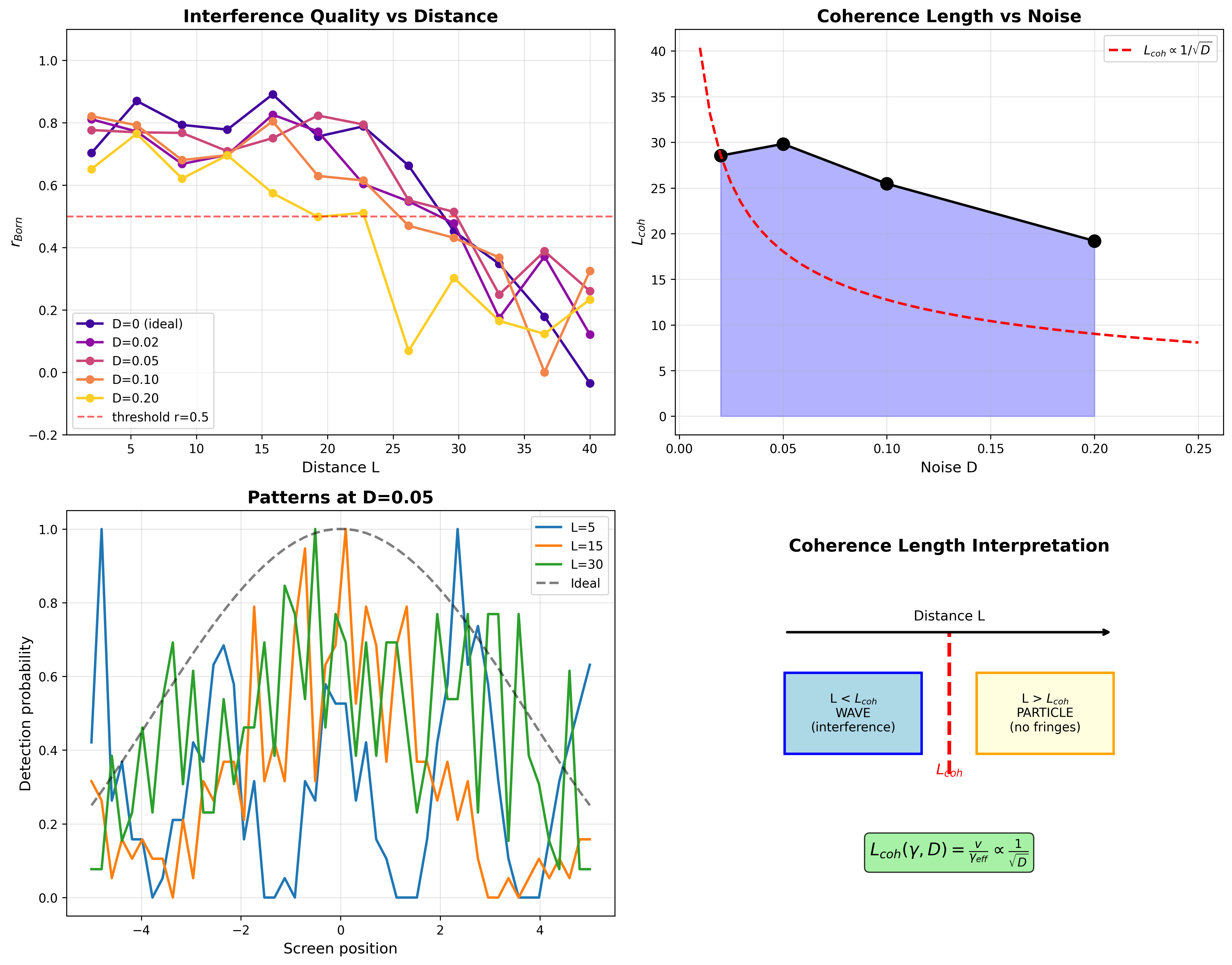
探索した限られたDの範囲で、以下と整合する近似的に線形な依存性を見出す:
これはこのトイモデルにおける数値的傾向として読むべきであり、 普遍的な自然法則としてではない。
5. 考察
5.1 閉じ込められた呼吸としての物質
対消滅トイモデルは、物質がχ場における閉じ込められた呼吸のパターンに 対応するというアイデアを実現する。 単純なエネルギー汎関数の限界内で、総エネルギーは近似的に保存される。
5.2 有限コヒーレンス長としての波動・粒子二重性
二重スリット形状では、同じχ呼吸ダイナミクスが自然に コヒーレンス長 Lcoh(γ,D) を導く。 佐藤の当初の直感—「崩壊距離は波が波であり続けられる距離である」—が ここに定量化される。
5.3 V43およびV44との関係
本巻はV43およびV44との概念的三位一体を完成させる:
V43
呼吸 vs ノイズ競合からのボルン則統計
V44
BDIは時系列における呼吸優位性を測定
V45R3
Lcohは呼吸の空間的コヒーレンスを測定
統一された描像
物質は閉じ込められた呼吸、
光は解放された呼吸、
波動・粒子二重性はノイズ環境における呼吸パターンの有限コヒーレンス長を反映する。
5.4 限界と未解決問題
モデルの限界
- 対消滅モデルはスピン、電荷、量子数を無視している
- 二重スリットシミュレーションは有効距離 L = veffT を使用
- スケーリング Lcoh ∝ 1/√D は限られたパラメータ範囲でのみ観測された
これらの注意点にもかかわらず、モデルは単一の呼吸場パラダイム内で 物質から光への変換、干渉の喪失、ボルン則を結びつける 首尾一貫した物語を構築することが可能であることを示している。
6. 結論と展望
V45R3は呼吸パラダイムをどこまで押し進められるかを探求する。 物質は閉じ込められた呼吸、光は解放された呼吸、 波動・粒子二重性はノイズ環境における呼吸パターンの有限コヒーレンス長を 反映するという統一された描像を得る。
今後の研究では以下に取り組む:
- 現実的な運動学の組み込み
- Lcohの重力ポテンシャルへの結合(V35、V39)
- トイモデルと実験データの対照