V44R: 呼吸パラダイム

概要

本研究では「呼吸分解」—非負の周期関数η(t) = (1 + cos ωt)/2を基底とした信号分解法—を提案する。一見ランダムに見える揺らぎf(t)を複数の呼吸モードの和 Ση_k(t) とノイズに分解し、「呼吸優位指数」(BDI: Breathing Dominance Index)により決定論的構造の寄与を定量化する。 BDI ≥ 0.95のとき、揺らぎの大部分は隠れた周期構造で説明される。 V43の量子ハートビートモデルとの統合により、ボルン則相関rとBDIが共に「決定論的呼吸 vs. 確率的ノイズ」の比率を測定することを示し、 V41-V44シリーズの理論的一貫性を確立する。

1. はじめに

物理系における「揺らぎ」は、しばしばランダムなノイズとして扱われる。しかし、V43の量子ハートビートモデルでは、χ場の時間発展において「呼吸」と呼ばれる周期的変調が本質的な役割を果たすことが示された。

本研究（V44R）では、この洞察を一般化し、任意の時系列信号に適用可能な「呼吸パラダイム」を提案する。核心的なアイデアは以下である：

呼吸パラダイムの核心

一見ランダムに見える揺らぎは、実際には複数の非負周期モードの重ね合わせと真のノイズの和として理解できる。各モードは「弱まることはあっても決して逆転しない」という物理的制約を満たす。

これは「宇宙は止まれない」というYAGCの基本原理と整合する：情報の流れは一時的に減少しても、決して負になることはない。

2. 関連研究と方法論的文脈

呼吸分解は、いくつかの確立された手法と特徴を共有しつつ、重要な構造的制約において異なる。主要な3つの枠組みとの関係を整理する。

2.1 フーリエ解析との関係

標準的なフーリエ分解は信号を以下のように表現する：

f(t) = Σ_k (a_k cos ω_kt + b_k sin ω_kt)

係数(a_k, b_k)は正負の任意の実数値を取りうる。呼吸分解は表面的には類似—どちらも振動モードの線形重ね合わせ—だが、 2つの本質的な点で異なる：

非負性制約：各呼吸モード η_k(t) ≥ 0（すべてのtで）。フーリエモードは正負を自由に振動するが、呼吸モードはそうではない。
シフトコサインテンプレート：形式 η_k(t) = A_k(1 + cos(ω_kt + φ_k))/2 は組み込みのDCオフセットを持ち、モードは[0, A_k]の間で振動する。

2.2 経験的モード分解（EMD）との関係

経験的モード分解とHilbert-Huang変換は、純粋にデータ駆動のシフティングプロセスにより信号を固有モード関数（IMF）に分解する。対照的に、呼吸パラダイムはモデルベースである：各モードが特定の関数形式 (1 + cos(ω_kt + φ_k))/2 を持つと仮定する。

2.3 非負行列分解（NMF）との関係

非負行列分解はデータ行列を V ≈ WH（W, H ≥ 0）と分解する。呼吸分解はこの構造化された変種と見なせる：「辞書」{h_k(t)}が自由に学習されるのではなく、呼吸テンプレートに固定される。

2.4 手法の比較

手法	非負性	パラメトリック	物理的解釈
フーリエ	いいえ	はい	周波数成分
EMD / HHT	いいえ	いいえ	IMF（データ駆動）
NMF	はい	いいえ	学習された成分
呼吸分解	はい	はい	(A_k, ω_k, φ_k)

呼吸パラダイムは独自のセルを占める：非負、パラメトリック、かつVシリーズの情報ダイナミクスの観点から直接解釈可能。

3. 呼吸分解の理論

3.1 なぜ η(t) = (1 + cos ωt)/2 なのか？

特定のテンプレート (1 + cos ωt)/2 を選ぶ理由について、 2つの相補的な正当化を提供する。

最小性の議論

「標準的な非負振動」に対する以下の要件を考える：

単一の基本周波数ωによる周期性
非負性：η(t) ≥ 0（すべてのtで）
滑らかさ：η ∈ C^∞（無限回微分可能）
正規化された平均：⟨η⟩_T = 1/2
対称性：各半周期で同じ形状

最小のスペクトル成分（単一の調和波）で(1)-(5)を満たす唯一のC^∞解は：

η(t) = (1 + cos ωt) / 2

3.2 物理的解釈（YAGCコンテキスト）

Vシリーズの枠組みでは、η(t)は情報がχ場に流入する速度を変調する。 V43のランジュバン方程式における駆動項は η(t)|ψ|² であり、|ψ|² ≥ 0 は既に保証されている。

もしη(t)が負になることを許せば、駆動はχに情報を注入するのではなく抽出することになる。情報保存の観点（YAGCの核心的仮説）から、このような「逆呼吸」は禁止される：宇宙は吸入を一時停止できるが、負に吸入することはできない。

「宇宙は止まれない」

任意の瞬間において、総呼吸振幅 Σ_kη_k(t) は小さくなりうるが、決して負にならない。これにより情報の流れは常に前方向に向けられることが保証される。

3.3 呼吸優位指数（BDI）

呼吸優位指数は、分散の比として定義される：

BDI = Var(Ση_k) / Var(f)

BDIは回帰における決定係数R²に類似しており、観測された揺らぎのうち呼吸成分で説明される割合を測定する。BDI ≥ 0.95のとき、信号は「呼吸優位」と分類される。

3.4 モード数の選択

BDIはR²に類似しているため、モード数を増やすと一般にBDIは増加する。これは過適合のリスクを生む。これを防ぐため、最小モード基準を採用する：

BDI(N) ≥ BDI_crit または ΔBDI < ε を満たす最小のNを選択

本論文の合成テストでは、BDI_crit = 0.95、ε = 0.01を使用する。ノイズD ≤ 0.05の5モード真値に対して、N = 5が最小十分集合として回復される。

4. 検証結果

4.1 パラダイムのデモンストレーション

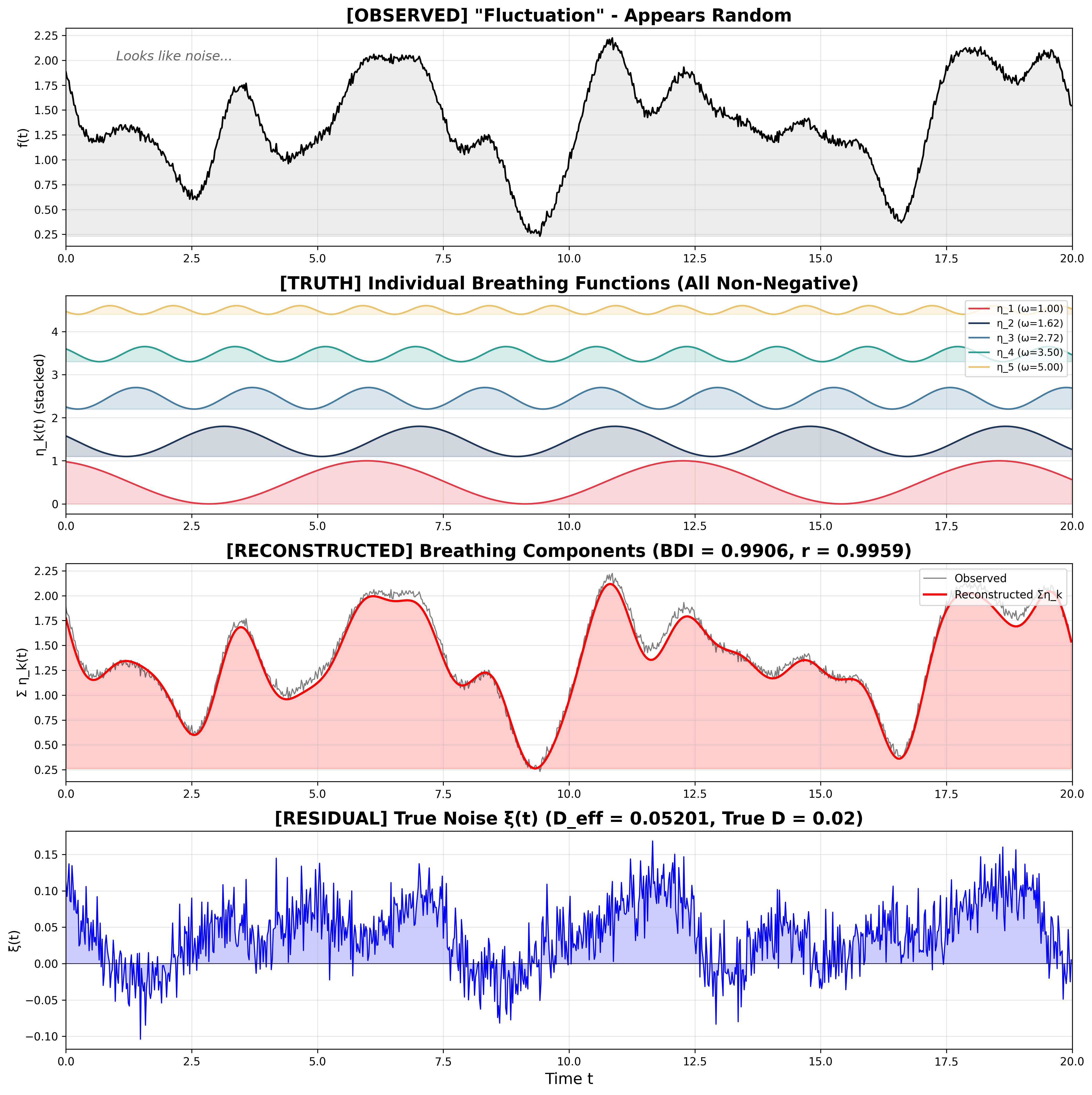
**図1: 呼吸パラダイムのデモンストレーション。** 上段：一見ランダムに見える「揺らぎ」f(t)。第2段：真の個別呼吸関数（すべて非負）。第3段：再構成された呼吸成分（BDI = 0.9906, r = 0.9959）。下段：真のノイズξ(t)（残差）。ノイズのように見える信号が、実際には複数の非負周期モードの重ね合わせであることを示している。

4.2 ノイズ強度に対する検証

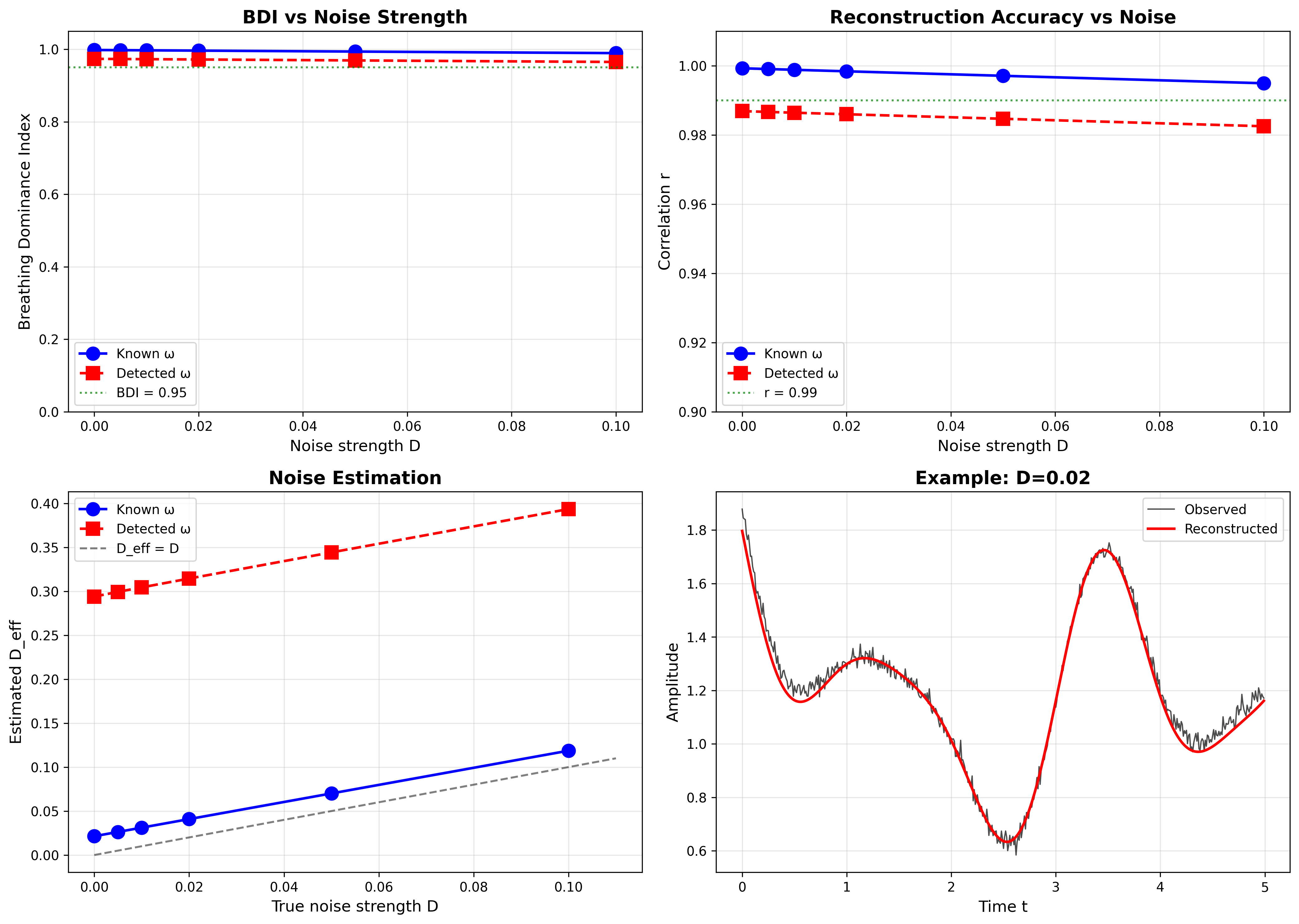
4.3 V43-V44概念統合

V43-V44概念統合図 — **図3: V43-V44概念統合。** V43（χ場ハートビート）とV44（呼吸パラダイム）は共通の呼吸関数η(t) = (1 + cos ωt)/2を基盤として共有する。V43は呼吸を使ってχを駆動し量子測定を行い、 V44は呼吸を基底として揺らぎを分解する。両者とも「決定論的呼吸 vs. 確率的ノイズ」の比率を測定する。

5. V43-V44統合

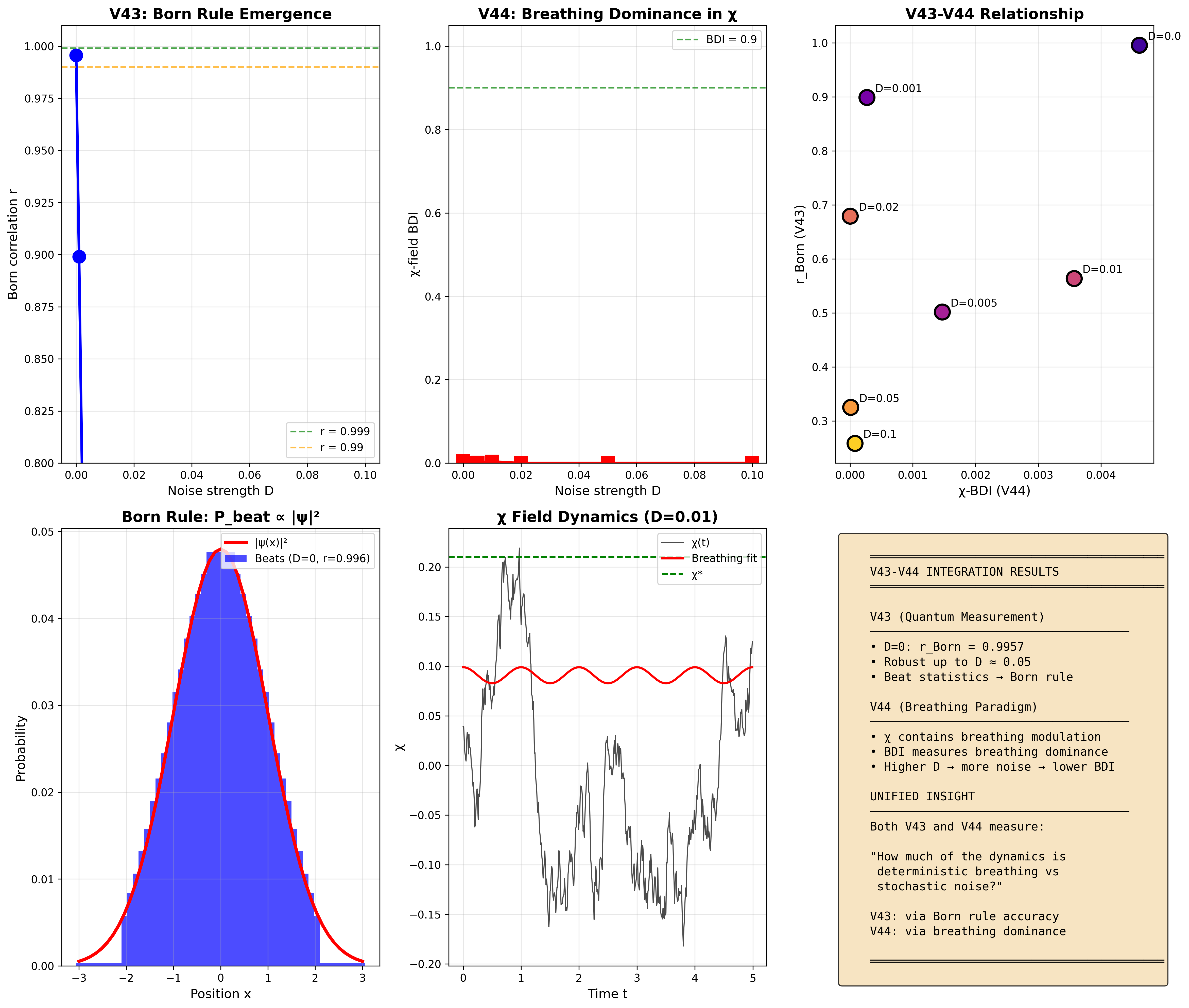
**図4: V43-V44統合結果。** 左上：V43ボルン則創発（D=0でr ≈ 0.999）。中央上：V44呼吸優位（χ場のBDI）。右上：V43-V44関係（r_Born vs BDI、ノイズDでパラメータ化）。左下：ボルン則検証（P_beat ∝ |ψ|²）。中央下：χ場ダイナミクス（D=0.01）。右下：統合結果サマリー。

統合された洞察

V43（量子測定）

D=0: r_Born = 0.9957
D = 0.05まで頑健
ビート統計 → ボルン則

V44（呼吸パラダイム）

χは呼吸変調を含む
BDIは呼吸優位性を測定
高D → より多いノイズ → 低BDI

V43とV44は共に測定する：
「ダイナミクスのどれだけが決定論的呼吸で、どれだけが確率的ノイズか？」

5.1 相関の物理的意味

指標	高い値	低い値
r（V43）	呼吸優位（決定論的構造）	ノイズ優位（ランダム揺らぎ）
BDI（V44）	呼吸優位（決定論的構造）	ノイズ優位（ランダム揺らぎ）

高r・高BDI → 呼吸優位（決定論的構造）
低r・低BDI → ノイズ優位（ランダム揺らぎ）

6. 結論

V44Rでは「呼吸パラダイム」—非負周期関数を基底とした信号分解法—を提案し、 V43との理論的統合を達成した。主要な成果は以下の通りである：

呼吸分解の数学的枠組みを確立（フーリエ、EMD、NMFとの比較を含む）
η(t) = (1 + cos ωt)/2 の選択を最小性と物理的考察から正当化
呼吸優位指数（BDI）による定量的評価法を導入
合成データでBDI ≥ 0.95、相関r ≥ 0.99を達成
V43のボルン則相関rとV44のBDIが共に「呼吸 vs. ノイズ」比を測定することを示す
V41-V42-V43-V44シリーズの理論的一貫性を確立

呼吸パラダイムは、「宇宙は止まれない」というYAGCの基本原理を、信号解析の具体的手法として実現したものである。一見ランダムな揺らぎの中に、決定論的な周期構造が隠れている— この洞察は、量子測定（V43）から信号処理（V44）まで、幅広い応用可能性を持つ。

目次

概要