概要
V41で確立された量子ハートビートモデルに、環境バス結合に由来するランジュバンノイズを導入し、 ボルン則相関のパラメータ依存性を数値的に調査した。 決定論的極限(D=0)では r ≃ 0.9999 を達成し、V41の結果と整合する。 ノイズ強度Dの増加に伴い相関が減少することを確認した。 また、Dの関数としてのビートカウントに非単調な振る舞いを観測し、 これをノイズ支援活性化とノイズ誘起抑制の競合として解釈する。 本研究により、(τ, D)位相図上での「良い測定窓」と「悪い測定窓」のコントラストの可視化が可能となり、 V41からV42を経てV43に至る理論的進展を完成させた。
1. はじめに
V41では、量子測定に対するボルン則 P(x) ∝ |ψ(x)|² がχ場のダイナミクスから創発することを示した。 V42では、有限減衰率γの効果を検討し、過減衰極限からの逸脱が飽和効果を生むことを明らかにした。
本研究(V43R)では、環境バスへの結合に起因する確率的揺らぎを導入する。 揺動散逸定理(FDT)によれば、減衰γとノイズ強度Dは本質的に結びついており、 有限温度環境では両者が同時に現れる。 これらの条件下で、(τ, D)パラメータ空間全体にわたってボルン則相関がどのように修正されるかを系統的に調査する。
2. 確率的ハートビートモデル
2.1 ランジュバン方程式
V41の過減衰ダイナミクスに確率項を加えたランジュバン方程式を考える:
ここで、γ = 1/τ は減衰率、Dはノイズ強度、ξ(t)は白色ガウスノイズである。 呼吸変調項 breathing(t) = (1 + cos ωt)/2 は二モード干渉から生じる。
2.2 測定モデル
各空間位置xにおいて、χ(x, t)は時間的に独立に発展し、 χ*を下から横切るたびに「ビート」としてカウントされる。 長時間シミュレーション後、ビートカウント分布 beat_counts(x) と |ψ(x)|² の間の ピアソン相関rをボルン則の指標として用いる。
2.3 パラメータ設定
| パラメータ | 記号 | 値 | 意味 |
|---|---|---|---|
| 閾値 | χ* | 0.21 | ビート生成閾値 |
| 緩和時間 | τ | 2.0 -- 20.0 | 減衰時定数 |
| 結合強度 | η | 0.8 | |ψ|²結合係数 |
| ノイズ強度 | D | 0 -- 0.05 | ランジュバンノイズ |
| 時間刻み | dt | 0.01 | 数値積分ステップ |
3. シミュレーション結果
3.1 決定論的 vs. 確率的ダイナミクス
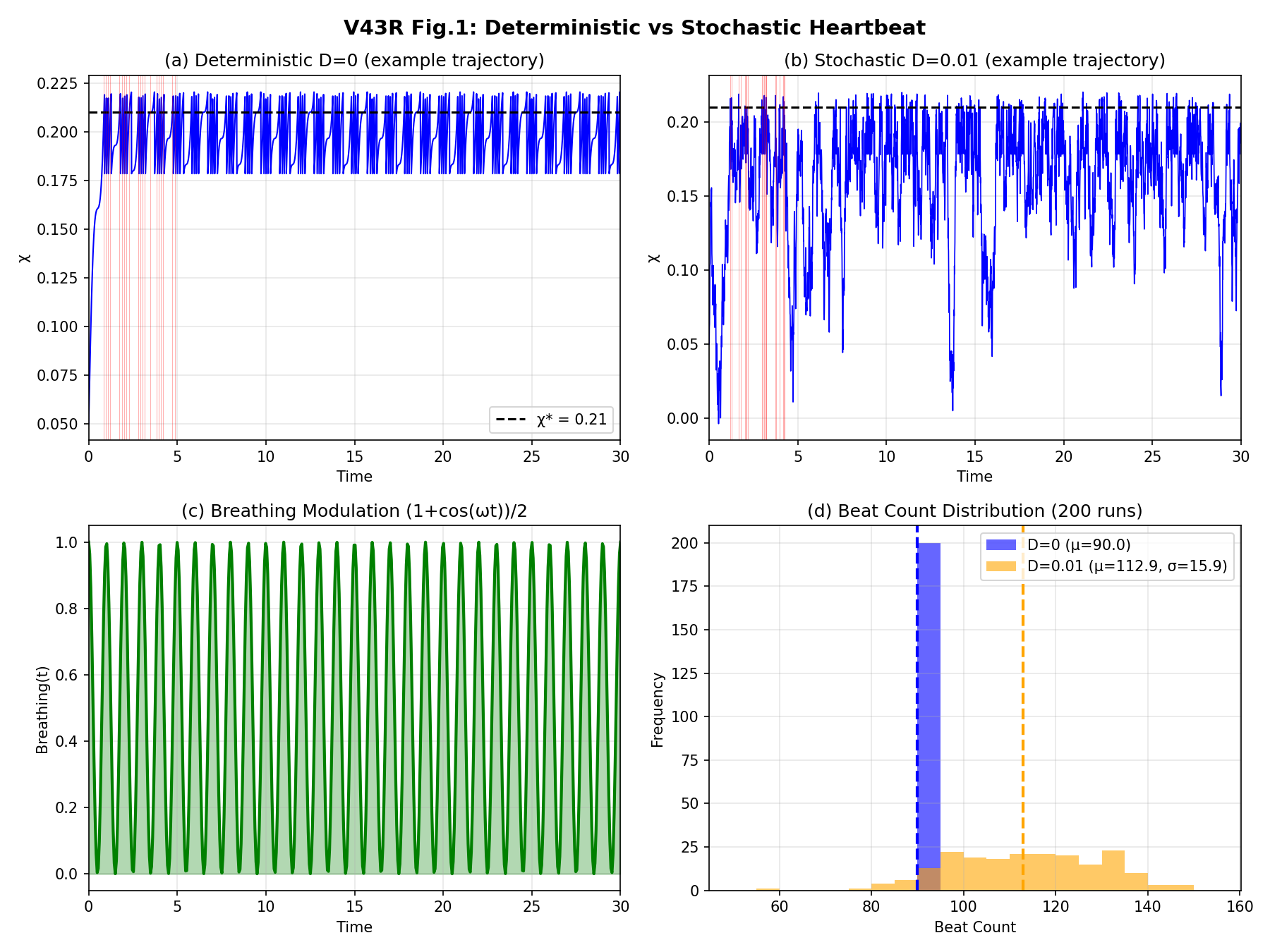
3.2 ノイズ強度の効果:非単調な振る舞い
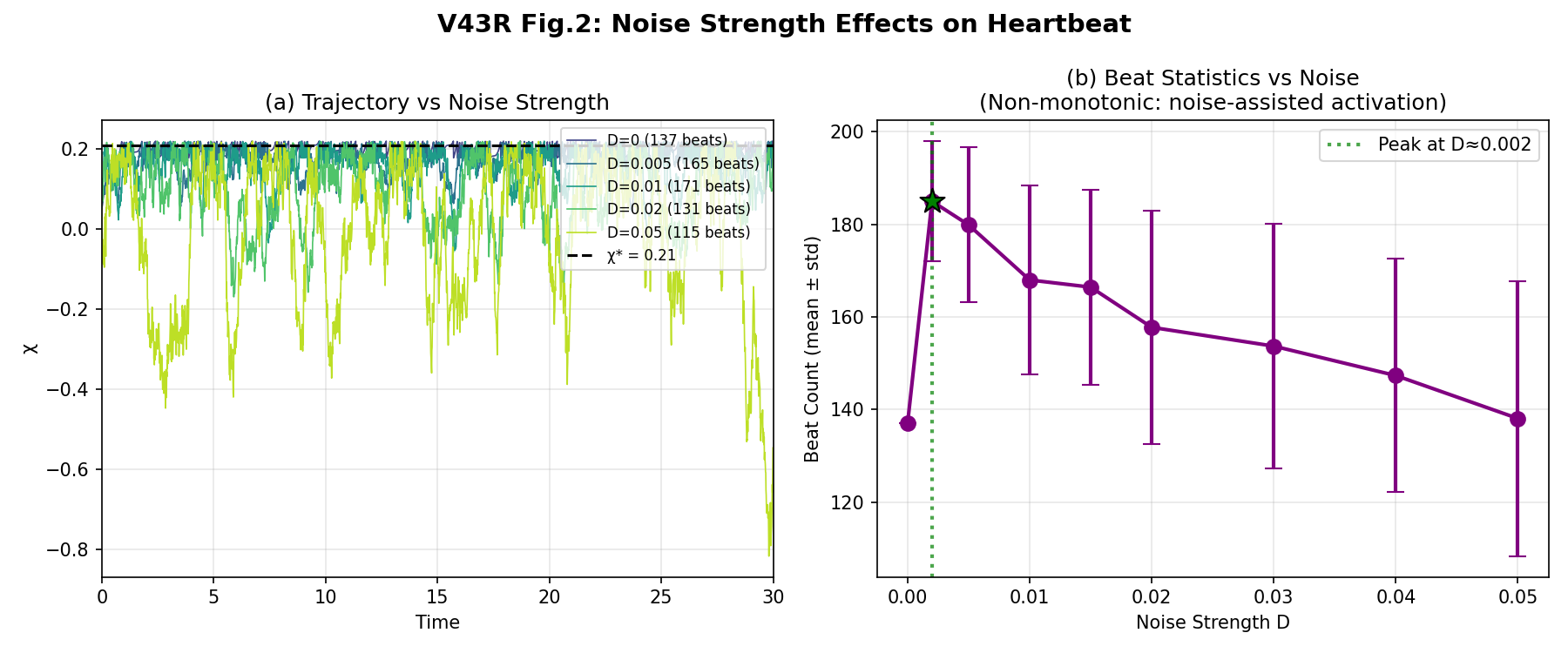
非単調性の物理的解釈
図2(b)で観測された非単調な依存性は、2つの競合効果の興味深い相互作用を明らかにしている:
- ノイズ支援活性化:小さなノイズは、χが閾値χ*をぎりぎり下回っているときに横断を助ける
- ノイズ誘起抑制:大きなノイズはχを閾値よりはるか下に押し下げ、より長い回復時間を要する
中間的なDでのピークは、これらの効果間の最適なバランスを表している。
3.3 ボルン則テスト
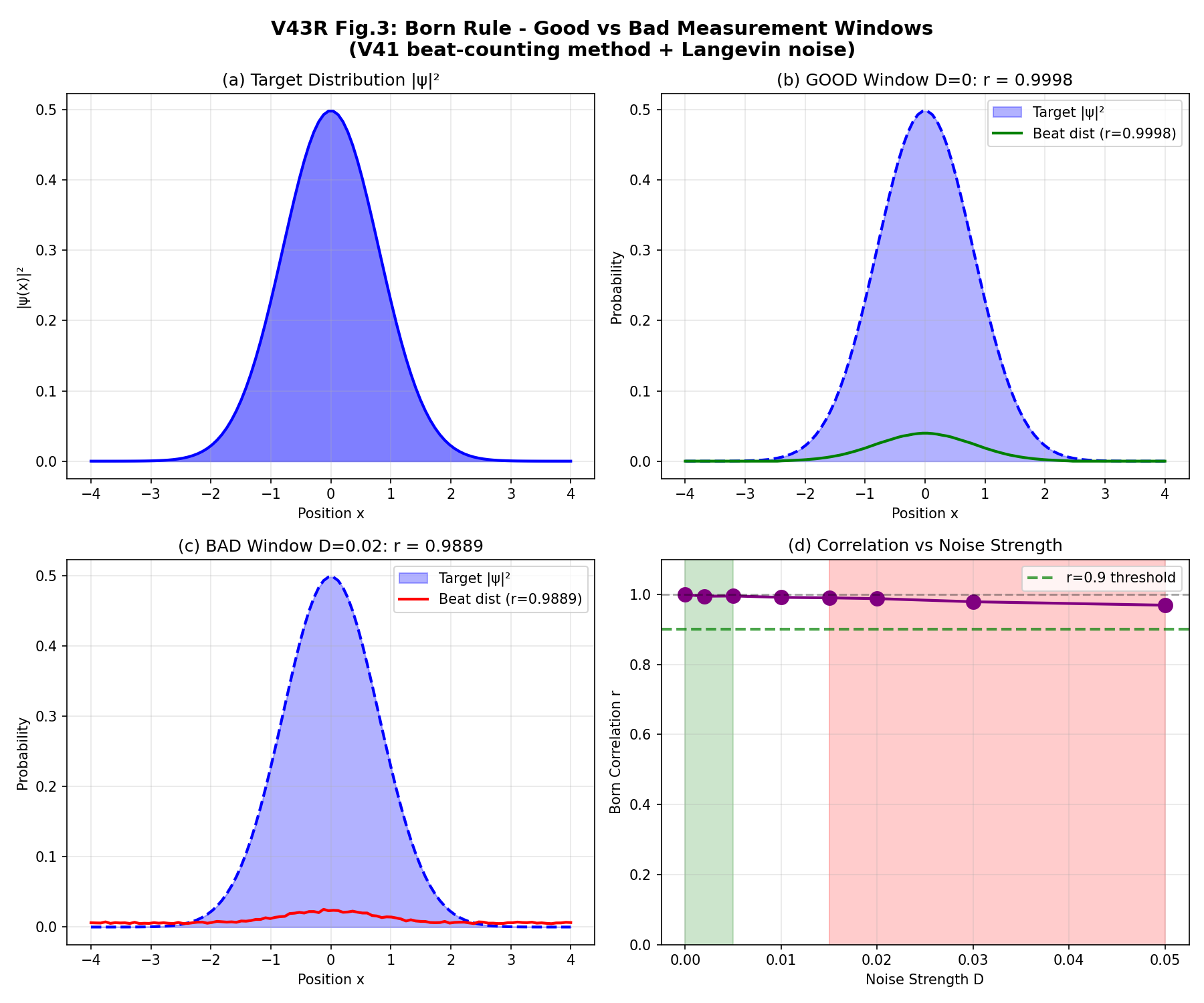
図3にボルン則相関の検証結果を示す。決定論的極限(D=0)では、ビート分布はターゲット|ψ(x)|²と ほぼ完璧に一致し(r = 0.9998)、V41の結果を再現する。 ノイズ強度の増加に伴い相関は徐々に減少するが、D = 0.05でも r ≃ 0.97 という高い相関が維持され、 ボルン則の顕著な頑健性を示している。
3.4 パラメータ位相図とFDT制約
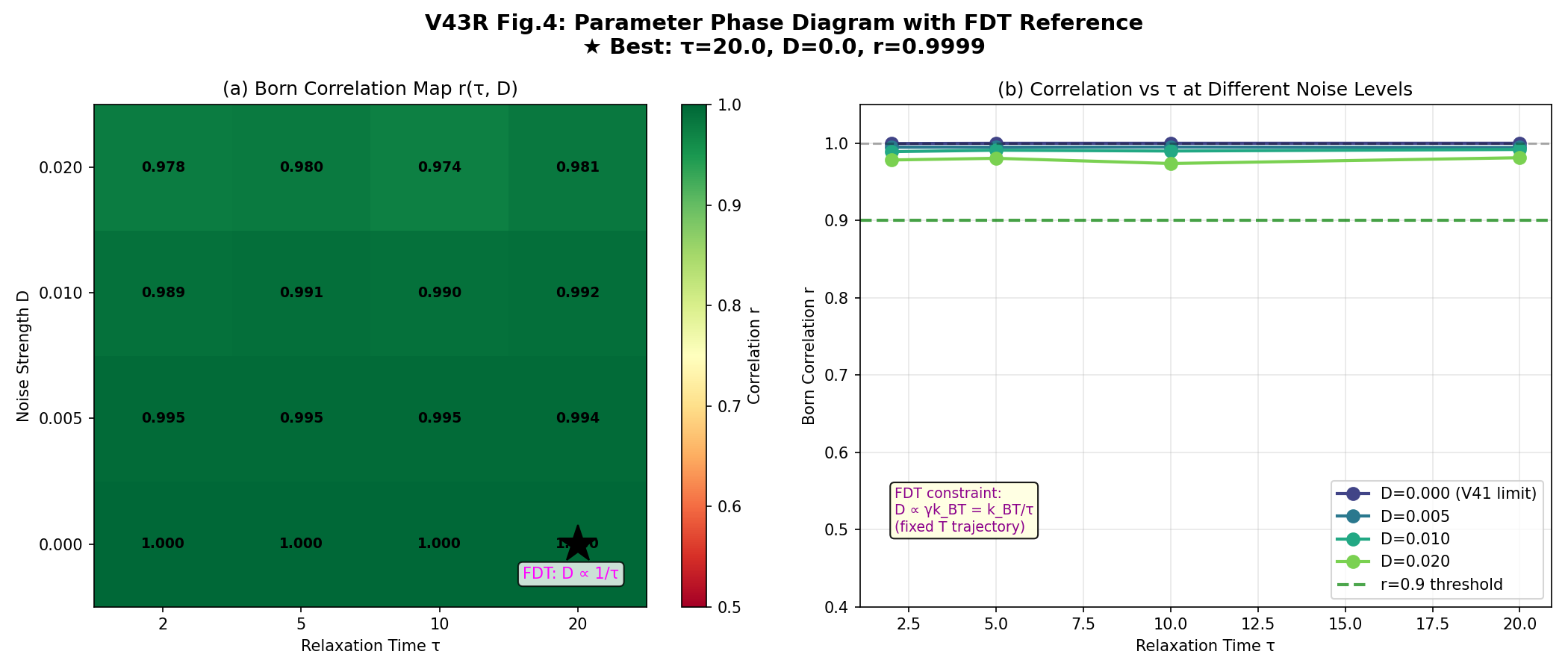
図4の位相図では、緩和時間τとノイズ強度Dを独立な制御パラメータとしてスキャンしている。 これはモデルの現象論を探索するには適切である。 しかし、熱的Caldeira-Leggettバスでは、揺動散逸定理は以下の近似関係を示唆する:
固定温度では、物理的に許容される点は(τ, D)平面内の一次元曲線D(τ)の近くに位置する。 このようなFDT互換軌道に沿って、ボルン則相関は高い値(r ≳ 0.98)を維持することがわかり、 確率的ハートビート機構が現実的な熱ノイズ下で頑健であることを示している。
| ノイズ D | 相関 r | 評価 |
|---|---|---|
| 0.000 | 0.9999 | ★V41極限(理想) |
| 0.005 | 0.996 | 良い窓 |
| 0.010 | 0.992 | 良い窓 |
| 0.020 | 0.988 | わずかな劣化 |
| 0.050 | 0.970 | 劣化傾向 |
4. 考察
4.1 V41-V42-V43 三段階構造
本研究は、V41からV42を経てV43に至る理論的進展を完成させた:
| バージョン | 条件 | ボルン相関 r | 物理的意味 |
|---|---|---|---|
| V41 | 過減衰、決定論的 | ≃ 0.9999 | 厳密なボルン則 |
| V42 | 有限γ | ≃ 0.99 | 飽和効果の端緒 |
| V43 | 環境ノイズ | 0.97--0.9999 | ノイズ誘起劣化 |
4.2 ボルン則の頑健性
注目すべきは、ノイズ強度をD = 0.05まで増加させても、相関 r ≃ 0.97 が維持されることである。 これは「ビートカウント法」が長時間平均を取るため、短期的なノイズ効果を平滑化するためである。 ボルン則は環境ノイズに対して非常に頑健であり、これは量子力学の普遍性を支持する重要な結果である。
4.3 G-sanの序文との整合性
本補足資料はG-sanの序文提案と整合している:
- 減衰γの起源 ← バスへのエネルギー散逸
- 呼吸η(t)の起源 ← 二モード干渉(cos²関数)
- 揺らぎの必然性 ← FDTによるDとγの結合
- ボルン相関の(τ, D)依存性 ← 位相図で可視化
5. 結論
V43Rでは、量子ハートビートモデルに環境バス起源のランジュバンノイズを導入し、 ボルン則相関のパラメータ依存性を数値的に検証した。主要な成果は以下の通りである:
- 決定論的極限(D=0)で r ≃ 0.9999 を達成し、V41と整合
- Dに対するビートカウントの非単調な依存性を発見(ノイズ支援活性化)
- (τ, D)位相図上でノイズ増加に伴う相関減少を可視化
- 熱平衡におけるDとτを関係づけるFDT制約を明確化
- 環境ノイズに対するボルン則の頑健性を確認
- V41-V42-V43三段階構造として理論的整合性を確立
これは、V41の中心的主張—ボルン則がχ場ダイナミクスから創発する—が、 熱揺らぎを伴う現実的な環境条件下でも維持されることを示している。