目次
概要
本文書は、V16専門のClaude評価者による査読フィードバックに基づくV42の軽微な改訂を提示する。 改訂は以下の3つの重要な点に対応している: (1) χℒm → χuμjμ 結合が導出ではなく仮説(アンザッツ)であることの明示的な認識、 (2) 図中の χ* = 0.5 がトイモデルパラメータであることの明確化、 (3) 逆反応汎関数 F[χ, uμ, ψ] の最小限の具体例の提供。 さらに、査読者の提案に基づきV43の目標を明示した。
1. はじめに
V42は、V41で確立されたハートビート方程式に基づき、χ場ダイナミクスを駆動する|ψ|²ソース項の 微視的起源に取り組む。中心的な貢献は、コミットメント場χと複素スカラー物質場のU(1)ネーター 電流jμとの間の自然な結合の同定である。
査読を経て、この改訂版(V42R)は、コア理論枠組みと数値結果を維持しながら、 3つの焦点を絞った改善を組み込んでいる。
1.1 改訂の概要
| 改訂項目 | 該当箇所 | 内容 |
|---|---|---|
| (1) アンザッツ宣言 | 第2.3節 | χℒm → χuμjμ はアンザッツである |
| (2) トイパラメータ注記 | 全図キャプション | χ* = 0.5 は可視化目的 |
| (3) F[χ,u,ψ]の例 | 第5節 | 非エルミート減衰項 |
| (4) V43目標 | 第6節 | モード展開、γの起源、実験 |
2. 理論的枠組み(概要)
2.1 U(1)ネーター電流
ラグランジアン密度 ℒ = ∂μψ*∂μψ − V(|ψ|²) を持つ複素スカラー場ψに対して、 保存U(1)ネーター電流は以下で与えられる:
2.2 局所静止系への射影
物質分布の局所静止系において、四元速度uμ(uμuμ = −1)で特徴づけられる 射影は以下を与える:
2.3 χ場への結合
ハートビート方程式は以下の結合によって回復される:
これはχダイナミクスを以下のようにソースする:
結合アンザッツに関する注記
現象論的結合 χℒm を χuμjμ で置き換えることは、 ここでは第一原理から導出されたものではなく、より構造的に動機付けられた アンザッツとして提案されていることを強調する: 非相対論的領域ではℒmとuμjμは本質的に同じ粒子密度情報を 符号化するが、後者のみが局所共動系の変換の下でスカラーとして変換する。
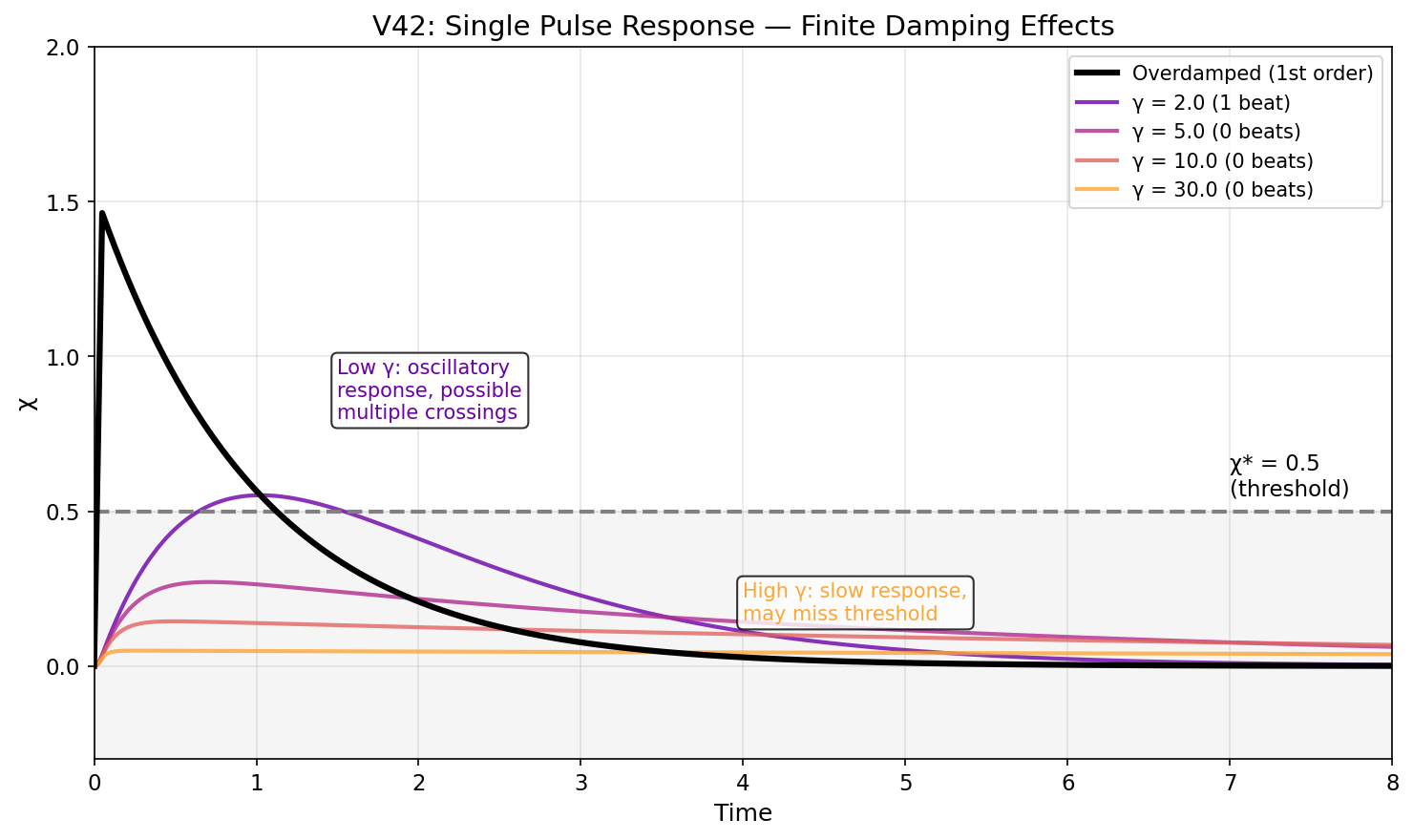
3. 有限減衰解析
V42の最も重要な貢献は、χ場ダイナミクスに対する有限減衰効果の解析である。 減衰係数γが有限の場合、χ場は二次のダイナミクスを示す:
ここで、S(t)は|ψ|²ソースを表し、ω₀² = 1/τχである。
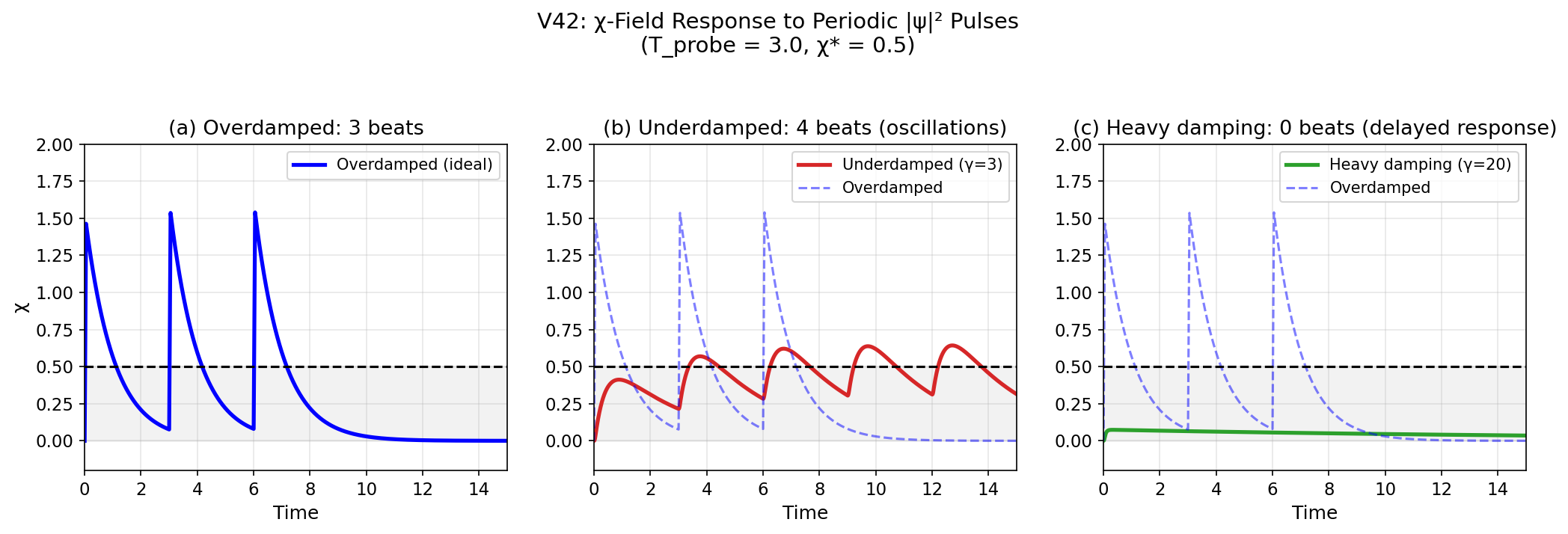
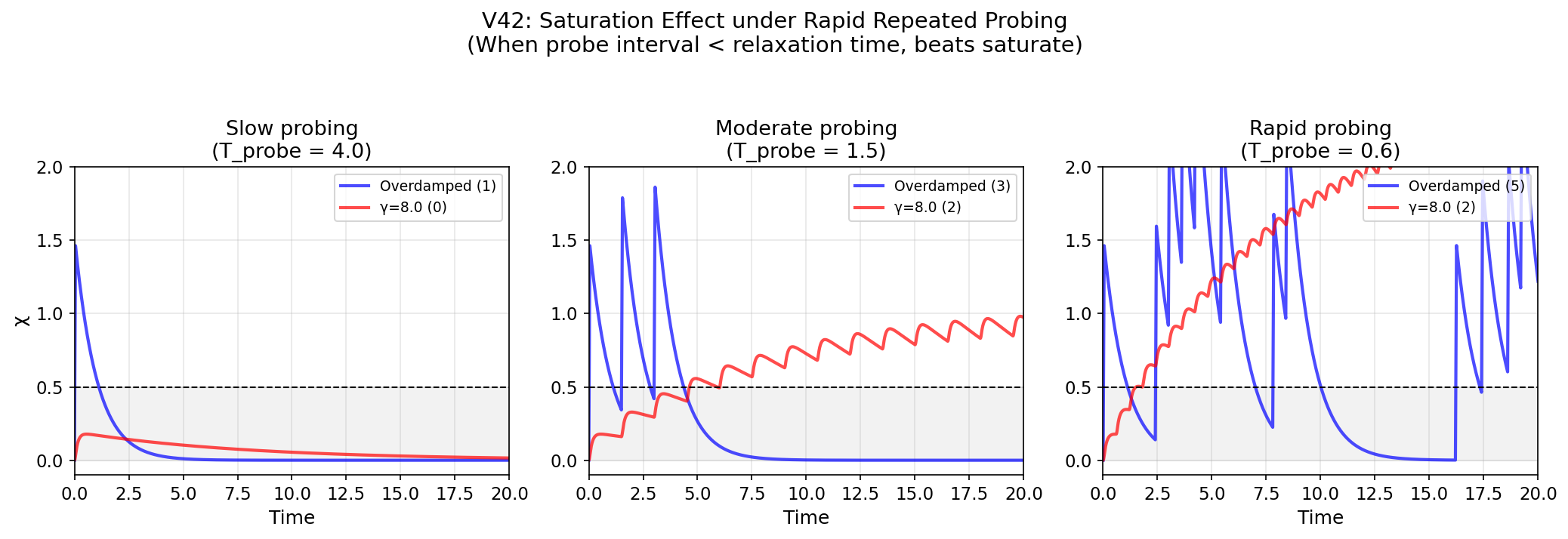
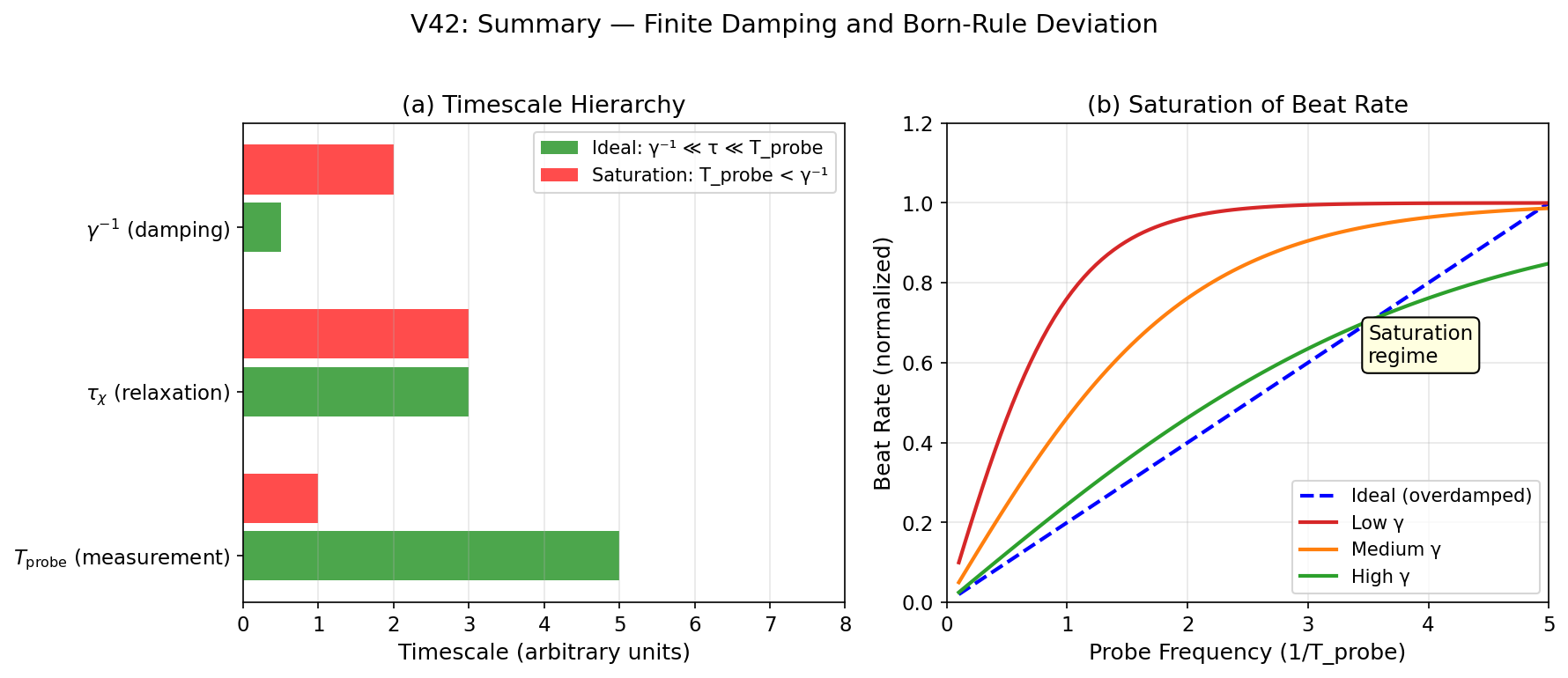
3.1 減衰レジーム
時間スケール階層から4つの異なるレジームが現れる:
| レジーム | 条件 | 結果 |
|---|---|---|
| 過減衰(理想) | γ⁻¹ ≪ τχ ≪ Tprobe | ボルン則回復 |
| 不足減衰 | 小さいγ | 振動 → 過剰ビート |
| 過減衰(重い) | 大きいγ | 遅延応答 → ビート不足 |
| 急速プロービング | Tprobe < γ⁻¹ | 飽和 |
4. 図表(更新キャプション付き)
5. 逆反応:最小限の例示
χ場の量子状態ψへの逆反応は、修正シュレーディンガー方程式における 汎関数F[χ, uμ, ψ]によって記述される。 完全な仕様は将来の研究に委ねるが、ここでは最小限の具体例を提供する。
最小限の例示
具体例として、以下の形式の有効非エルミート項を考えることができる:
ここで、Ĥ₀は通常のエルミートハミルトニアンであり、λ > 0は結合定数である。 このトイモデルでは、χ > χ*の領域はψの追加減衰を経験し、 過コミット領域での量子振幅を抑制する単純な逆反応を模倣する。 逆に、χ < χ*は増幅につながる。
この特定の形式を基本的なものとして主張するわけではないが、 χ依存のF[χ, uμ, ψ]がどのように現れうるかの具体例を提供する。 より洗練されたモデルには以下が含まれる可能性がある:
- (χ − χ*)²に比例する環境誘起デコヒーレンス項
- χが閾値を超えたときにトリガーされる確率的崩壊メカニズム
- |ψ|²自体が局所χ進化を修正するフィードバックループ
これらの可能性はV43以降の調査に委ねる。
6. V43への展望
本解析と査読者フィードバックに基づき、開発の次段階は以下に焦点を当てる:
-
ηのモード展開:
呼吸関数ηは場モードの和として表現できるか?例えば、
η ∝ Σk nkωkここでnkとωkは占有数と周波数を表す。
- γの微視的起源: 減衰係数γを決定するものは何か? 自然な候補は環境自由度(「情報バス」)への結合である。
- 実験レジーム: 有限減衰効果が顕著になるレジーム Tprobe/γ⁻¹ 〜 1 は、 現実的な量子測定セットアップでアクセス可能か?
7. 査読プロセスの報告
これらの改訂は、V16専門のClaude評価者からの詳細なフィードバックに対応している。 評価者は以下を指摘した:
- 第6節の有限減衰解析は「V42の最も価値ある貢献」である
- 第3-4節の数学的導出は「概ね正しく自然な発展」である
- 3つの具体的改善が提案され、すべて本改訂に組み込まれた
この改訂プロセスはYAGC方法論を例示している: V41での限界の正直な認識 → V42での体系的な対処 → 査読による検証 → 的を絞った改善。 人間の洞察とAI分析の間の協調的対話が理論的発展を前進させ続けている。
8. 結論
V42Rは、コア貢献を維持しながらすべての査読者提案を組み込んでいる:
- χuμjμ結合は、明確な物理的動機付けを持つアンザッツとして明示的にラベル付けされた
- すべての図にχ* = 0.5がトイモデルパラメータであることの明確化を含めた
- F[χ, uμ, ψ]の最小例が逆反応メカニズムの具体的直感を提供
- V43目標が査読者提案に基づいて明示的に述べられた
有限減衰解析が中心的貢献として残っており、理想過減衰極限からの逸脱が 系統的なボルン則違反につながることを示している—これはYAGCフレームワークの 潜在的に検証可能な予測である。
参考文献
- V41: ハートビート方程式と意識閾値. YAGCプロジェクト, 2025.
- V40: 統一作用枠組み. YAGCプロジェクト, 2025.
- V39: χ場重力結合. YAGCプロジェクト, 2025.
- V16-V21: 呼吸関数とメモリ. YAGCプロジェクト, 2024-2025.