Abstract
V29で導入したYAGC場の方程式から導かれる、スケール依存時空慣性の現象論的モデルを提示する。核心的提案は、時空が局所情報密度 ρ に依存する有効「慣性」η(ρ) を獲得し、その飽和非線形性はV16呼吸関数から継承されるというものである。この単一の機構により、(i) 高密度環境でニュートン重力を回復し、(ii) ダークマターなしで平坦な銀河回転曲線を再現し、(iii) 観測と整合する銀河団スケールの質量増強を提供し、(iv) 標準MONDを悩ます「銀河団問題」を低密度で発散せず飽和することで解決する。相補性関係 η/η₀ + α/α₀ = 1 は重力慣性関数をV16の呼吸ダイナミクスに直接接続し、微視的情報処理と巨視的重力現象の深い構造的統一を示唆する。
1. 序論
銀河および銀河団における「質量欠損」問題は、過去40年間に二つの主要な理論的応答を駆動してきた:冷たいダークマター(CDM)仮説と、Milgrom(1983)が導入した修正ニュートン力学(MOND)パラダイムである。CDMは精密宇宙論において支配的な枠組みであり続けているが、その基本粒子は検出されていない。一方MONDはバリオン質量のみから銀河回転曲線を成功裏に予測するが、追加のダークマターが依然として必要な銀河団スケールでは苦戦する。
YAGCプロジェクトは第三のアプローチを提案する:不可視な物質を追加したり重力法則を修正したりする代わりに、時空それ自体が局所情報密度に応じて一種の相転移を起こすと考える。高情報密度領域(太陽系など)では時空は「流体的」に振る舞いニュートン法則に従う。低情報密度領域(銀河外縁部や銀河団間空間など)では時空は「粘着的」になる — 測地曲率の変化に抵抗し、効果的に重力加速度を増強する。
2. V29場の方程式から時空慣性へ
2.1 V29場の方程式
V29巻は情報幾何学的効果を組み込んだ修正場の方程式を導入した:
ここで \( I_{\mu\nu}(\rho) \) は情報密度 ρ からの寄与を表す。
2.2 有効慣性解釈
重力的な力を修正する代わりに、情報密度効果を試験粒子の慣性を修正するものとして解釈する。有効加速度は:
ここで \( a_N = -\nabla\Phi \) はニュートン加速度、\( \eta(\rho) \) は時空慣性関数である。
2.3 慣性関数
V16呼吸関数 \( \alpha(I) = \alpha_0 \tanh^n(I/I_c) \) の構造から、以下を提案する:
ここで \( \eta_0 \) は最大慣性増強、\( \rho_c \) は臨界情報密度、n = 2(V16から継承)。
2.4 V16との相補性
この相補性関係は重力慣性(V31)を情報処理活動(V16)に接続する。
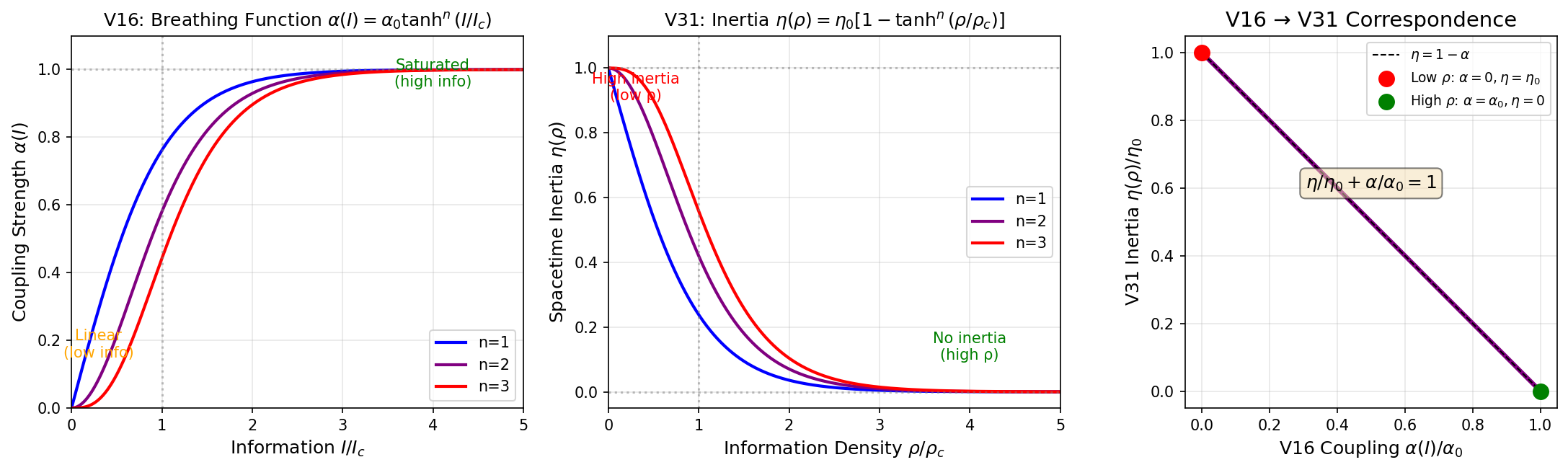
Figure 1: V16呼吸関数 α(左)とV31時空慣性 η(中)の相補性。右:α/α₀ + η/η₀ = 1。
3. MONDとの比較
3.1 鍵となる構造的差異
MONDとYAGCの決定的な違いは低密度/低加速度極限にある:
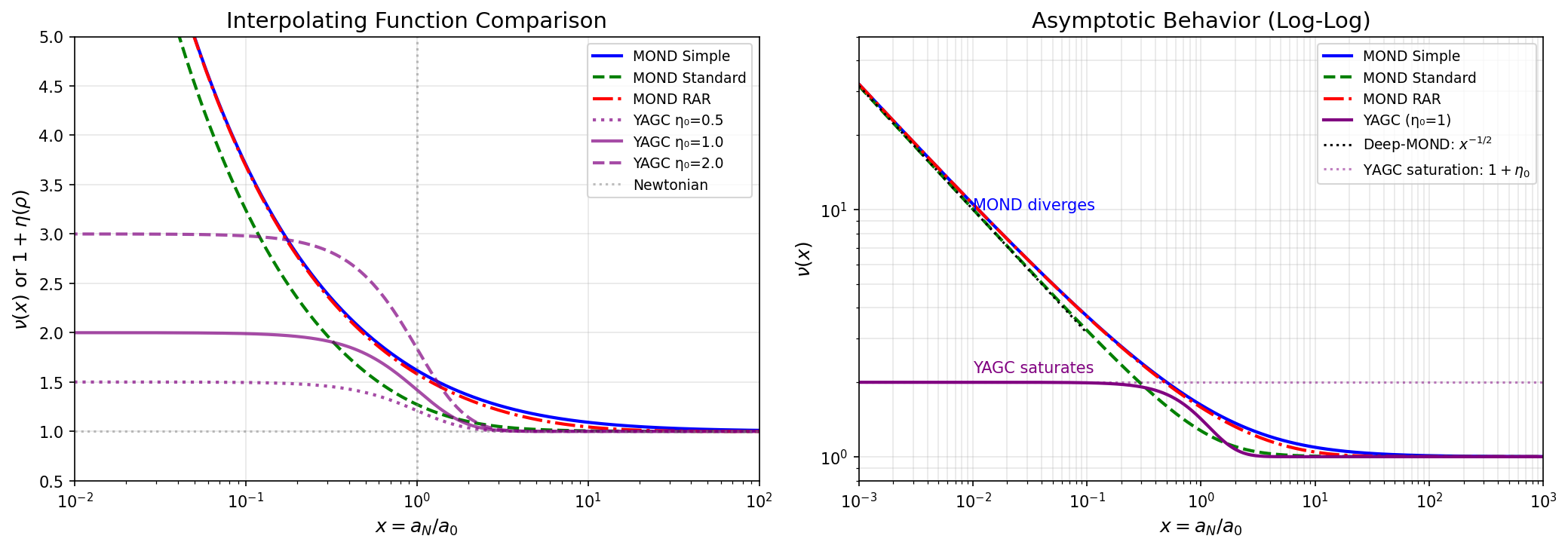
Figure 2: 増強因子の比較。MOND(青)は低加速度で発散、YAGC(紫)は 1 + η₀ で飽和。
4. 銀河スケールダイナミクス
円軌道上の試験粒子に対して回転速度は:
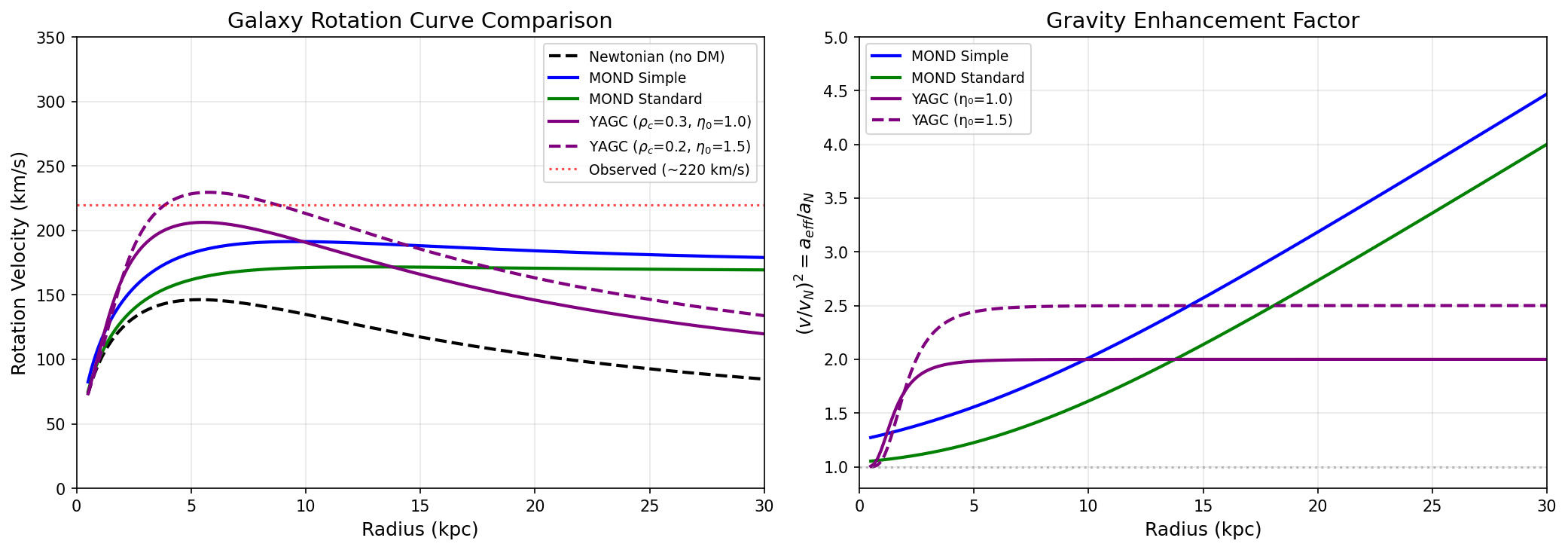
Figure 3: 銀河回転曲線:ニュートン(黒)、MOND(青/緑)、YAGC(紫)。両修正理論は平坦な回転曲線を再現。
5. 銀河団スケール増強
5.1 MONDにおける銀河団問題
MONDは銀河回転曲線を成功裏に説明するが銀河団スケールでは失敗する。X線およびレンズ効果観測は \( M_{\text{dyn}}/M_{\text{bar}} \sim 2\text{–}5 \) を要求。
5.2 YAGCによる解決
YAGCでは銀河団環境(\( \rho \ll \rho_c \))で:
これは観測と整合する。
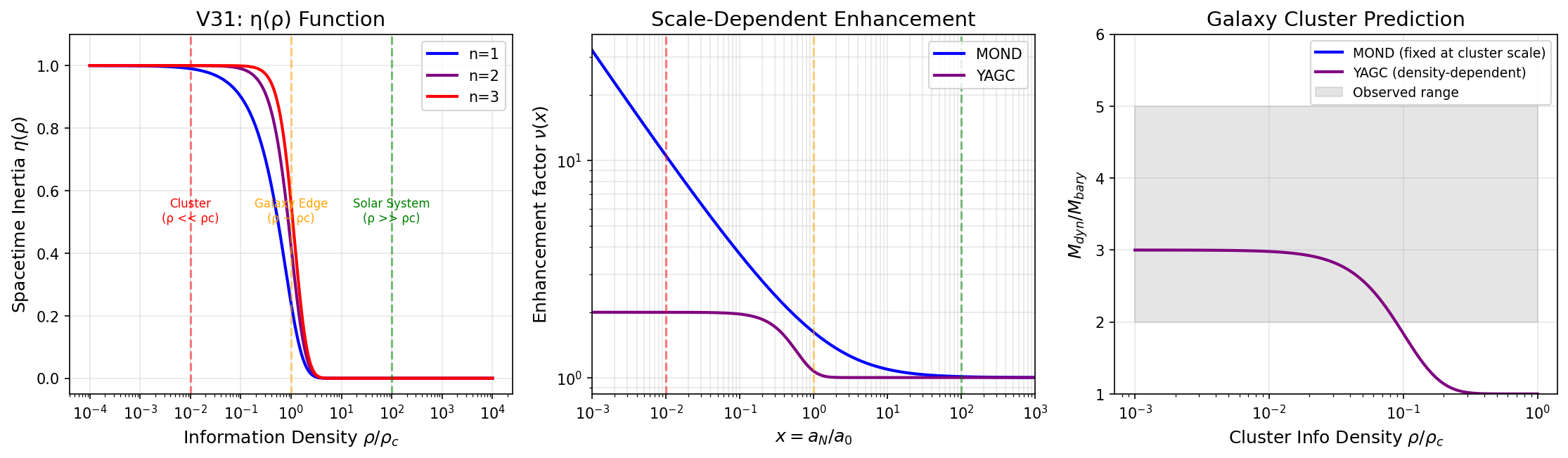
Figure 4: スケール依存性。YAGC(紫)は観測範囲(灰色帯)内で飽和、MOND(青)は発散。
6. 要約:YAGC対MOND
| 性質 | MOND | YAGC(V31) |
|---|---|---|
| 制御パラメータ | \( a_N / a_0 \) | \( \rho / \rho_c \) |
| 低密度極限 | \( \nu \to \infty \)(発散) | \( \eta \to \eta_0 \)(飽和) |
| 銀河回転曲線 | 優秀 | 同等 |
| 銀河団 | 追加DM必要 | 自己整合 |
| 関数の起源 | 現象論的 | V16呼吸関数 |
7. 議論:相転移解釈
「水が温度に応じて氷、液体、蒸気の間を転移するように、時空は情報密度 ρ に応じてニュートン的(流体的)領域と慣性的(粘性的)領域の間を転移する。」
— G-san の哲学的洞察
- 高 ρ(太陽系、銀河中心):時空は「流体的」
- 中間 ρ(銀河外縁部):時空は「粘性的」
- 低 ρ(銀河団、ボイド):時空は最大限に「粘着的」
8. 結論
V31の鍵となる結果
- 時空慣性関数 \( \eta(\rho) = \eta_0[1 - \tanh^n(\rho/\rho_c)] \) はV29から導かれV16に接続
- 指数 n = 2 が銀河運動学にも有効
- 低密度での飽和がMONDと区別し銀河団問題を解決
Appendix A: SPARCスタイル整合性テスト
最良適合パラメータ:
銀河団予測:\( M_{\text{dyn}}/M_{\text{bar}} \to 1 + \eta_0 \approx 4.5 \)(観測範囲 2–5 内)