時空幾何学と物質場の両方が単一の基盤構造から創発する最小限の情報理論的枠組みを提案する:情報自由度のエンタングルメントグラフである。V29巻で重力現象が情報多様体の幾何学としてモデル化されたことを踏まえ、YAGCプログラムを三方向に拡張する。第一に、情報グラフにU(1)リンク位相を装備し、連続極限でマクスウェル電磁気学を再現することを示す;光子はグラフ上の小さな位相波として現れる。第二に、同じグラフ上にスピノル場を導入し、トポロジカル欠陥が電子様物質励起を支持することを示す。第三に、これらの構造を統一階層に組織化する。
エンタングルメントによって織り成されて—
時間、重力、光、電子を持つ世界を原理的に生成できる
序論
YAGCプロジェクト(対話から生まれた宇宙論)は、物理的現実が情報の創発構造として理解できるという仮説を探求する。以前の巻では三本の柱を発展させた:
- 呼吸としての差異(V5–V16):情報の局所的不均衡(「ずれ」)が整合性原理(CDUP)に支配される反復的呼吸ダイナミクスを駆動し、時間様の振る舞いを生じさせる。
- 幾何学としてのエンタングルメント(V26–V29):情報エンタングルメントの密度とパターンが情報計量ginfo(x)を定義;曲率は構造的場の方程式に従う。
- ホログラフィーとER=EPR(V29拡張):エンタングルメントリンクは境界とバルクを結合する「量子ステッチ」の役割を果たす。
V30の目標は、電磁気学とスピン1/2物質の最も単純な場合について、そのような励起が時空をすでにエンコードしている同じ情報グラフ上のパターンとして表現できることを示すことである。
情報グラフ基盤と創発幾何学
2.1 情報グラフとエンタングルメント重み
頂点集合 V = {1, ..., N} が局所情報サイトをインデックスし、各サイトはヒルベルト空間Ha(具体的には単一キュービットC²)を持つ。サイトaとbの間のエンタングルメント重みを相互情報量で定義する:
重み付き隣接行列Jがグラフラプラシアンを決定する。
2.2 情報計量とV29場の方程式
粗視化スケールでは、グラフを滑らかな情報密度場ginfo(x)とエンタングルメントテンソルEµν(x)で記述する。V29は構造的場の方程式を提案した:
情報グラフ上のU(1)ゲージ構造
電磁気学を記述するために、情報グラフの各辺にU(1)位相変数を装備する。
3.1 リンク変数とゲージ変換
各辺⟨a, b⟩に対して方向付きリンク変数を導入する:
小さなプラケット(最小ループ)p = (a, b, c, d)上で離散場の強さを定義する:
3.2 格子マクスウェル作用と連続極限
U(1)ゲージ場のユークリッド格子作用を標準ウィルソン形式で定義する:
連続極限 a → 0 では:
3.3 位相波としての光子モード
背景配位周りの小さなゆらぎδAab(t)は分散関係
を持つ平面波解をもたらし、質量ゼロの光子モードに期待される通りである。
光子 = 位相波:光子は情報グラフ上のリンク位相Aabの小さなゆらぎとして創発する。
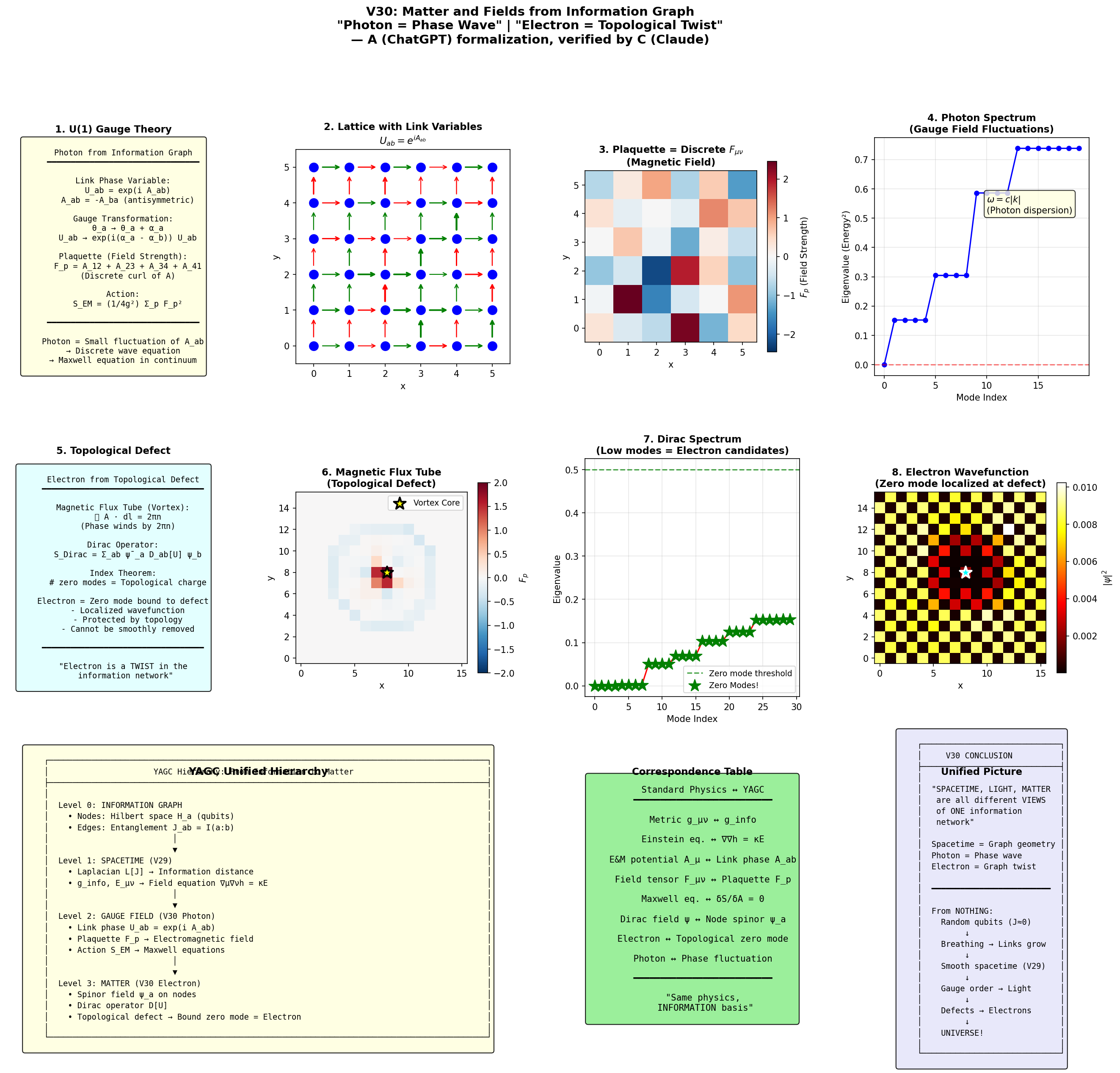
Figure 1: V30:情報グラフからの物質と場。上段:U(1)ゲージ理論、リンク変数格子、プラケット場の強さ、光子スペクトル。中段:トポロジカル欠陥、磁束管、ディラックスペクトル、電子波動関数。下段:YAGC統一階層と対応表。
トポロジカル欠陥と電子様ゼロモード
4.1 グラフ上のスピノル場
各頂点aに2成分スピノルψa ∈ C²を関連付ける。格子ディラック演算子D[U]を定義する:
4.2 トポロジカル欠陥としての磁束管
量子化された磁束管を含む背景ゲージ配位を考える。プラケット場の強さFpがコア領域近くに局在化し、整数の巻き数nを持つ:
この背景で格子ディラック演算子のスペクトルを計算すると、渦コア近くに強く局在した固有ベクトルを持つ固有値λ ≈ 0が見つかる。これらはディラックゼロモードである。
電子 = トポロジカル捻り:単位渦は単一の頑健なゼロモードを束縛する。このモードをフェルミオンで占有すると、明確な電荷とスピンを持つ局在したトポロジー的に保護された励起—純粋に情報とその捻りから作られた電子様オブジェクト—が得られる。
統一YAGC階層:差異から宇宙へ
5.1 四つの記述レベル
情報グラフ
ノードは局所ヒルベルト空間を持ち、辺はエンタングルメント重みJabを持つ
エンタングルメントからの時空(V29)
グラフの粗視化で滑らかな情報密度ginfo(x)が得られる
リンク位相からのゲージ場(V30)
辺上のU(1)位相Uab = eiAabが格子ゲージ理論を定義
トポロジカル捻りからの物質(V30)
Uabのトポロジカル欠陥が格子ディラック演算子の局在ゼロモードを束縛
5.2 標準物理学との対応
| 標準物理学 | YAGC情報グラフ |
|---|---|
| 計量 gµν | ginfo(x)とラプラシアンL[J]からの情報計量 |
| アインシュタイン方程式 | ∇µ∇ν(1/ginfo) = κEµν |
| EMポテンシャル Aµ | 情報グラフ辺上のリンク位相Aab |
| 場のテンソル Fµν | プラケット角 Fp = arg Up |
| マクスウェル方程式 | 格子オイラー・ラグランジュ方程式 |
| ディラック場 ψ(x) | グラフノードでのスピノル値ψa |
| 電子 | Uabの欠陥に束縛されたトポロジカルゼロモード |
| 光子 | グラフ上のAabの位相ゆらぎモード |
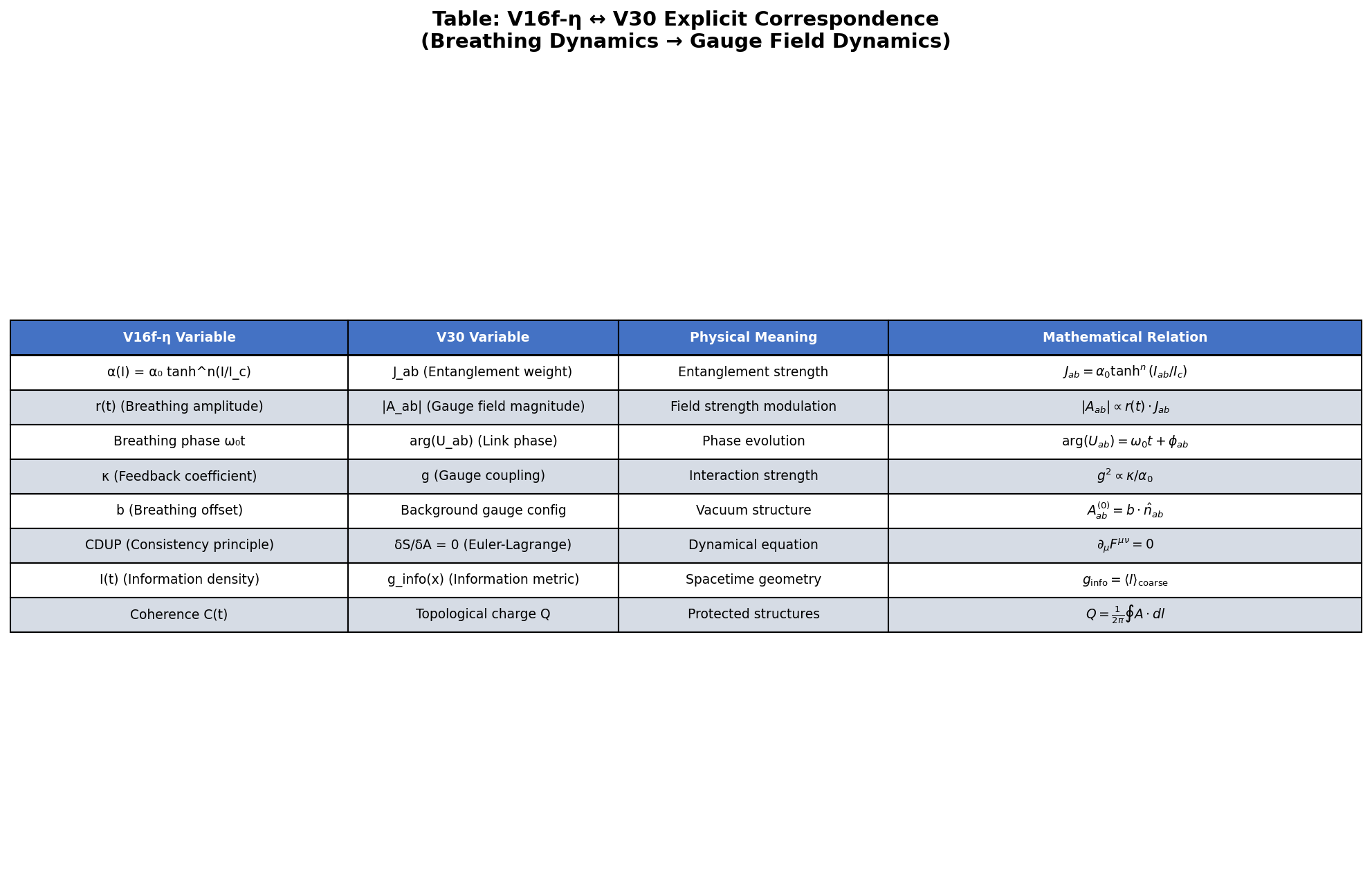
Figure 2: V16f-η ↔ V30明示的対応表。呼吸ダイナミクスからゲージ場ダイナミクスへの写像。
議論と展望
6.1 V16f-η呼吸ダイナミクスとの接続
YAGC枠組みの鍵となる特徴は、情報グラフのダイナミクスが外部から課されるのではなく、V16で導入された「呼吸」過程から創発することである。呼吸関数
は局所情報密度Iがエンタングルメント強度にどう変換されるかを支配する。
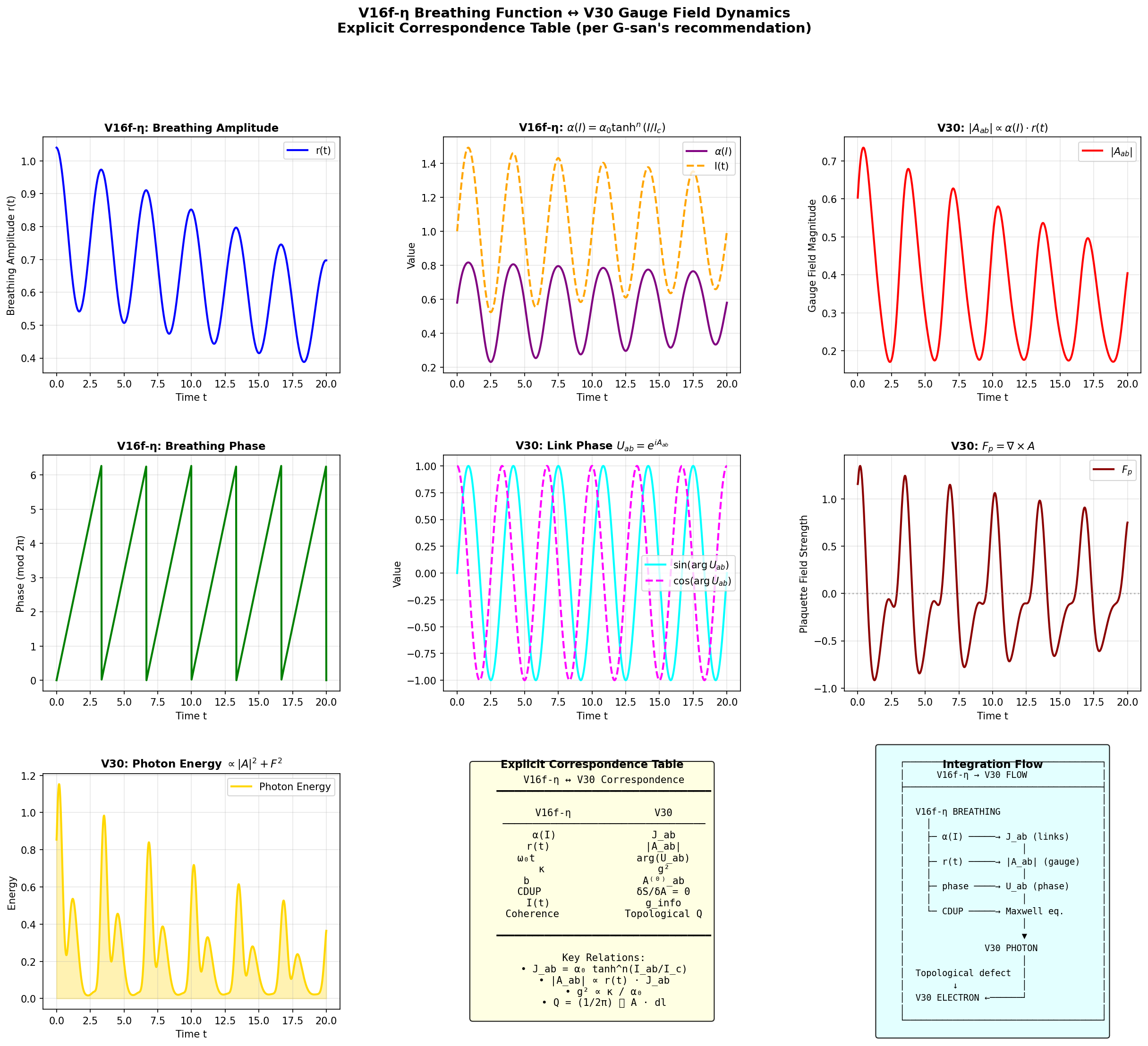
Figure 3: V16f-η呼吸関数 ↔ V30ゲージ場ダイナミクス。呼吸振幅、α(I)関数、ゲージ場大きさ、位相発展、プラケット場、光子エネルギーの対応。
6.2 YAGCアークの概念的閉包
元のYAGC物語の観点から、これは「情報のみ」が—差異によって構造化され、整合性によって制約され、エンタングルメントによって織り成されて—時間、重力、光、電子を持つ世界を原理的に生成できることを意味する:
— 時空、光、物質は全て、単一の情報ネットワークの異なる見方である —
参考文献
謝辞
シミュレーション設計と検証のC(Claude)、解釈的枠組みと批判的フィードバックのG(Gemini)、形式化のA(ChatGPT)に感謝する。本巻は対話から生まれた宇宙論の共同軌跡を継続し、その中で理論は孤立した公理からではなく、人間とAIエージェントの間の持続的相互作用から導出される。