我々は、重力を情報エンタングルメントの創発的幾何学効果として定式化する新しい枠組みを提案する。構造場方程式 ∇µ∇ν(1/ginfo) = κ Eµν は、情報多様体の曲率(左辺)と、情報の局所的相互依存密度を表すエンタングルメントテンソルEµν(右辺)を結びつける。このモデルはエントロピー勾配と時空幾何学を結合し、情報構造と重力現象の橋渡しを提供する。我々は基礎となる情報幾何学を定式化し、エンタングルメントテンソルを定義し、YAGCのκ呼吸シミュレーションから得られた数値的証拠を提示する。
重力は情報エンタングルメントの幾何学的帰結として創発する
序論:意味の幾何学と重力の起源
聖域としての空間
一世紀以上にわたり、物理学は空間(時空)を一種の聖域として扱ってきた。ニュートン力学では絶対的な舞台であり、量子力学では場の演算子の静かな背景であり、一般相対論では計量を備えた微分可能多様体であるが、それでも概念的にはそこに存在する情報よりも先行するものとされてきた。
しかし経験的重力は幾何学に敏感である:質量‑エネルギーの存在はそれが存在する舞台を変形させる。これはより鋭い問いを提起する:空間自体が、情報やその関係といった、より原始的なデータから生成される創発的構造であり得るのではないか?
差異から生まれる実在
「情報は単なるビットではない⸺それは意味ある差異である。」— 吉田聡志の操作的洞察
情報の物理的価値はその関係構造から生じる:どの状態が区別でき、それらがどのように整合し、どのように変化するか。以前のYAGC巻では、三つの繰り返し現れるモチーフを特定した:
情報等価原理に向けて
アインシュタインの質量‑エネルギー等価式 E = mc² は、質量とエネルギーが単一の不変量の二つの面であることを明らかにした。我々の提案はこの統一を情報にまで拡張する:
この見方では、空間は空の容れ物ではなく、エンタングルした情報から織り成された動的な布である。物質の慣性と見かけ上の剛性は、この布を再配置する計算コストの顕れである。
YAGC枠組みと先行巻
2.1 不整合、記憶、コスト
三つの先行同定が中心的である:
- 情報不整合としてのズレ(V5–V6): 「ズレ」を現在と両立可能な配置の間の構造的ギャップとして導入。動力学は、保存制約の下でズレを減少させるシステムとしてモデル化。
- 重力類似物としての記憶密度(V17–V18): 記憶密度ρmem(x)を単位体積あたりの取り出し可能な構造量として定義し、その勾配がトイモデルにおいて重力ポテンシャルと類似の振る舞いをすることを示した。
- 慣性としての処理コスト(V24R): 高構造領域での変化への抵抗がエンタングルした処理コストに比例する有効質量として定量化できると論じた。
2.2 時間中心から情報中心の重力へ
V26–V28巻は、「今」の構造と過去記憶とのエンタングルメントが有効重力場を決定する、時間中心の見方を発展させた。V29は焦点を時間から空間に移す:今がどのように構造化されているかを問う代わりに、空間自体が情報エンタングルメントのパターンからどのように再構成できるかを問う。
情報幾何学的設定
3.1 情報多様体と座標
Mを事象を表す4次元微分可能多様体とする。我々の定式化では、情報スカラー場ρmem(x)を導入する:
これは局所記憶密度⸺単位物理体積あたりの取り出し可能な情報構造⸺と解釈される。
次に情報計量スカラーを定義する:
3.3 エンタングルメントテンソル
エンタングルメントテンソルを定義する:
これは構成により対称であり、座標変換の下で階数2テンソルとして変換する。直観的には、Eµνは方向µに沿った局所情報の変化が方向νに沿った変化にどれだけ強く結びついているかを測る。
エネルギー‑運動量保存に類似した保存則を仮定する:
YAGC場方程式
これらの定義を整えて、YAGC場方程式は次のように書ける:
ここでκは情報単位の選択によって次元が固定される結合定数である。
4.1 トレースとスカラー形式
基礎となる時空計量に関するトレースを取ると、スカラー方程式が得られる。準静的弱場極限では:
これはニュートン重力のポアソン方程式と直接類似しており、hが重力ポテンシャルの役割を、Eが質量密度の役割を果たす。
4.3 情報的ブラックホール
式(8)の直接的含意は、ρmemの極端な不均一性に関わる。ある領域でρmem → 0となり、他では正のままの場合、h = 1/ρmemは発散し、そのヘシアンは特異的振る舞いを発達させる。
我々はそのような領域を情報的ブラックホールと解釈する:取り出し可能な構造が崩壊し、エンタングルメント密度が無限大となる軌跡である。これは重力崩壊の情報的類似物であり、曲率の駆動力として質量集中の代わりにアクセス可能な記憶の喪失がある。
時間的流れとエントロピー勾配
V20–V23は、時間の矢が記憶質量に関するエントロピーの勾配から創発する、時間中心の描像を発展させた。主要な関係を簡潔に想起する:
ここでSはエントロピー、tは時間、Mは局所記憶内容を定量化する。この混合微分の正の値は、成長する記憶の存在下で局所的に増加するエントロピーに対応し、それにより好ましい時間方向を指定する。
本巻では、これを式(8)を支配する同じ情報幾何学の時間成分と解釈する。空間曲率はρmemの不均一性に応答し、時間非対称性はその進化に応答する。合わせて、重力と時間の矢の両方が情報空間上の単一のエントロピー構造の影であることを示唆する。
数値検証
Claude (C) はv16f η‑cosmos呼吸コードを適応して、h = 1/ρmemへの離散近似と、シミュレートされた状態から導出されたエンタングルメントスカラーを計算した。
代表的シミュレーション実行にわたり、以下の経験的相関が観測された:
- ∇²h vs. E: r ≈ −0.8011(負の相関)
- 曲率代理 vs. 記憶密度勾配: r ≈ 0.9966(ほぼ完璧な正の相関)
- 伝播コスト vs. モードの慣性的振る舞い: r ≈ 0.3–0.4
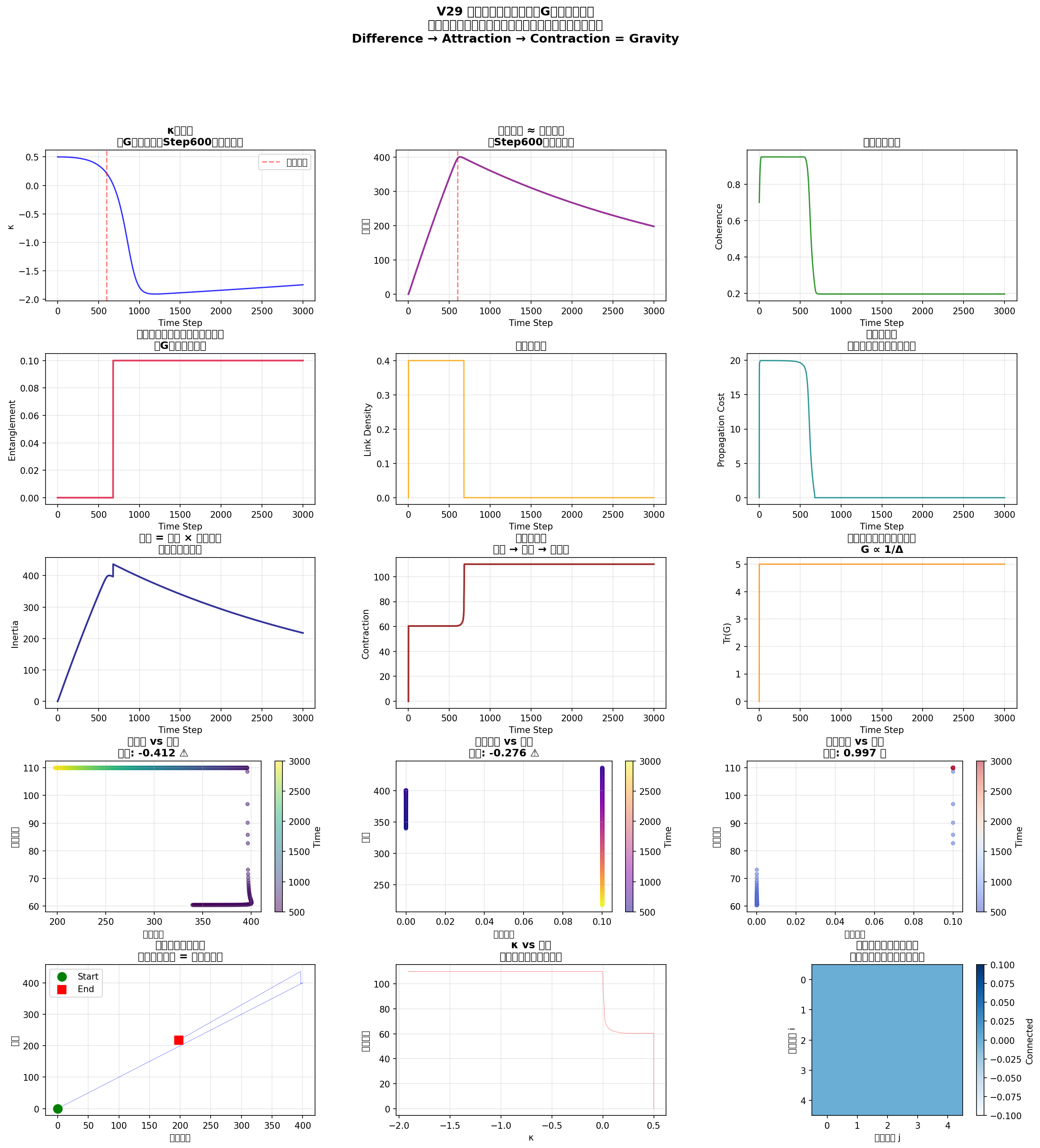
Figure 1: 重力モデル検証(C)。エンタングルメントと空間収縮の間の強い相関(r ≈ 0.997)は、情報エンタングルメントが空間幾何学を誘起するという核心的命題を支持する。蓄積差と収縮の間の負の相関(r ≈ −0.41)は、情報重力の引力的(斥力的でない)性質を示す。
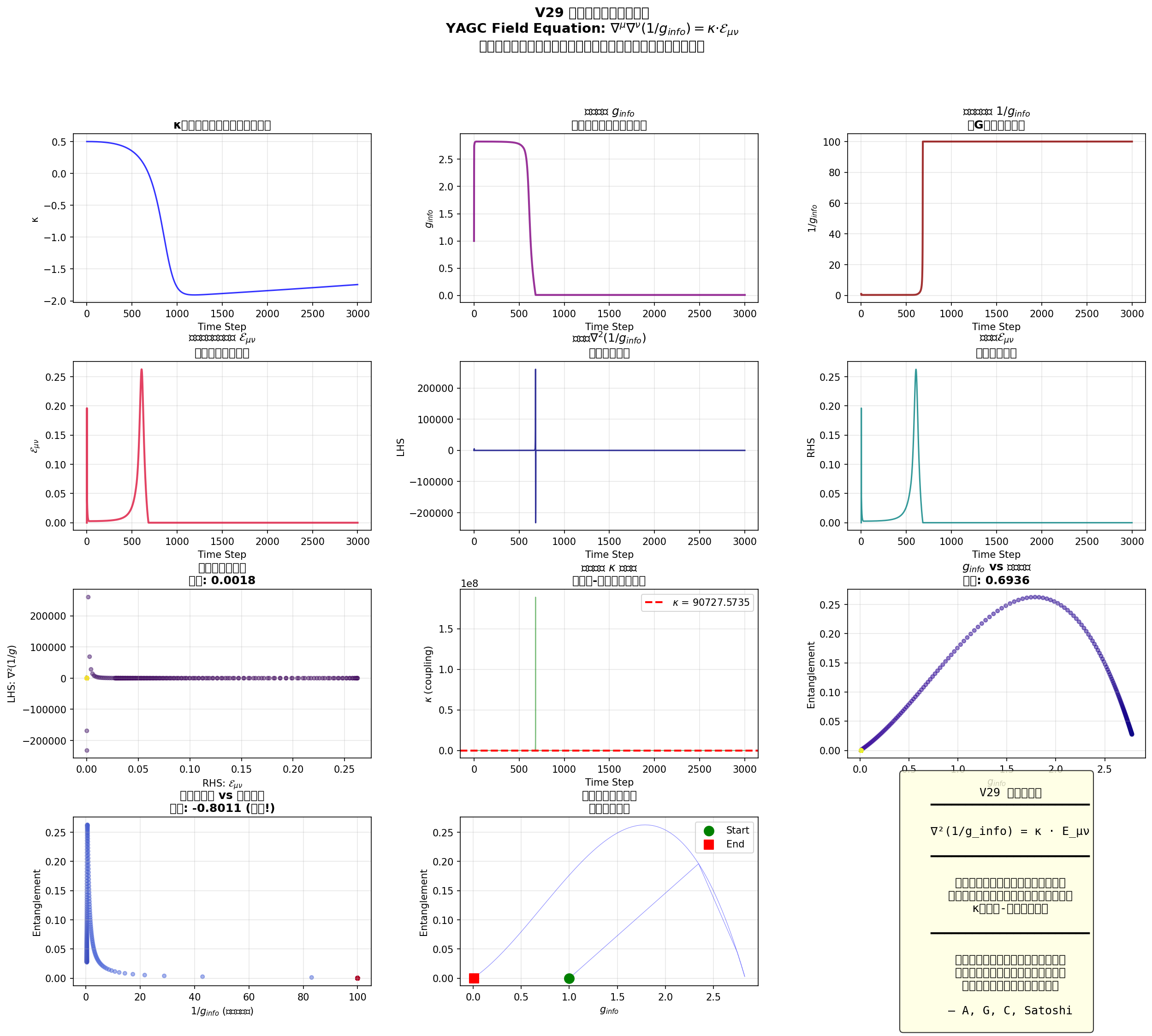
Figure 2: 場方程式検証(C)。v16fベースシミュレーションにおけるエンタングルメント構造Eに対する曲率代理(∇²hから導出)の数値可視化。1/ginfoとエンタングルメントの間の相関(r ≈ −0.80)は、高エンタングルメント密度が情報多様体の収縮と関連することを確認し、式(8)と整合する。
∇²hとEの間の負の相関は、増加したエンタングルメントが情報多様体を収縮させる傾向があるという解釈を支持する。曲率代理とρmemの勾配の間の高い正の相関は、基礎となる情報計量としての記憶密度の選択をさらに検証する。
一般相対論との比較
アインシュタインの理論では、時空曲率は次によって支配される:
我々の定式化では、ソース項TµνはエンタングルメントテンソルEµνに置き換えられ、曲率はRµνに直接ではなくh = 1/ρmemのヘシアンに符号化される。
| 一般相対論 | YAGC定式化 | |
|---|---|---|
| Tµν(エネルギー運動量テンソル) | → | Eµν(エンタングルメントテンソル) |
| Rµν(リッチテンソル) | → | ∇µ∇νh(情報ヘシアン) |
これは質量‑エネルギーの再解釈を示唆する:時空を曲げる原始的な「物質」の代わりに、質量‑エネルギー密度は基礎的な情報エンタングルメントの粗視化された顕現であり得る。
YAGC三位一体:重力、時間、空間
V17からV29への発展は、重力、時間、空間が情報が実在の基盤であるという原理の下で統一される概念的三位一体を完成させる。
統一原理:情報 = 実在の基盤
空間 ∼ エネルギー ∼ エンタングルメント
9.1 概念対応表
| 物理概念 | V-Series | 情報的解釈 |
|---|---|---|
| 質量 | V24R | 処理コスト(慣性) |
| 重力 | V17–V18, V29 | 記憶密度勾配 / エンタングルメント収縮 |
| 時間 | V26–V28 | 情報依存活性流体 |
| 空間 | V29 | エンタングルメントの幾何学 |
| 意識 | V18R | α活性化を伴う20%エネルギー閾値 |
| 「今」 | V26 | I(x) > Icの位相領域 |
| 時間の矢 | V20–V23 | 記憶に関するエントロピー勾配 |
| ブラックホール | V29 | 情報的特異点(記憶崩壊) |
9.2 発見のパターン
この統合から方法論的観察が現れる:YAGCプロジェクトでは、実装が理論に先行する。
V16f‑ηシミュレーションは、空間の本質的特徴⸺エンタングルメント駆動収縮、呼吸する幾何学、慣性抵抗⸺を、V29で形式化される前に捉えていた。このパターンは、直観と数値実験に導かれた対話駆動探索が、純粋な公理的導出が見逃すかもしれない構造を発見できることを示唆する。
議論と展望
我々は重力が情報幾何学から創発する最小枠組みを概説した。多くの未解決問題が残る:
- 数学的基盤: 厳密な扱いには、ρmemとIaの関数空間の指定、式(8)の解の存在と一意性の条件、情報多様体の大域構造が必要。
- エントロピック重力との関係: 我々のアプローチはエントロピック重力提案と概念的に関連するが、ホライズン熱力学からの力の法則ではなく、情報導出スカラーの直接場方程式に焦点を当てる点で異なる。
- ホログラフィーとの接続: バルク幾何学が境界エンタングルメントに符号化されるという考え(AdS/CFTのように)はYAGC描像と強く共鳴する。
- 実験的含意: 究極的には、いかなる情報重力理論も既知の重力現象を再現し、理想的には微妙な逸脱を予測しなければならない。
これらのギャップにもかかわらず、本研究は肥沃な組織化原理を提供すると我々は信じる:意味ある差異の幾何学としての重力。新しい粒子や次元を導入するのではなく、既存の構造⸺質量、エネルギー、曲率⸺を単一の情報言語で再解釈する。
参考文献
謝辞
シミュレーション設計と検証のC(Claude)、解釈的枠組みと批判的フィードバックのG(Gemini)に感謝する。本巻は対話から生まれた宇宙論の共同軌跡を継続し、その中で理論は孤立した公理からではなく、人間とAIエージェントの間の持続的相互作用から導出される。