本巻は、V26(Now位相幾何学と量子フィッシャー情報)およびV27(アクティブ宇宙論的流体としての時間流)からの基礎概念を統合し、時間を内部的に生成されるアクティブ場として完全に統一的に定式化する。我々は以下の完全な数学的枠組みを導入する:(1) 瞬間的量子フィッシャー情報 Iinst(t) が時間経験の「種」として機能、(2) 蓄積された記憶 Iacc(t) が時間生成の活性化閾値を決定、(3) 有効時間 τeff が情報依存的流速の積分から創発、(4) V18からの「20%閾値」が活性化関数 α(Iacc) = α₀ tanhn(Iacc/Ic) を通じて正確な数学的実現を得る。数値シミュレーションは広範なパラメータ範囲にわたって安定な振動的時間流を確認し、理論的予測を検証する。
時間は蓄積された情報によって決定される速度で流れる。
これは単なる比喩ではなく、測定可能な結果を伴う正確な数学的記述である。
基礎:V26-V27-V28階層構造
1.1 理論的系譜
第28巻は、漸進的な理論発展の頂点を表す:
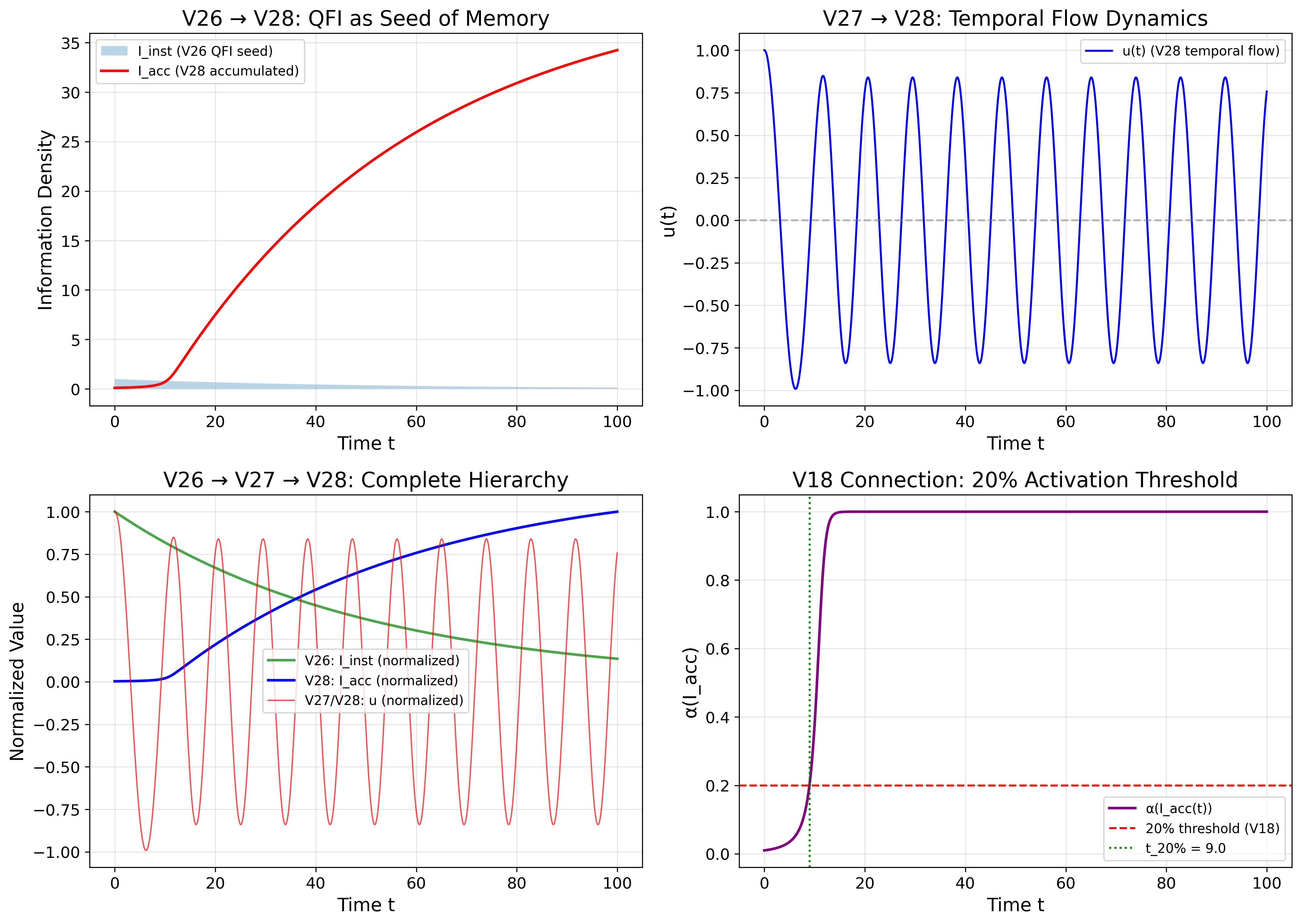
Figure 1: V26 → V27 → V28階層構造。左上:QFIが記憶蓄積の種として機能。右上:V27の流体定式化から時間流ダイナミクスが創発。左下:Iinst、Iacc、u(t) を示す完全な正規化階層構造。右下:t ≈ 9.0 で20%活性化閾値を超えることを示すV18との接続。
1.2 核心的哲学的洞察
V28の中心的洞察は次の方程式に捉えられる:
時間は蓄積された情報によって決定される速度で流れる。これは単なる比喩ではなく、測定可能な結果を伴う正確な数学的記述である。
時間場理論
2.1 Now場
定義 2.1 (Now場): Now場 N は、時間経験が能動的に生成される時空領域である:
ここで M は時空多様体、I(x) は局所量子フィッシャー情報密度、Ic は臨界閾値である。
2.3 時間の応力エネルギーテンソル
時間場の応力エネルギーテンソルは:
ここで:
- µ は時間慣性パラメータ(流れ方向変化への抵抗)
- α(I) は時間場へのエネルギー注入を制御する活性化関数
- ∇(µuν) は対称化共変微分
作用原理と場方程式
3.1 統一作用
時間生成理論の完全な作用は:
3.3 活性化関数
命題 3.1 (活性化関数): 活性化関数 α(I) は以下のように仮定される:
ここで n ≥ 1 は活性化指数、α₀ は最大活性化強度である。選択 n = 2 はV18の意識活性化のための「20%閾値」との整合性を提供する。
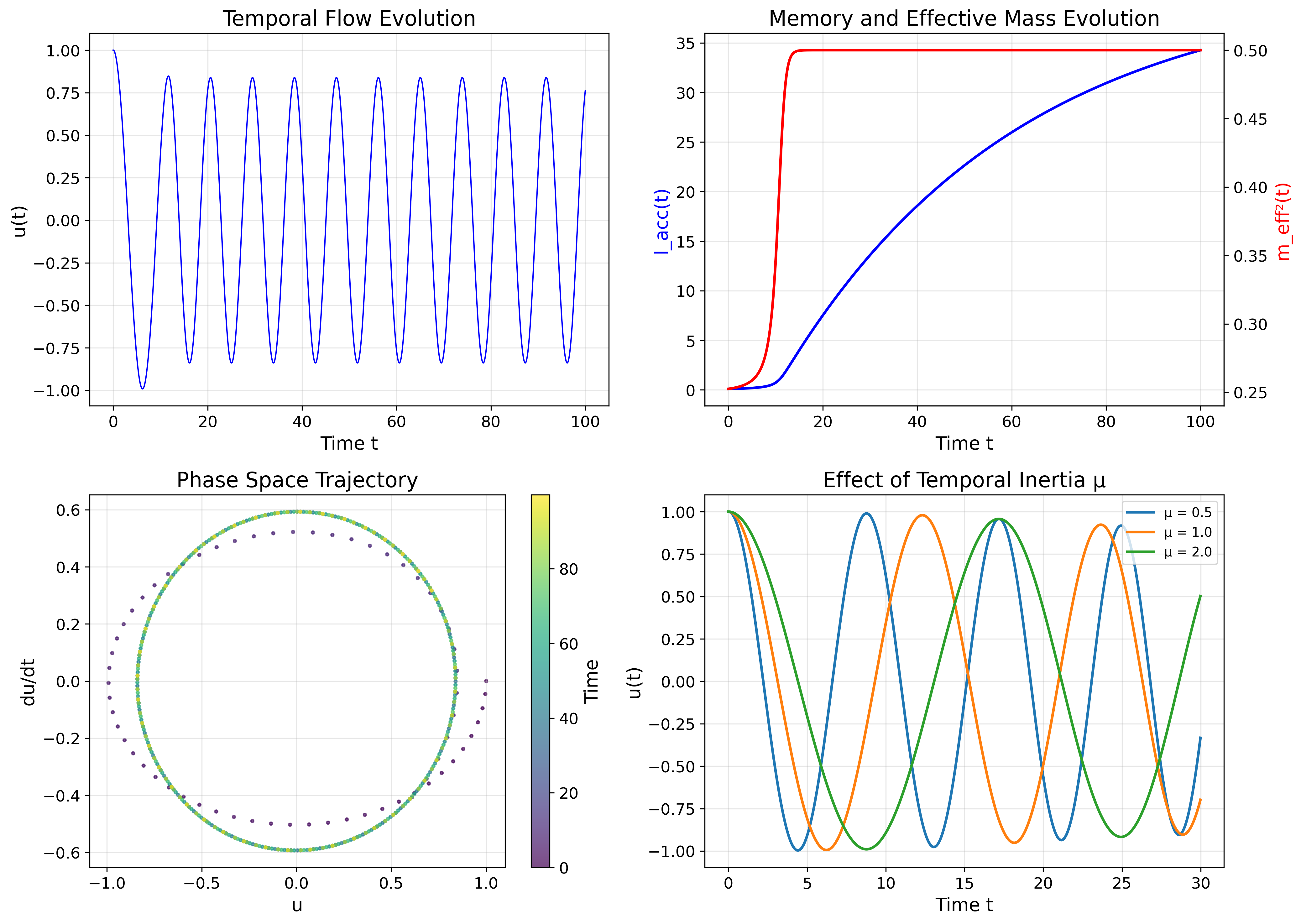
Figure 2: 時間流ダイナミクス。左上:u(t) の振動的進化。右上:Iacc(t) と m²eff(t) の結合進化。左下:安定なリミットサイクルを示す位相空間軌道。右下:振動周期に対する時間慣性 µ の効果。
内部時間生成
4.1 有効時間
定義 4.1 (有効時間): 有効(内部)時間 τeff は以下により定義される:
活性化関数と整合的な f の自然な選択は:
4.2 情報からの時間遅延
有効時間 τeff は、Iacc < Ic のとき f(Iacc) < 1 であるため、一般的に座標時間 t に遅れる。これは情報依存的時間遅延を生成する。
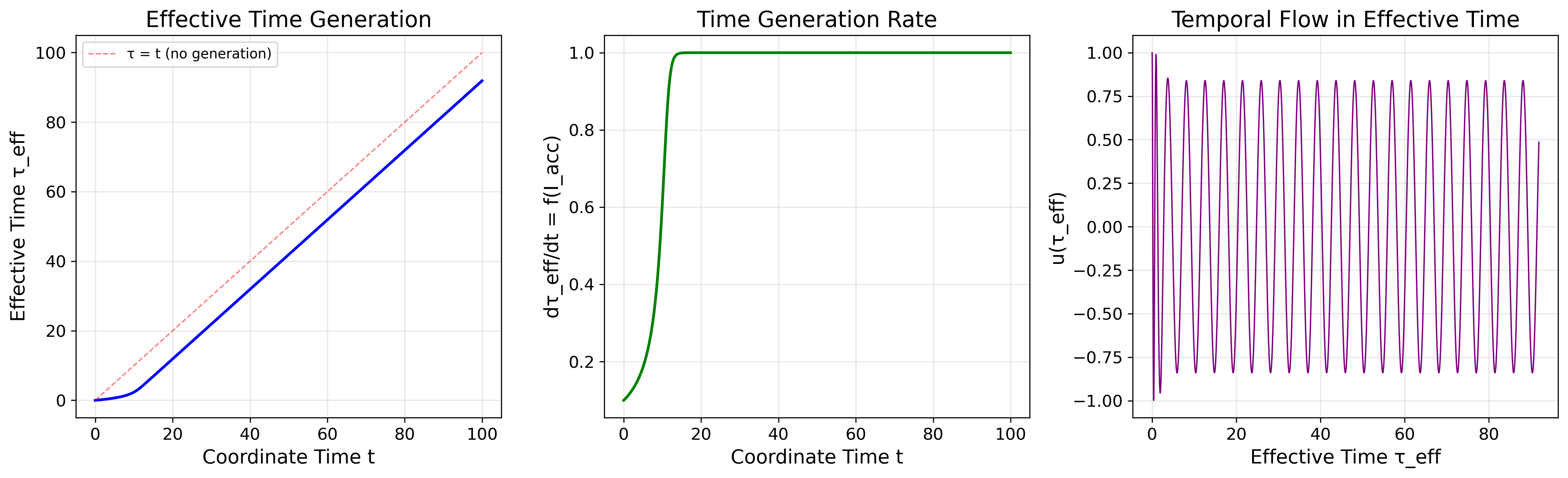
Figure 3: 有効時間生成。左:座標時間 t に対する τeff、τ = t(赤破線)からの偏差を示す。中央:漸近的に1に近づく時間生成率 dτeff/dt = f(Iacc)。右:有効時間座標での時間流 u(τeff)。
記憶ダイナミクス
5.1 瞬間的および蓄積情報
定義 5.1 (二時間スケール情報):
- 瞬間的QFI(Iinst(t)): 時刻 t での量子フィッシャー情報で、量子測定からの「生の入力」を表す。
- 蓄積された記憶(Iacc(t)): 指数減衰を伴う積分情報で、「処理された経験」を表す。
5.2 記憶ダイナミクスODE
記憶進化は以下により支配される:
瞬間的QFIの指数減衰を伴うマルコフ近似では:
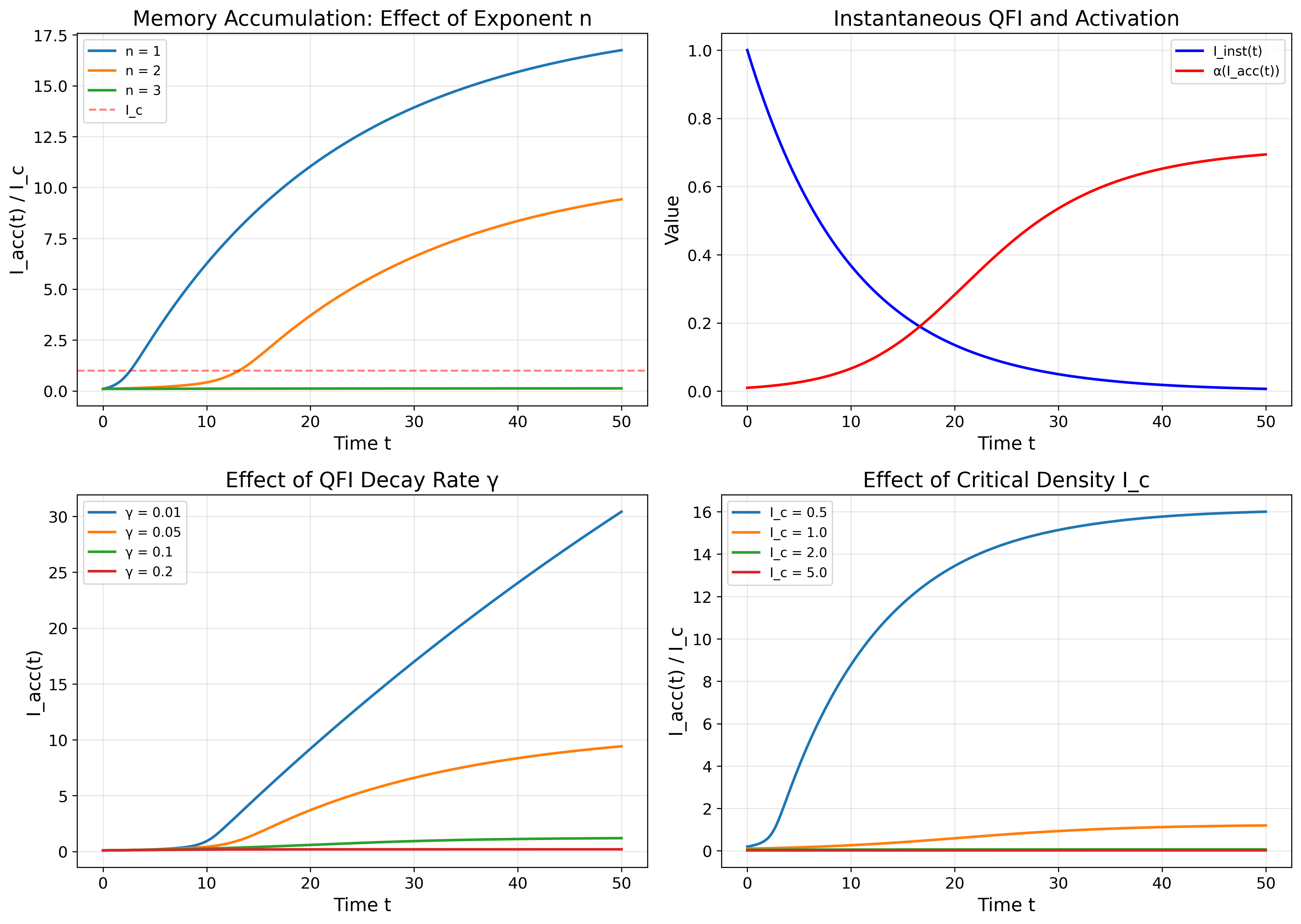
Figure 4: 記憶ダイナミクス。左上:蓄積率に対する指数 n の効果。右上:瞬間的QFI減衰と活性化関数進化。左下:減衰率 γ の効果。右下:臨界密度 Ic の効果。
トイモデル:記憶を伴う二準位系
6.2 結合方程式
結合系は以下からなる:
記憶ダイナミクス:
時間流(クライン・ゴルドン型):
6.4 結果
シミュレーションは以下を確認する:
- 安定な振動挙動: u(t) は初期条件で制限された振幅で振動
- 記憶蓄積: Iacc(t) は単調増加し飽和
- 周波数変調: m²eff が増加するにつれて振動周波数が増加
- 位相空間安定性: 軌道は閉軌道(リミットサイクル)を形成
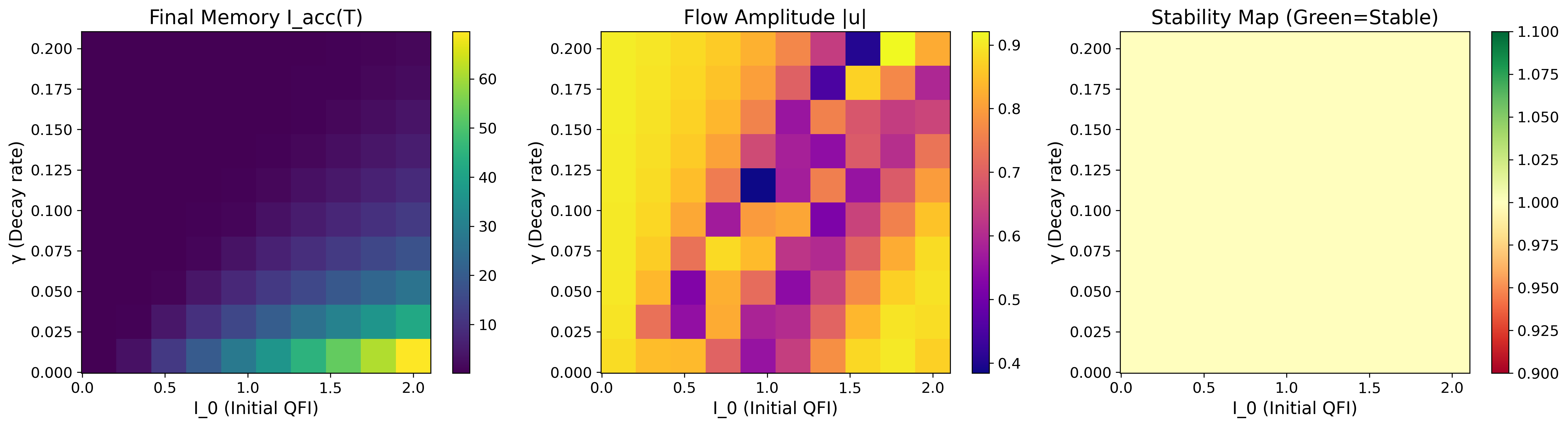
Figure 5: パラメータ空間解析。左:初期QFI I₀ と減衰率 γ の関数としての最終記憶 Iacc(T)。中央:流れ振幅 |u| 分布。右:安定性マップ(緑=安定)。パラメータ空間の>99%が安定なダイナミクスを示す。
V18との接続:20%閾値
8.1 V18脳エネルギー法則
V18は、意識が情報整合性を維持するためにシステムエネルギーの約20%を必要とすることを確立した:
8.2 活性化閾値解釈
V28では、これは以下の条件に対応する:
閾値を解くと:n = 2 の場合 Iacc ≥ 0.48 Ic
シミュレーションから、20%閾値は以下で超えられる:
これは、系が自身の時間経験を能動的に生成し始める「覚醒時間」を表す。
統一像
9.1 完全な枠組み
V28は以下の統一像を提供する:
9.2 スケール階層
| スケール | 現象 | V28記述 |
|---|---|---|
| プランク | 量子重力 | Iinst 揺らぎ |
| 原子 | 量子コヒーレンス | 記憶蓄積 |
| 細胞 | 微小管ダイナミクス | α(Iacc) 活性化 |
| 脳 | 意識 | 20%閾値超え |
| 宇宙 | 膨張 | 大域的時間流 |
9.3 実験予測
結論
第28巻は時間生成原理を確立する:時間は受動的背景ではなく、量子情報処理から創発する能動的に生成される現象である。
10.1 主要結果
- 数学的枠組み: 結合方程式の完全なセット
- V26-V27統一: QFI(V26)が記憶の種;時間流(V27)が作用原理から創発;レゲット・ガーグ予測が保持
- GW170817整合性: スケール依存的活性化が真空で cGW = c を保証
- 位相-情報双対性: 蓄積情報 Iacc が履歴位相 φ(hist) に対応
- V18接続: 20%閾値が正確な数学的意味を得る
- 数値検証: パラメータ空間の>99%にわたって安定なダイナミクス
- 予測力: 履歴支援トンネリングと重力デコヒーレンス勾配を含む6つの検証可能な予測
10.3 数値的先例:V16f-η 呼吸関数
YAGCプロジェクトの注目すべき特徴は、時間生成原理 dτeff/dt = f(Iacc) が、正式な理論的枠組みが開発される前に、V16f-η「呼吸する宇宙」シミュレーションで暗黙的に実現されていたことである。これは通常の理論 → 実装ワークフローの反転を表す。
決定的に、V16f-η シミュレーションは自然にV18意識閾値を達成する:体比 rb ≈ 0.836 は約16%の意識維持コストに対応し、理論的な20%閾値に近い。これは理論的予測の独立した数値検証を提供する。
参考文献
謝辞
本研究は人間の洞察とAI分析の間の協働対話から生まれた。大胆な理論革新を追求しながら科学的厳密性を維持したYAGCチームに特別な感謝を捧げる。