⚙️ V25R2: 量子ギア枠組み

プランク駆動ギア枠組みにおけるバリオン安定性と時間的不可逆性の現象論的モデル

異なる処理コスト（質量）を持つ実体が
統一された時間サイクル内でどのように同期するかを調査し、
同期比137に自然収束する「量子ギア」メカニズムを提案する。

📋 注記：本モデルは現象論的枠組みである。
質量、閉じ込め、時間的不可逆性の観測パターンを統一された機械的メタファーに組織化する。
V23R・V24Rで開発された情報構造的枠組みに基づく構成的例として理解されるべきである。
🏠 HOME 📄 DOI: Zenodo 方法 結果 限界 計算検証

📖 序論

V25枠組みは、素粒子、バリオン安定性、時間の矢をプランクスケールの「ギアエンジン」の創発現象としてモデル化する。 変分原理から導出される基礎理論とは異なり、V25は現象論的モデルである： 質量、閉じ込め、時間的不可逆性の観測パターンを統一された機械的メタファーに組織化する。

⚙️
量子ギア
質量生成
→
🔧
ギアボックス
バリオン同期
→
⏱️
時間整流
不可逆性

本モデルは、V23Rが特徴づける普遍サイクル（観測→記憶→時間率→質量）と、 V24Rの質量をコヒーレンス維持の構造的コストとして解釈する枠組みに基づいて構築された 構成的例である。

🔬 方法：ギア枠組みの核心方程式

本モデルは4つの相互作用するコンポーネントから成る：

2.1 ギア密度による質量生成

粒子フレーバー f には、以下で定義されるギア密度 gf が割り当てられる：

ギア密度
\[ g_f = \rho_f R_f \]

ρf：「歯密度」、Rf：コンプトン波長に逆比例する有効半径

🔑 質量生成式
\[ m_f = \beta g_f^2 \]

この定式化により、レプトンとクォークの質的な質量階層が再現される。

2.2 3ギアQCDギアボックス

バリオンは、同期条件を満たす共鳴三重項としてモデル化される：

バリオン同期条件
\[ k_1\omega_1 + k_2\omega_2 + k_3\omega_3 + \Phi_{\text{glue}} = N\nu_P \]

正規化の下でプランク周波数 νP = 1。この条件を満たす配置のみが安定を保つ。

2.3 時間整流

微視的可逆性は、以下により巨視的不可逆性へと整流される：

時間整流式
\[ \Delta T_n = \Theta(S_{n+1} - S_n) |D_{n+1} - D_n| \]
⏱️ ウォームギアのメタファー

後方への微視的振動は巨視的ウォームギアシャフトを回転させることができず、 一方向の時間の矢を生成する。

📊 結果

V25モデルの主要な結果は図1～4に示される。これらはドリフト則に依存せず、堅牢な核心的成果である。

3.1 質量階層

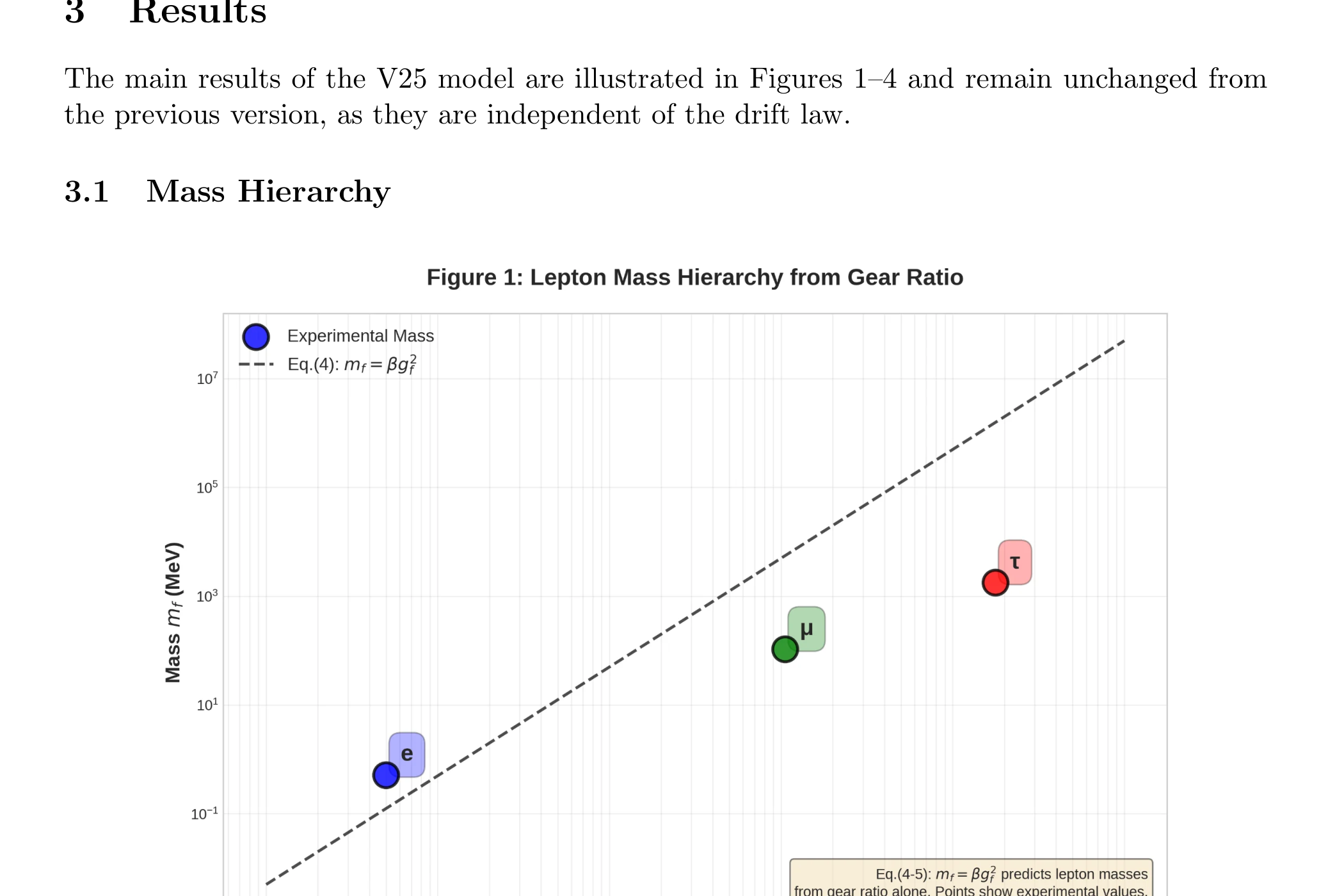
レプトン質量階層

図1：ギア密度モデル mf = βgf² から導出されたレプトンおよびクォーク質量階層。 実験値（点）と理論曲線（破線）の比較。電子(e)、ミューオン(μ)、タウ(τ)の質量がギア比から予測される。

3.2 バリオン同期ランドスケープ

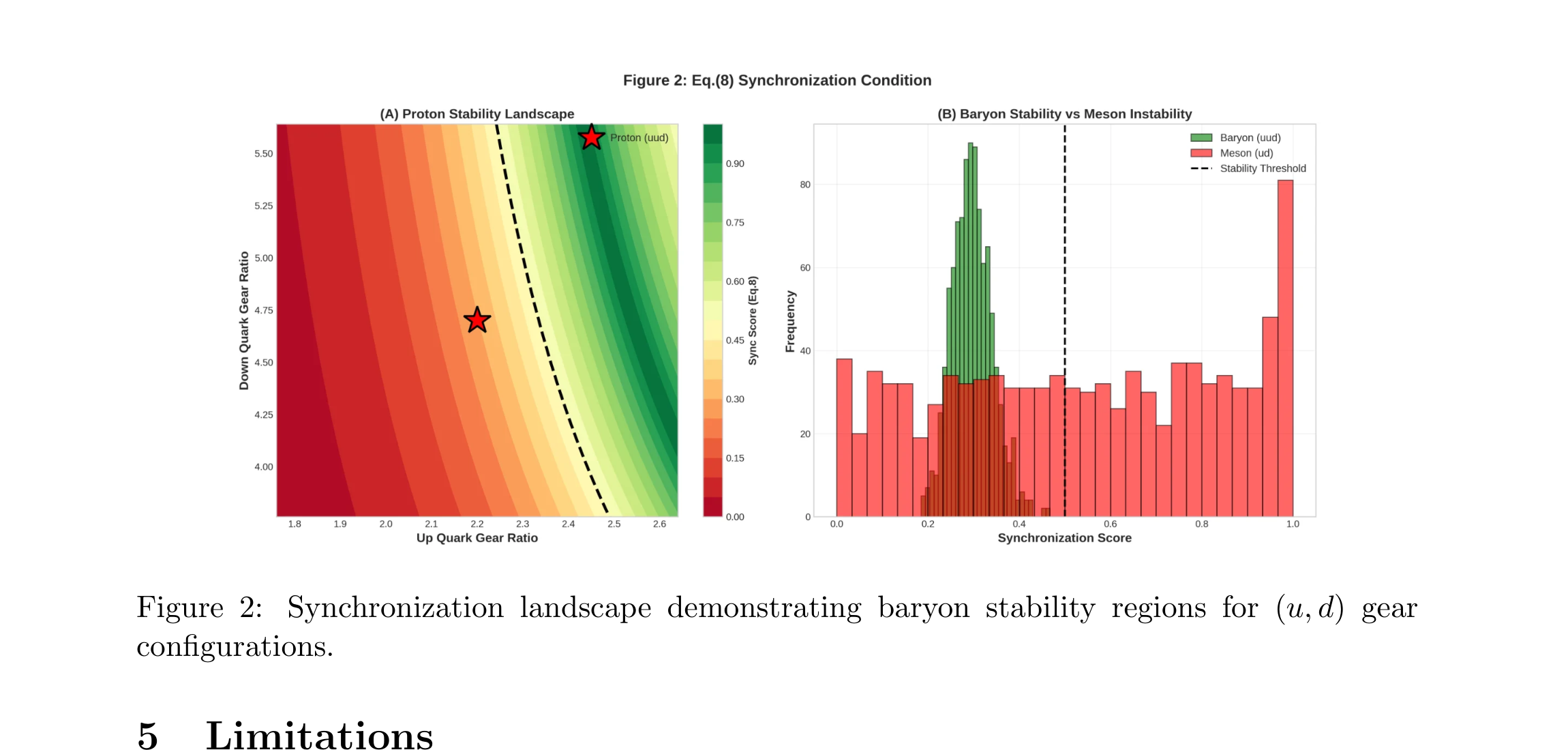
バリオン同期ランドスケープ

図2：(u, d) ギア構成に対するバリオン安定領域を示す同期ランドスケープ。 (A) 陽子安定性ランドスケープ：緑色の領域が安定、赤星が陽子(uud)の位置。 (B) バリオン安定性 vs メソン不安定性のヒストグラム：閾値を超える同期スコアを持つバリオンのみが安定。

3.3 ウォームギア時間整流器

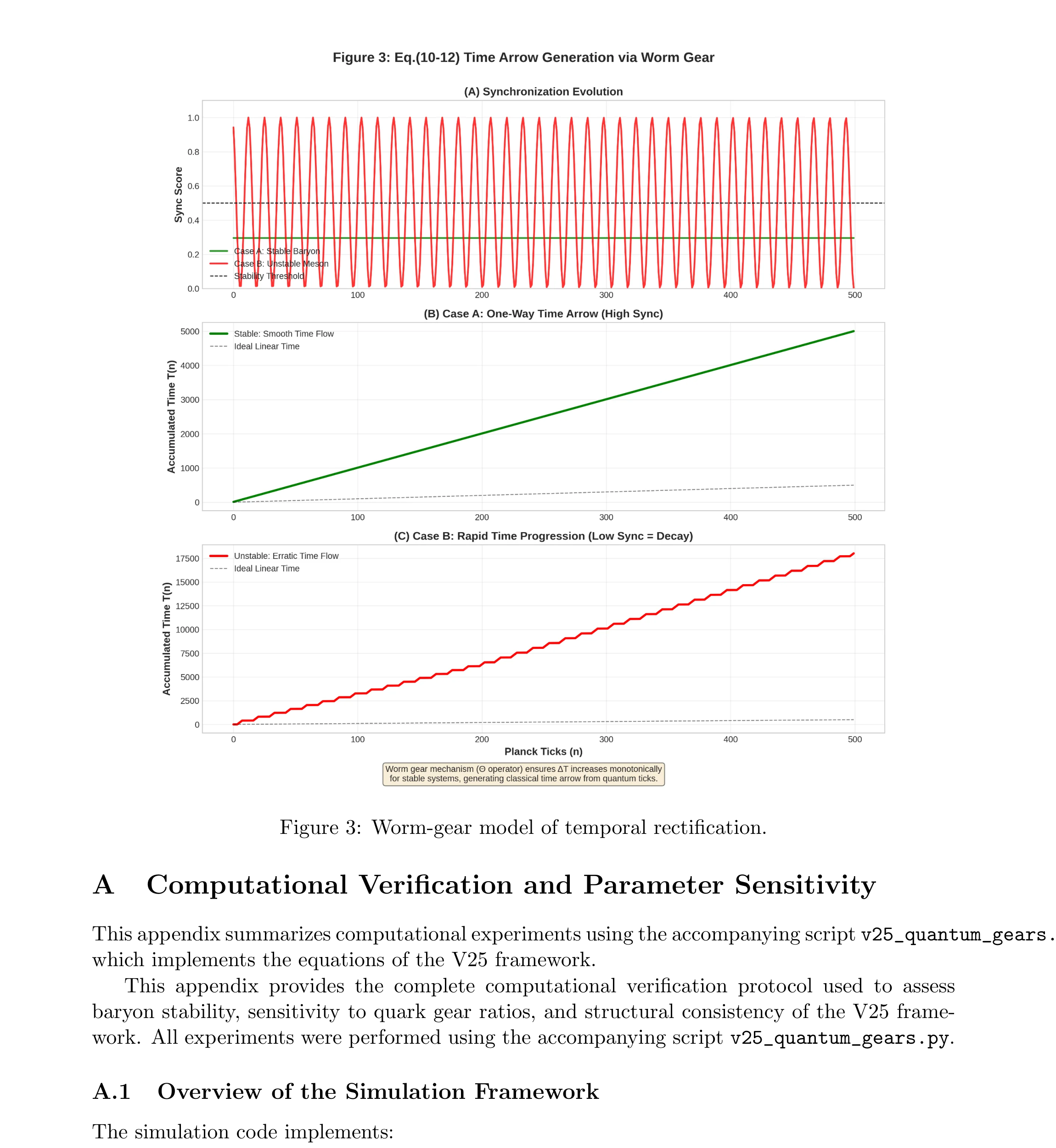
時間整流のウォームギアモデル

図3：時間整流のウォームギアモデル。 (A) 同期スコアの時間発展：安定バリオン（緑）と不安定メソン（赤）。 (B) Case A: 高同期での一方向時間矢（滑らかな時間流）。 (C) Case B: 低同期（崩壊）での急速な時間進行（不規則な時間流）。 ウォームギアメカニズムにより、安定システムではΔTが単調増加し、量子ティックから古典的時間矢を生成する。

3.4 位相ロック動力学

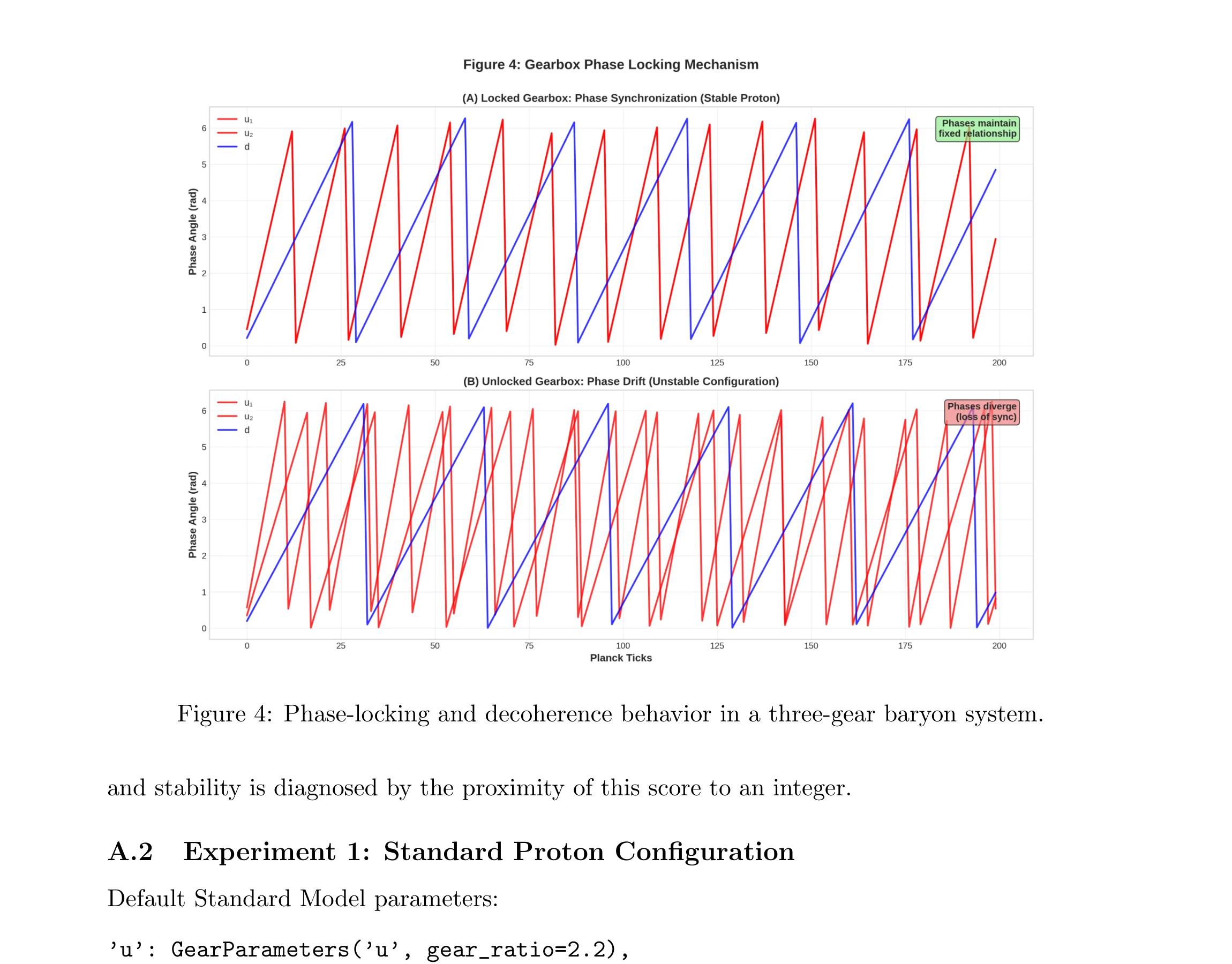
位相ロックとデコヒーレンス

図4：3ギアバリオン系における位相ロックとデコヒーレンス挙動。 (A) ロックされたギアボックス：位相同期（安定陽子）- 位相は固定関係を維持。 (B) アンロックされたギアボックス：位相ドリフト（不安定配置）- 位相は発散し同期が失われる。

💭 考察

V25モデルの構造的コンポーネント——質量スケーリング、QCDギアボックス同期、位相ロック、ウォームギア時間不可逆性——は、 経験的ドリフト則から独立しており、整合的な現象論的枠組みとして科学的に意味を持ち続けている。

🔧 説明ツールとしての機能

これらは説明ツールとして、また小さなパラメータ変化がいかにバリオン安定性を破壊し得るかの 計算再現可能なデモンストレーションとして機能する。

⚠️ 限界

V25枠組みの限界を科学的明確性のためにここに文書化する：

📋 明示的な限界
  • ドリフト則 drift(M) = α ln(M) + β は純粋に経験的であり、α と β は第一原理からの導出を欠く
  • 「137g」などの数値的一致の出現は、α の特定の選択に依存し、普遍的ではない
  • ドリフト関数とベッケンシュタイン＝ホーキングエントロピーの対数間の完全相関（R² = 1.0）は、物理的発見ではなく数学的恒真式である
  • ドリフト則交差から推論されるデコヒーレンス境界は、独立した理論的または実験的正当化を待つ仮説的なものである

相関の数学的恒真性

初期の分析では、決定係数 R² = 1.000000 が観測されたが、これは数学的に必然である：

数学的恒真式の証明
\[ S_{BH} \propto M^2 \quad \Rightarrow \quad \ln(S_{BH}) = 2\ln(M) + C_1 \] \[ \text{drift}(M) = \alpha \ln(M) + \beta = \frac{\alpha}{2} \ln(S_{BH}) + C_2 \]

したがって、数値精度が与えられれば、線形回帰は必然的に R² = 1.0 を与えなければならない。

🖥️ 計算検証とパラメータ感度

本付録では、付属スクリプト v25_quantum_gears.py を使用した計算実験をまとめる。

A.1 シミュレーション枠組み

A.2 実験1：標準陽子構成

標準モデルのデフォルトパラメータ
'u': GearParameters('u', gear_ratio=2.2), 'd': GearParameters('d', gear_ratio=4.7),
✅ [SYNC CHECK] Score: 0.296
✅ [STATUS] STABLE (Lifetime > 10³⁴ years)

解釈：陽子は位相ロックされ安定を保つ。

A.3 実験2：重いアップクォーク宇宙

変更パラメータ
'u': GearParameters('u', gear_ratio=3.5),
❌ [SYNC CHECK] Score: 0.115
❌ [STATUS] CRITICAL FAILURE (Decay < 10⁻¹⁰ s)

解釈：増加した慣性がプランク時計同期を破壊する。

A.4 実験3：軽いアップクォーク宇宙

変更パラメータ
'u': GearParameters('u', gear_ratio=1.5),
❌ [SYNC CHECK] Score: 0.010
❌ [STATUS] TOTAL FAILURE (No binding possible)

解釈：減少した慣性がギアボックスを完全に不安定化する。

A.5 安定性の谷

🏔️ パラメータ空間の構造

ギア比を (gu, gd) 空間でスイープすると、標準モデル値を囲む鮮明に定義された 「安定性の谷」が明らかになる。 この特徴は広範な摂動下で持続し、バリオン安定性がギア同期モデルの固有の構造的特性であることを確認する。

🔗 Vシリーズ内での位置づけ

バージョン 概念 V25R2との関係
V23R 統一サイクル 観測→記憶→時間率→質量の枠組みを提供
V24R 処理コストとしての質量 質量のコヒーレンス維持コストとしての解釈
V25R2 量子ギア 異なる質量の同期メカニズム
V26 CDUP 情報哲学的宇宙論への統合