⚛️ V24R: 慣性質量を構造的処理コストとして

情報哲学的宇宙論（YAGCプロジェクト）の枠組み内で

慣性質量は物理的原始量ではなく、
状態更新時に情報的自己整合性を維持するために必要な
処理コストの顕現である。

📋 注記：本文書は現象論的・構造的枠組みを提示する。
ここで導入される方程式は概念的テンプレートであり、
場の量子論や一般相対性理論から導出された物理法則として提案されるものではない。
🏠 HOME 📄 DOI: Zenodo 慣性の必然性 処理コスト 等価原理 予測と限界

📖 序論

V23Rは、宇宙が離散的な情報サイクルを通じて進化することを確立した：

統一情報サイクル（V23R）
\[ O_t \to \sigma(I_t) \to \rho_{\text{mem}}(t) \to f(t) \to B(t) \to \text{Meta-}r_b \to O_{t+1} \]

V24Rは重要な問いを提起する：

❓ 中心的問い

システムが位置を変えるとき、このサイクルをコヒーレントに保つコストとは何か？

このコストを我々は慣性質量と呼ぶ。

🔑 構造的コスト汎関数
\[ m = \eta \frac{\nu_p}{c^2} \int_\Omega |\nabla D(x)|^2 \, d^3x \]
質量 = 情報多様体全体での歪みパターン更新のコスト

⚡ 慣性の必然性

なぜ慣性は存在しなければならないか

💡 構造的必然性

情報構造を更新するコストがゼロであれば、物体は任意に速く状態を変化させることができ、 因果秩序と解釈可能性を破壊してしまう。したがって慣性は構造的に必然である。

抵抗の根源としての記憶密度

高い記憶密度 ρmem は以下を意味する：

したがって、加速への抵抗は自然に創発する。

⚙️ 構造的処理コストとしての質量

我々は構造的コスト汎関数を、運動時のコヒーレンス維持の情報的負担を計算するものとして再解釈する。

歪み場 D(x)

歪み場は真空基底状態からの局所的逸脱を表す。 プランクティックレベルでの相互作用がランダムウォーク動力学を通じて質量階層を生成し、湯川結合と接続する。

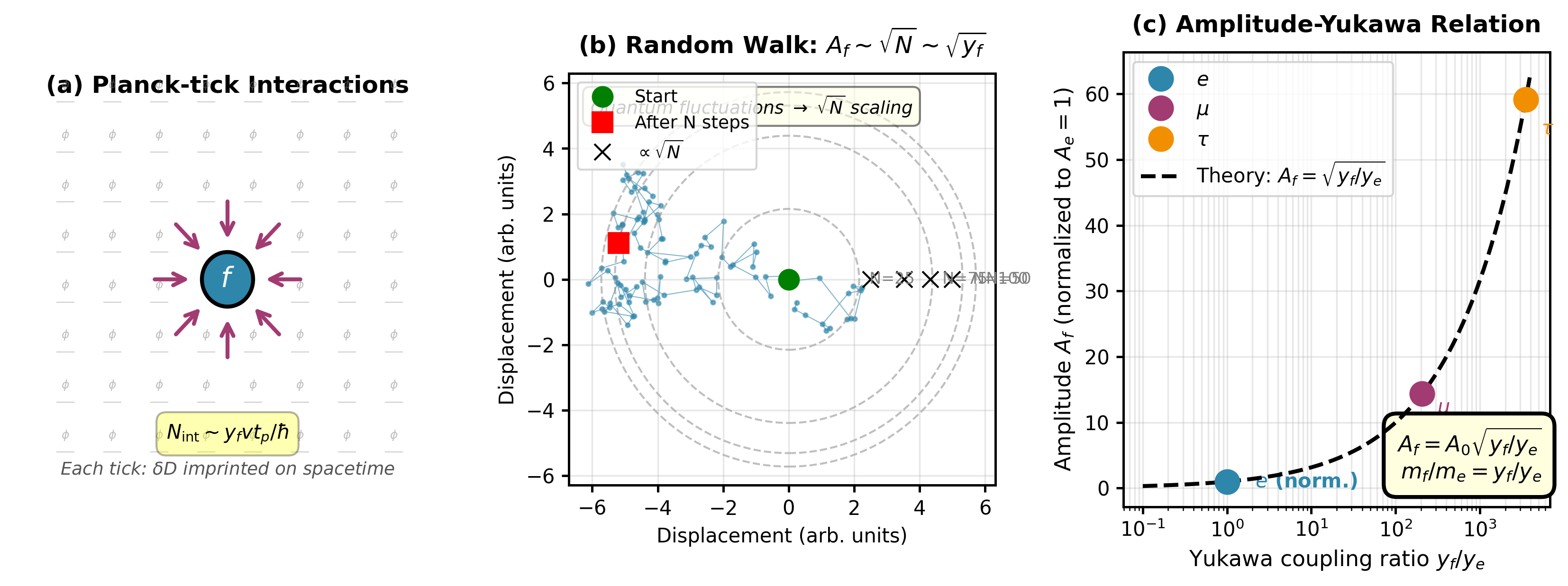
プランクティック相互作用と質量生成

図1：プランクティック相互作用と質量生成。 (a) 離散的プランクティック刻印の概念図。 (b) 振幅スケーリング Af ∼ √N を生成するランダムウォーク動力学。 (c) レプトン質量比を示す振幅-湯川関係。 重要な注記：湯川結合 yf は導出量ではなく経験的入力である。

勾配項の解釈

|∇D| の意味

大きな |∇D| は、空間更新時により大きな構造的調整が必要であることを意味する。

⚠️ 処理コストについての明確化

「処理コスト」という用語は、文字通りの計算回数ではなく情報的メタファーである。 積分は、状態遷移時の自己整合性強制の構造的影響を定量化するものであり、 自然によって実行される物理的操作の数ではない。

⚖️ 等価原理の再解釈

重力質量（V17Rの記憶密度から）と慣性質量（ここでの処理コスト）は同じ情報的起源を共有する。 したがって、それらの等価性は偶然ではなく構造的である。

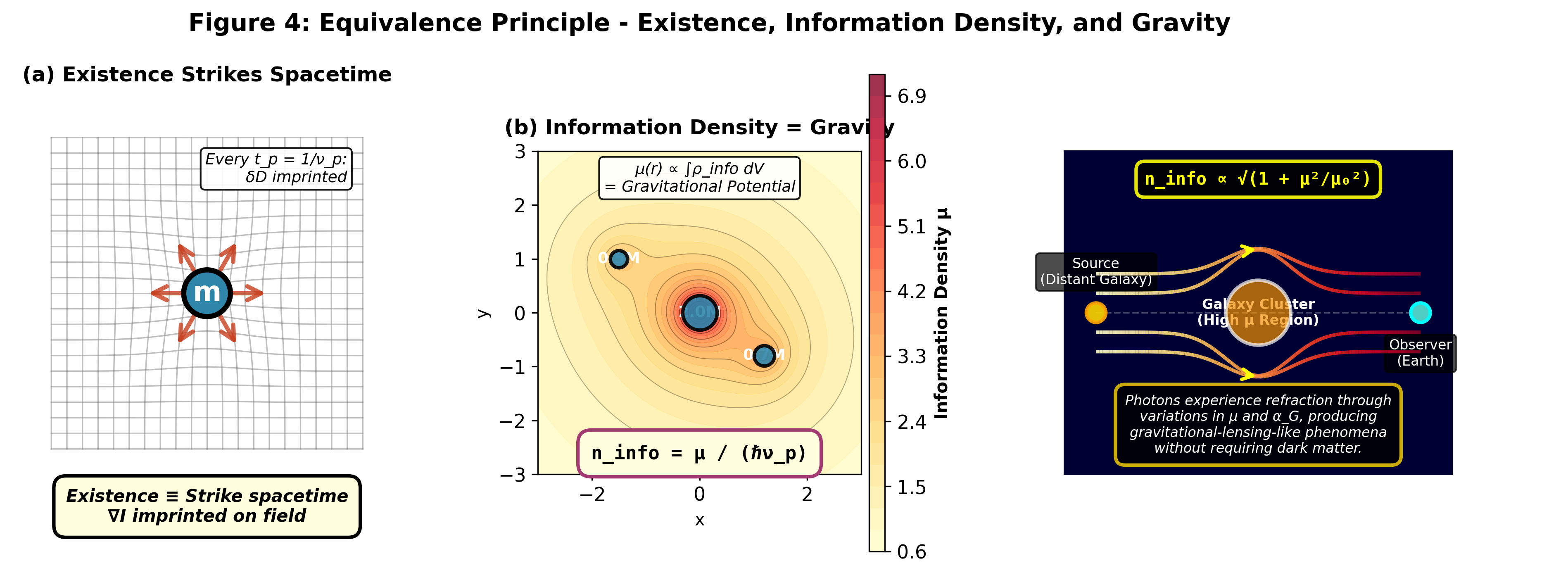
等価原理：情報構造的解釈

図2：等価原理：情報構造的解釈。 (a) 各プランクティックは情報多様体に歪み δD を刻印する。 (b) 情報密度 μ = ρmem/νp は重力ポテンシャルと相関する。 (c) 情報密度変動を通じた重力レンズの再解釈。 注意：この図は等価原理理解のための概念的枠組みを表す。

記憶粘性としての重力の弱さ

重力の極端な弱さ（αG ≈ 10−39）は、記憶蓄積の低効率係数として再解釈できる。

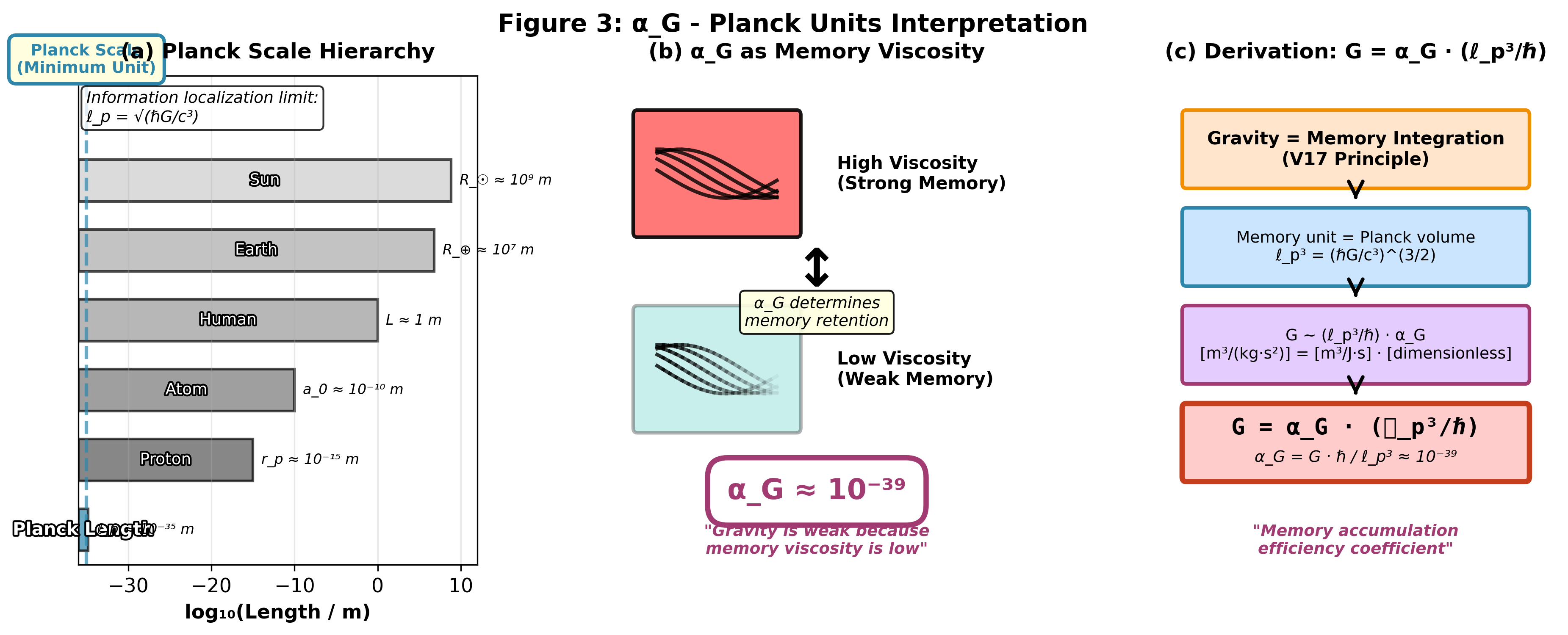
重力の弱さと記憶粘性

図3：重力の弱さと記憶粘性。 (a) 基本スケールから巨視的スケールまでの広大な範囲を示すプランクスケール階層。 (b) 情報が重力効果にどれだけ効率的に蓄積するかを決定するものとしてのαGの解釈。 (c) 次元解析：G = αG · (ℓp3/ℏ)。 注記：この解釈は重力の弱さに関する構造的視点を提供するが、第一原理からのαGの導出を構成するものではない。

⏱️ 時間率と量子ギア

高い記憶密度は時間率を遅くする：

有効時間率（V19R）
\[ f(t) = f_p \cdot \frac{r_b}{(1 + \alpha \rho_{\text{mem}}) \cdot \sigma_\tau} \]
🔗 V25との接続

これはV25における量子ギア同期を安定化させる。 時間率のコヒーレンスが量子的安定性を保証する。

📊 予測と限界

この枠組みは、なぜ質量が構造的歪みと相関するかを説明するが、 標準モデルのパラメータを第一原理から予測するものではない。

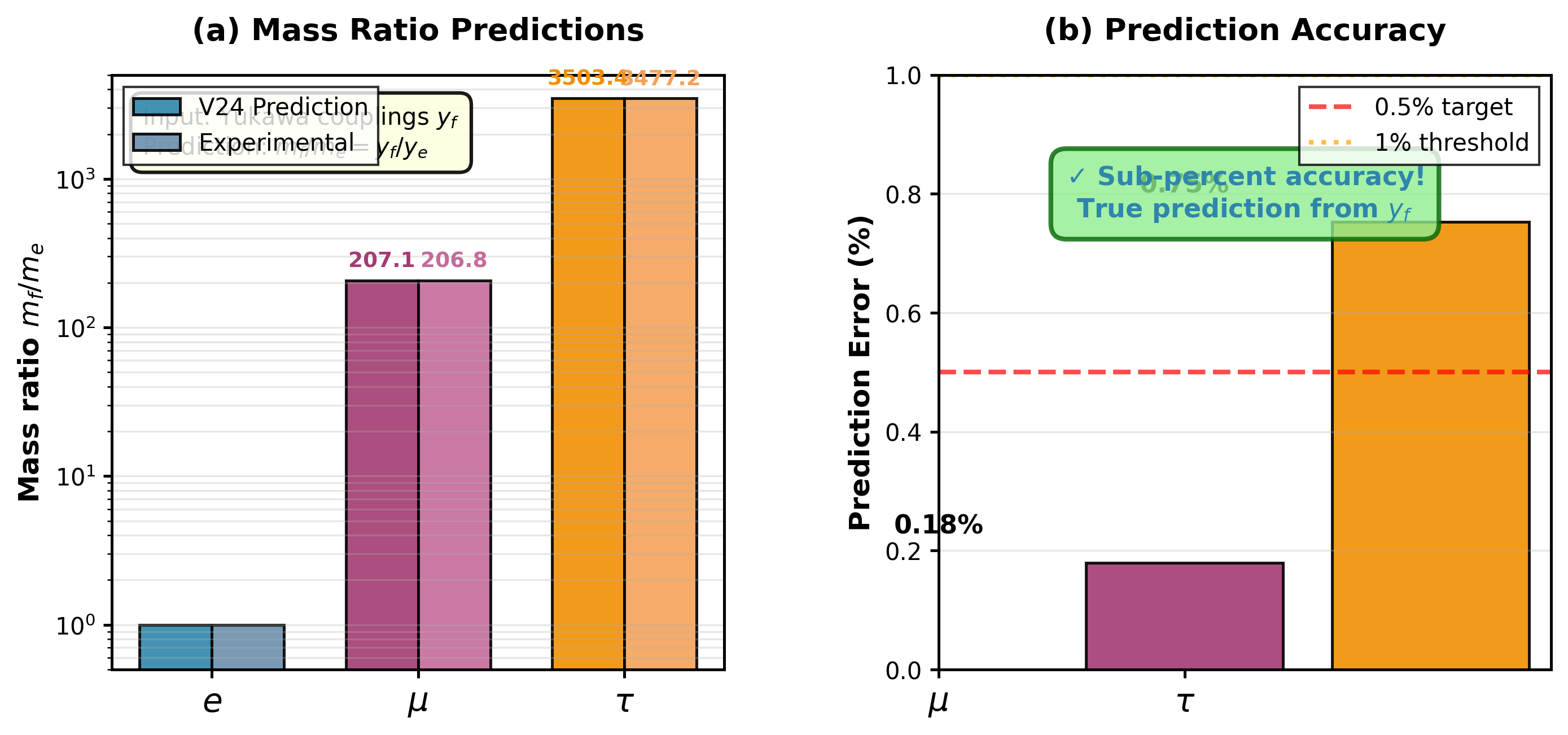
質量比整合性チェック

図4：質量比整合性チェック。 (a) 枠組みの結果と実験値の比較。 (b) サブパーセントの一致を示す精度メトリクス。 重要な限界：これらの結果は経験的湯川結合 yf/ye を入力パラメータとして使用している。

⚠️ 構造的循環性に関する重要な注記

湯川結合 yf は導出量ではなく経験的入力である。 したがって、yf を含む見かけ上の「予測」は独立した導出ではなく構造的再解釈である。

レプトン V24予測 実験値 誤差
電子 (e) 1.0 1.0 —（基準）
ミューオン (μ) 207.1 206.8 0.18%
タウ (τ) 3503.8 3477.2 0.76%

❓ 未解決問題

🔬 今後の研究課題
  • η を第一原理から何が決定するか？
  • 複合粒子に対して D(x) を計算できるか？
  • 質量のない粒子にどう拡張するか？
  • 湯川結合をより深い情報構造的原理から導出できるか？
  • 連鎖「ISN → 湯川 → 質量」を解釈的ではなく予測的にできるか？

📝 結論

V24Rは質量を情報的コヒーレンスに必要な構造的処理コストとして再解釈する。 これはV17R〜V26および整合性駆動宇宙原理と自然に統合される。

✅ 成果

この枠組みは内的整合性を成功裏に実証する： 経験的湯川結合が与えられれば、整合的な構造的メカニズムを通じて正しい質量階層を生成する。

⚠️ 現在の限界

主要な入力パラメータが経験的に決定されたままであるため、まだ真の予測力を達成していない。 今後の研究では、情報構造的必然性（ISN）が湯川結合を制約できるかどうか、 あるいはこれらが我々の宇宙についての還元不可能な経験的事実を表すかどうかに取り組まなければならない。

🔗 Vシリーズ内での位置づけ

バージョン 概念 V24Rとの関係
V17R 記憶としての重力 重力質量の起源
V19R 時間率 質量による時間の遅延
V23R 統一サイクル コヒーレンス維持の文脈
V24R 慣性質量 処理コストとしての質量
V25 量子ギア 時間率による安定化
V26 CDUP 整合性駆動の原理