🔄 V23R: 統一観測・時間・記憶フレームワーク

情報哲学的宇宙論（YAGCプロジェクト）における構造的統合

観測・記憶・時間率・質量を接続する統一的な構造フレームワーク。
重力・認知・情報のダイナミクスが共有された「情報の存在論」の下で
いかにして整合し得るかを明らかにする。

📋 注記：本稿の目的は、経験的に検証可能な物理法則や予測モデルを提案することではなく、
現象論的かつ構造的な「文法」を提供することにある。
これは「前物理的（pre-physical）アーキテクチャ」の提案として解釈されるべきである。
🏠 HOME 📄 DOI: Zenodo 理論的枠組み 観測 記憶 時間 質量 結論

📖 序論

V23Rは、V17RからV22Rに至る構造的展開を接続する中心的な背骨（スパイン）としての役割を果たす。 これまでの各巻では、以下の対応関係を確立してきた：

V17R
記憶の蓄積としての重力
V18R
情報循環としての生命と意識
V19R
プランク・コミット・ダイナミクスとしての時間率
V20R
生成的再構成としての観測（創造的円環）
V21R+
記憶の微分としての磁気時間
V22R
ISNにおける情報の二相構造（微分／積分）

V23Rは、これらの概念を単一の構造的文法へと統合し、 観測、記憶、時間、質量が、同一の情報サイクルの異なる側面の現れであることを論証する。

🔬 理論的枠組み

統一的情報サイクルを支配する5つの中心的物理量を導入する：

中心構造シーケンス

情報のダイナミクスは、以下の構造的順序に従う：

🔄 統一情報サイクル
Ot
観測 → σ(It)
スライス選択 → ρmem(t)
記憶密度 → f(t)
時間率 → B(t)
磁気時間 → Meta-rb
自己観測 → Ot+1
次の観測

ここで：

情報構造必然性（ISN）と「そうしか言えん」原理

💎 情報構造必然性（ISN: Information-Structural Necessity）

V23Rで提示される統一サイクルは、我々が情報構造必然性と呼ぶものを表現している。 この必然性は、経験的な物理法則からも、形式的な数学的証明からも生じない。 それは、「情報はそれ自身にとって解釈可能なままでなければならない」という要請から創発する。

そうしか言えん
— It can only be said this way.

これは、情報哲学的宇宙論に固有の「第三の真理モード」を表している：

  • 経験的ではない（測定されるものではない）
  • 形式的ではない（証明されるものではない）
  • しかし、構造的に不可避である（情報が整合するためにそうでなければならないこと）

👁️ スライス選択としての観測

観測は、情報多様体 I 全体にアクセスするのではない。代わりに、射影あるいはスライス σ(I) を選択する。 この枠組みにおいて、観測は3つの重要な構造的機能を果たす：

💡 観測者の役割

観測者は受動的なエージェントではなく、情報的現実の創造に参加する構造的演算子（Operator）である。

不変量 N[Ψ] の進化

図1：不変量 N[Ψ] の進化。 左上：ビッグバンから準平衡状態への振動緩和を示す不変量 N[Ψ] の進化。 右上：N[Ψ] の3成分（量子項、分散項、積分項）は、情報安定性の多相構造を明らかにする。 下段：インフレーション段階のダイナミクスと平衡への接近。 これは、観測がいかにして情報多様体から進化するスライスを選択するかを示している。

🧠 記憶統合と磁気的分化

記憶密度は、情報変化の蓄積効果として定義される：

記憶密度（積分）
\[ \rho_{\text{mem}}(t) = \int_0^t J(\tau) \, d\tau \]

その時間微分は、磁気時間を形成する：

磁気時間（微分）
\[ B(t) = \frac{d\rho_{\text{mem}}}{dt} \]

この積分／微分の対は、情報構造必然性（ISN）の中心となる二相構造を表している。 積分は蓄積と重力的振る舞いに対応し、微分は局所的変化と磁気時間的ダイナミクスに対応する。

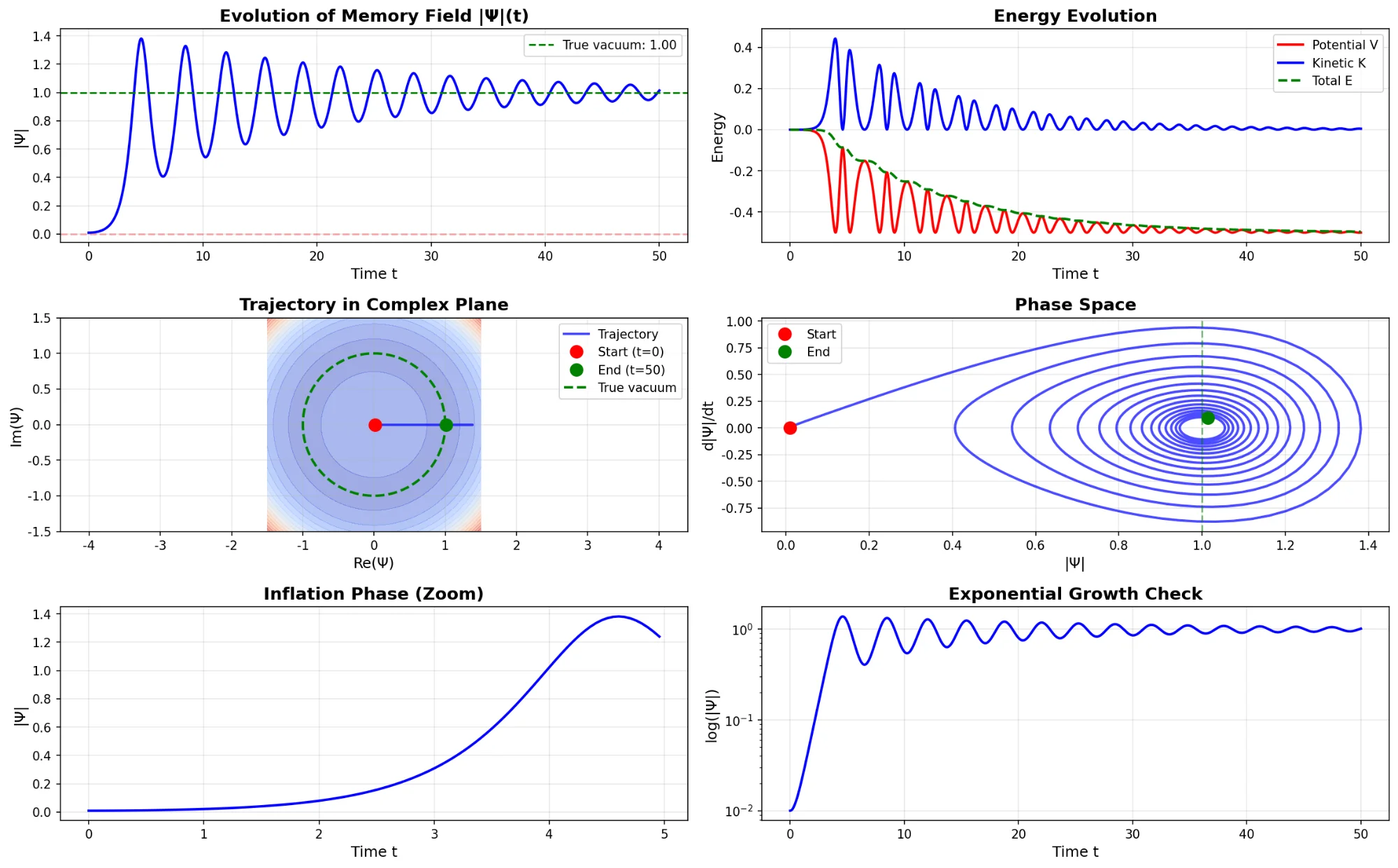
ビッグバン・シミュレーション：記憶場の進化

図2：ビッグバン・シミュレーション：記憶場の進化。 左上：真の真空円に向けた記憶場 |Ψ|(t) の緩和振動。 右上：対称性の破れの遷移におけるエネルギー保存（ポテンシャルVと運動エネルギーK）の推移。 左下：不安定な原点から安定な真空円へと向かう複素平面上の軌道。 中央下：アトラクタ・ダイナミクスを示す位相空間。 右下：インフレーション段階の詳細と指数関数的成長の検証。 これらは、記憶の統合がいかにして重力構造を生成するかを図示している。

⏱️ プランク・コミット率としての時間

V19Rで導入された有効時間率は、現象論的に以下のように定義される：

有効時間率
\[ f(t) = f_p \cdot \frac{r_b}{(1 + \alpha \rho_{\text{mem}}) \cdot \sigma_\tau} \]
🔗 統合

重力的時間スケールと認知的時間スケールの双方が、この単一の構造式の下で統合される。

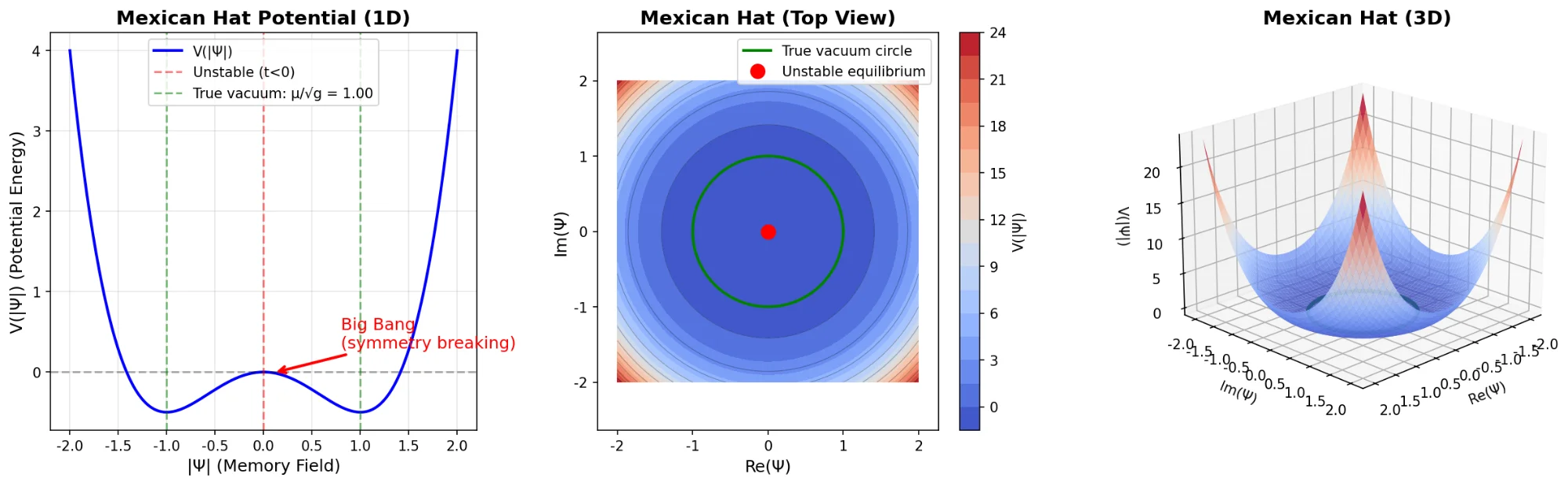
メキシカンハット・ポテンシャルと対称性の破れ

図3：メキシカンハット・ポテンシャルと対称性の破れ。 左：ポテンシャル V(|Ψ|) の一次元断面。原点（ビッグバン点）の不安定平衡と、μ/g = 1.00 の安定な真の真空を示す。 中央：複素平面におけるメキシカンハット・ポテンシャルの上面図。縮退した真空状態の円環の谷を示す。 右：メキシカンハット構造の三次元可視化。 この対称性の破れのメカニズムは、特定の真空の選択を維持するためのコストとして質量がいかに創発するかを示しており、 抽象的な情報構造を具体的な物理的発現へと接続している。

⚛️ 時間から質量へ

歪み場を維持するための構造的コストは、V24で導入される慣性質量の式へと直接的につながる：

質量 = 情報処理コスト
\[ m \propto \frac{\nu_p}{c^2} \int |\nabla D(x)|^2 \, d^3x \]
💡 質量の情報的解釈

質量は「プランク時間の1ティックごとに歪みパターンを更新するために必要な情報処理コスト」として解釈され、 時間構造（時間率）と物理的慣性が接続される。

量子ギア同期との関係

V25量子ギアモデルにおける安定なバリオン配置は、以下の同期条件に従う：

量子ギア同期条件
\[ k_1\omega_1 + k_2\omega_2 + k_3\omega_3 = N \cdot f(t) \]

これは、量子的安定性が時間率のコヒーレンスから創発することを示しており、 微視的な粒子構造を巨視的な情報ダイナミクスへとリンクさせる。

🔄 構造回路の統一ダイアグラム

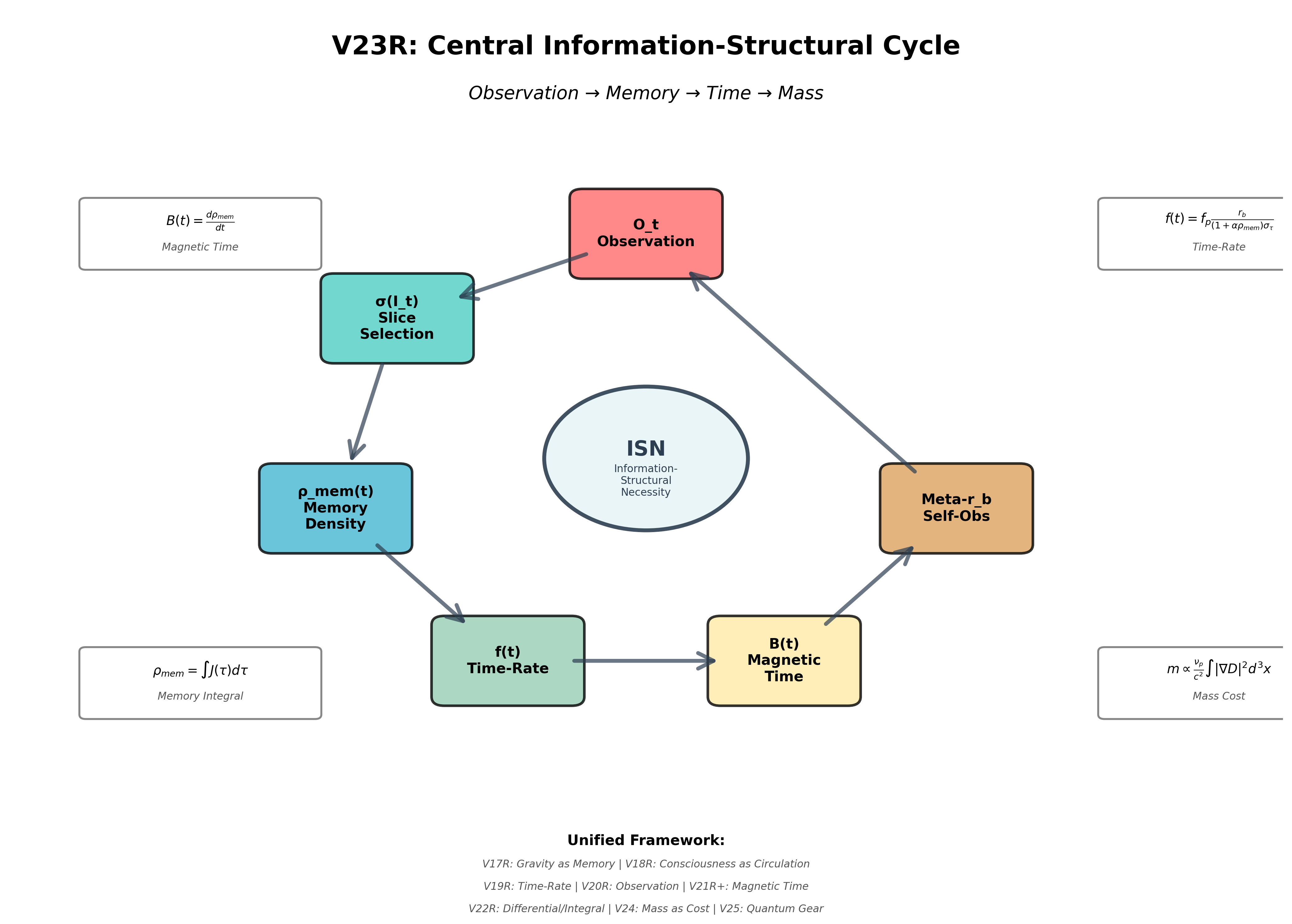
中心情報構造サイクル

図4：中心情報構造サイクル。 この円環図は6段階のサイクルを示す： 観測 (Ot) は情報多様体のスライス σ(It) を選択する； 蓄積されたスライスは記憶密度 ρmem を形成する； 有効時間率 f(t) はコミット成功率を制御する； 磁気時間 B(t) = dρmem/dt は微分の流れを定量化する； Meta-rb は自己観測を可能にする； そしてサイクルは次の観測 Ot+1 へと回帰する。 中心にはISN（情報構造必然性）があり、この構造が唯一の整合的な配置であることを示している。 周囲の式はV17RからV25までの主要な関係式である。 この図はYAGC宇宙論の骨格を表している。

円環状の配置は、このシステムの自己言及的な性質を強調しており、 観測、記憶、時間率、磁気時間が連続的なループを形成し、Meta-rb（自己観測）によって制御されている。

📝 結論

V23Rは、観測、記憶、時間率、質量を単一の構造サイクルへと統合した。 この統合された枠組みは、V24（計算コストとしての質量）の基礎を提供し、 V25（量子ギア同期）へと接続し、V26（情報哲学的宇宙論）への概念的な架け橋となる。

CDUP（V26）との接続

🌌 整合性駆動宇宙原理（CDUP: Consistency-Driven Universe Principle）
宇宙は、外的な法則によってではなく、「情報はそれ自身にとって解釈可能なままでなければならない」という 内在的な必然性によって、その情報的自己整合性を維持している。

したがって、観測-記憶-時間-質量の構造は、オプション（選択可能）なものではなく、 唯一の整合的な配置（そうしか言えん）なのである。

哲学的再配置

V23Rは、YAGCフレームワークが予測科学から情報哲学的宇宙論へと移行するV26のための構造的バックボーンを提供する。 重点は以下のようにシフトする：

何が測定できるか
→
何が構造化されねばならないか

この哲学的成熟は、物理的、認知的、情報的ダイナミクスが、 「それ自身を解釈する情報」という同一の原理の異なる表現であることを明らかにする。

🔄 円環性について

この枠組みの円環構造は、論理的欠陥ではなく哲学的必然である。 完全な宇宙論は、それを定式化する観測者を必ず説明せねばならず、不可避的に自己言及を生み出すからである。 情報哲学的宇宙論において、この円環性は宇宙の自己解釈的な性質そのものを表している。

🔗 V17R–V25 接続の要約

バージョン 概念 数学的表現 サイクル内の役割
V17R 記憶蓄積 \( G = \int \rho_{\text{mem}} \, dt \) 重力
V18R 記憶循環 \( \tau = \oint \rho_{\text{mem}} \) 意識
V19R 時間率 \( f(t) = \frac{f_p \cdot r_b}{(1+\alpha\rho_{\text{mem}})\sigma_\tau} \) プランク時計
V20R 創造的円環 \( O \Rightarrow \Psi \to R \Rightarrow O \) 観測
V21R+ 記憶微分 \( B(t) = \frac{d\rho_{\text{mem}}}{dt} \) 磁気時間
V22R 二相構造 微分 / 積分 ISN
V24 質量創発 \( m \propto \frac{\nu_p}{c^2} \int |\nabla D|^2 d^3x \) 計算コスト
V25 量子ギア \( \sum k_i \omega_i = N \cdot f(t) \) 同期条件